
In a previous blog post, we presented the applications of conjugate heat transfer involving immobile solids. The case of immobile solids simplifies the heat equation to be solved and is often a good approximation to the temperature field. Today, we will complete the description of the physics that account for thermoelastic effects of the material when heat transfer and solid mechanics are coupled.
Material and Spatial Frames
Before going into the physics, we should briefly recall the system of frames used in COMSOL Multiphysics. When geometric nonlinearities are considered, the Solid Mechanics interface makes the distinction between material and spatial frames. The material frame expresses the physical quantities in the coordinates of the initial state \mathbf{X} = (X, Y, Z), while the spatial frame uses the coordinates \mathbf{x} = (x, y, z) of the current state.
The two figures below present the example of a square submitted to compressive strain. The square is ten centimeters long and its bottom-left corner is initially located at (X, Y) = (1~\textrm{cm}, 1~\textrm{cm}). It is then compressed by boundary loads at its left and right sides. This deformation modifies the position of almost all points of the square. For instance, the bottom-left corner moved to a new location (x, y) = (1.54~\textrm{cm}, 0.82~\textrm{cm}).
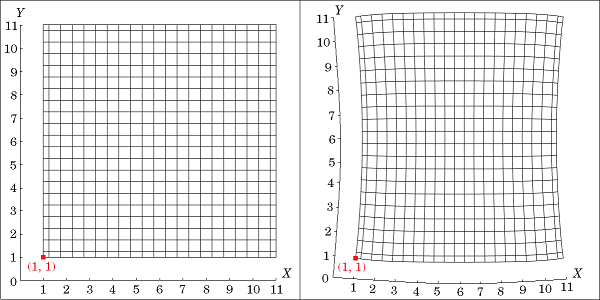
A deformed square represented in material coordinates, initial state on the left and final state on the right.
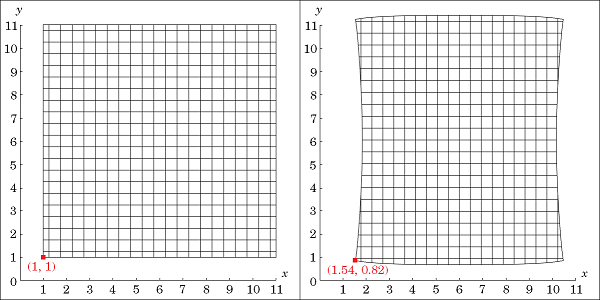
A deformed square represented in spatial coordinates, initial state on the left and final state on the right.
The material coordinates always refer to the same particle in time, which was initially at a given point (X, Y, Z). The momentum equation of Solid Mechanics is formulated in this coordinate system. On the other hand, a point (x, y, z) in spatial coordinates refers to any particle that would be located there at the current state. The heat equation is formulated in this coordinate system.
In these two frames, volume-related physical quantities have different values. For instance, without any mass source, the density in material coordinates remains constant before and after transformation while the density in spatial coordinates changes according to the volume change. Hence, in order to couple an equation formulated on the material frame (structural mechanics) and another equation formulated on the spatial frame (heat transfer), these values need to be properly evaluated on each frame. The following table provides a list of conversions for some thermal physical quantities from spatial to material frame. These conversions involve the deformation gradient \mathbf{F} = {\partial \mathbf{x}} / {\partial \mathbf{X}} and its determinant, J. Both are evaluated using the displacement field computed by the Solid Mechanics interface.
| Quantity | Material | Spatial |
|---|---|---|
| Temperature | T | T |
| Density | \rho_0 | \rho = J^{-1} \rho_0 |
| Thermal conductivity tensor | \bold{k}_0 | \mathbf{k} = J^{-1} \mathbf{F} \mathbf{k}_0 \mathbf{F}^T |
| Thermoelastic damping | W_{\sigma, 0} = \boldsymbol{\alpha} T : \frac{\mathrm{d} \mathbf{S}}{\mathrm{d} t} | W_\sigma = J^{-1} W_{\sigma, 0} |
| Heat source | Q_0 | Q = J^{-1} Q_0 |
Conversion of thermal physical quantities from material to spatial frame.
These conversions also reflect the fact that stress and strain affect the heat transfer by modifying the geometrical configuration (represented in the spatial frame). For example, a stretched boundary is more likely to receive a higher amount of heat by radiation (Q_\mathrm{r} > Q_{\mathrm{r}, 0}), as shown below.
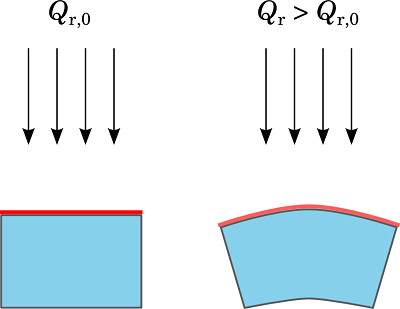
Radiative heat flux received at the top surface of a solid, initial state (left) and after stretching the top surface (right).
Another example, the thermal conductivity expression in the spatial frame, usually using the initial state value \bold{k}_0, involves the quantities \mathbf{F} and J related to solid strain.
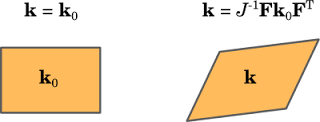
Modification of the thermal conductivity on the spatial frame after deformation of a solid.
Temperature-Dependent Stress and Strain
The equations of Solid Mechanics are defined in the material frame. They relate the displacement, \mathbf{u}, the second Piola-Kirchhoff stress tensor, \mathbf{S}, and the elastic strain tensor, \mathbf{E}_\mathrm{el}, by a linear momentum balance equation and a stress-strain relation:
(1)
(2)
Here, \mathbf{C} is the elasticity tensor, which is often defined from the Young’s modulus and the Poisson coefficient. It may depend on the temperature as it is the case for Carbon Steel 1020.
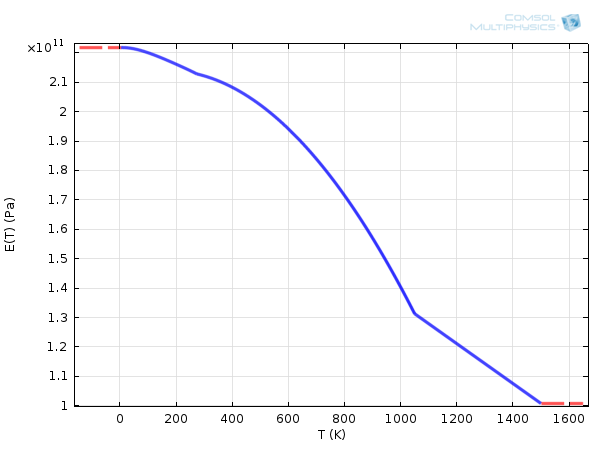
Young’s modulus of Carbon Steel 1020, depending on the temperature.
Without any plastic effects, the elastic strain tensor, \mathbf{E}_\mathrm{el}, carries the temperature dependence via the thermal strain tensor, \mathbf{E}_\mathrm{th}, according to:
(3)
(4)
(5)
The coefficient of thermal expansion, \boldsymbol{\alpha}, characterizes the ability of the material to contract and expand because of temperature variations. It is often scalar but may more generally take a tensor form. The table below shows a list of typical values of isotropic \boldsymbol{\alpha}.
| Material | Coefficient of Thermal Expansion (10-6 K-1) |
|---|---|
| Acrylic plastic | 70 |
| Aluminum | 23 |
| Copper | 17 |
| Nylon | 280 |
| Silica glass | 0.55 |
| Structural steel | 12.3 |
Coefficients of thermal expansion for some materials.
In addition, \boldsymbol{\alpha} can, itself, depend on the temperature as shown by the example below.
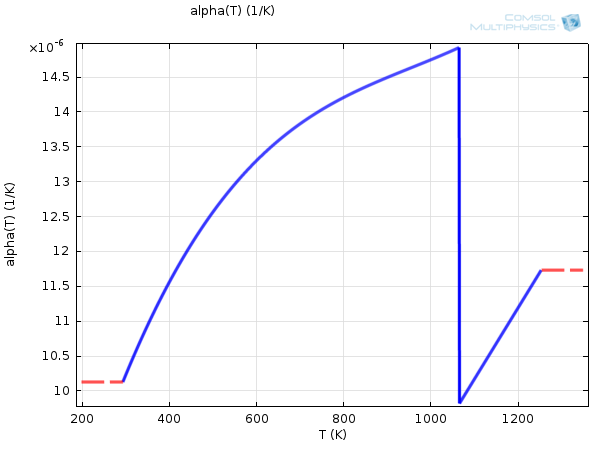
Coefficient of thermal expansion of Carbon Steel 1020, depending on the temperature.
As seen in these examples, the values of \boldsymbol{\alpha} are most often of the order of 10-5 K-1. Hence, for \mathbf{E}_\mathrm{th} to become significant, a high temperature difference from the reference state is necessary. For instance, aluminum needs to reach about 500 K above the reference temperature to show a thermal elongation of only 1.2%.
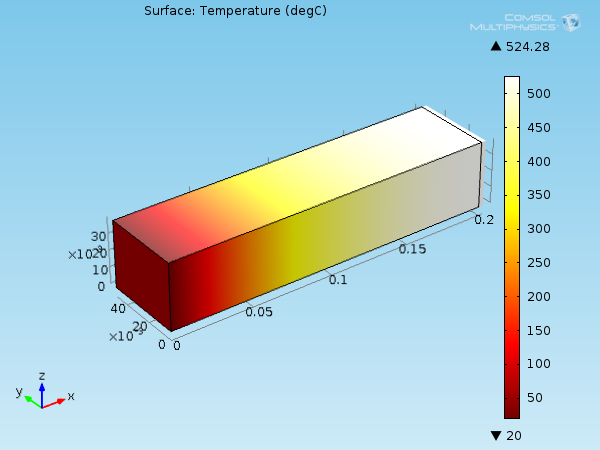
Example of thermal expansion of a constrained aluminum beam heated 500 K, using a deformation scale of 1:1.
Note that in the formulation of Equations (3)-(5), the thermal strain is subtracted from the total strain. This is an appropriate approximation for small strains, which the thermal strains normally are, due to usually low values of \boldsymbol{\alpha}. The more accurate multiplicative formulation, valid for large thermal strains, is shown below but not discussed further. This formulation is used for the hyperelastic materials in COMSOL Multiphysics.
(6)
(7)
(8)
The Heat Equation for Deformed Solids
The heat equation is an energy balance equation deduced from the First Law of Thermodynamics. For solids, it takes the following form when formulated on the spatial frame:
(9)
The coupling term W_\sigma is the heat source due to compression or expansion of the solid and is defined by:
(10)
which, in the case of \boldsymbol{\alpha} being independent from temperature, reduces to:
(11)
Here, \boldsymbol{\alpha} is the same coefficient of thermal expansion as in \mathbf{E}_\mathrm{th}. The low value of \boldsymbol{\alpha}, as seen in the table above, has to be compensated for by high enough values of T {\mathrm{d} \mathbf{S}} / {\mathrm{d} t} to make W_\sigma a significant heat source, that is:
- by a high temperature
- by rapid and high variations of stress
We have now described four key contributions to the multiphysics coupling between Heat Transfer and Solid Mechanics:
- The influence of strain and stress on thermal quantities and boundary heat fluxes in the material or spatial frames
- The temperature dependence of the elasticity matrix
- The temperature dependence of the elastic strain tensor via the thermal strain tensor
- The heat source, W_\sigma, corresponding to thermoelastic damping in the solid
Next, we will illustrate the last two coupling contributions and show how to handle them in COMSOL Multiphysics with a couple of modeling examples.
Example 1: Thermal Stress in a Turbine Stator Blade
My colleague Nicolas previously described in more detail how to model thermal stress in a turbine stator blade. Here, we display only the results in order to show the effects of J_\mathrm{th}. Because this is a steady-state model, the thermoelastic damping, W_\sigma, can be ignored.
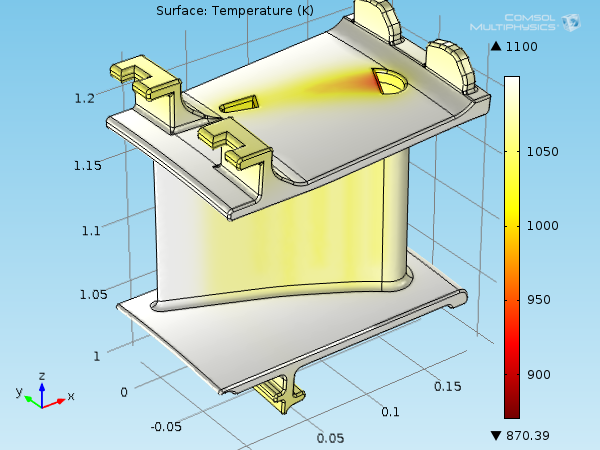
Temperature field on the blade surface, representation in the material frame.
Due to a hot environment, the temperature field shows values between 870 K and 1100 K compared to the reference temperature of 300 K that the shape of the stator blade is initially. Such high temperatures make the material more prone to thermal deformations. The average coefficient of thermal expansion and temperature being around 1.2·10-5 K-1 and 1070 K, \mathbf{E}_\mathrm{th} is around 0.9%.
The volume expansion, due to thermal effects, for large deformations is \Delta V/V_0 = J_\mathrm{th}-1 (where J_\mathrm{th} was introduced in Equation (8)). It is still a good approximation for a small strain, giving an expansion of around 2.80%. In postprocessing, the actual volume expansion is found to be 2.76%.
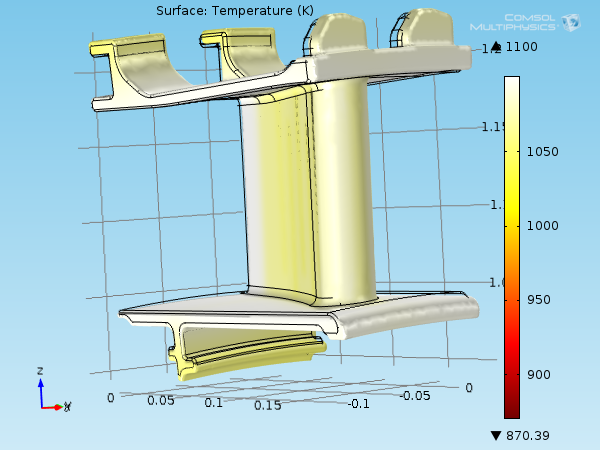
Temperature field and deformation of the stator blade, exaggerated plot with a scale factor of 3 for more visibility.
Example 2: Transient Analysis of a Bracket with Heat Transfer
The Bracket — Transient Analysis model is available both in the Structural Mechanics Module Model Library and the Model Gallery. In this model, the arms of the brackets move according to rapid time-dependent loads. Consequently, small variations of temperature should occur.
The existing model neglects these thermal effects, so we need to add a new Heat Transfer in Solids interface.
Then, we add the two multiphysics features below to couple the Heat Transfer in Solids and Solid Mechanics interfaces:
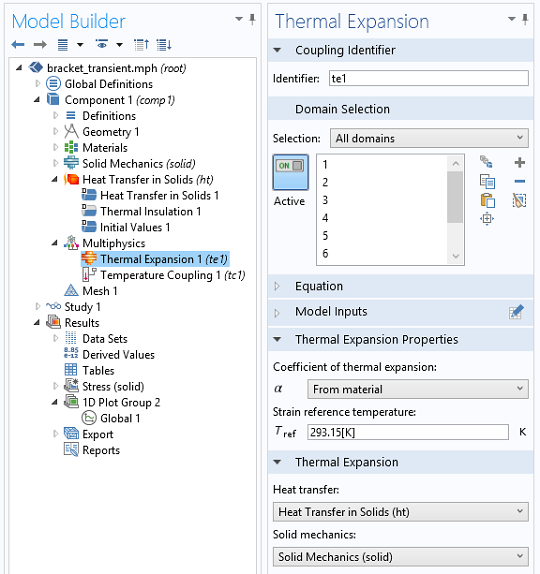
- Thermal Expansion
- This modifies the thermal strain tensor, \mathbf{E}_\mathrm{th}, applied on the whole bracket domain and accounts for the thermoelastic heat source, W_\sigma
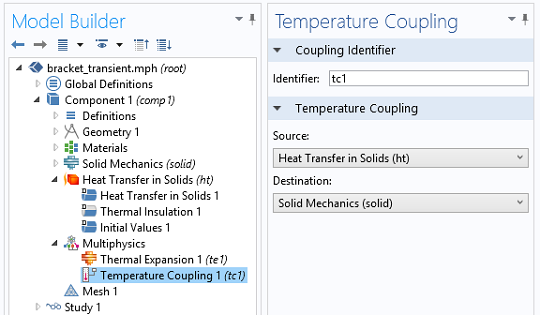
- Temperature Coupling
- This couples the temperature variable computed by the Heat Transfer in Solids interface with the Solids Mechanics interface
The study can also be extended to 30 milliseconds to observe more load periods.
Starting from an isothermal profile of 20°C everywhere, the small temperature variations lead to a negligible thermal strain tensor. The main contribution to thermal effects is now the thermoelastic heat source due to rapid stress variations.
Temperature profile of the bracket over time, exaggerated plot with a scale factor of 10 for more visibility.
Differences of about 0.8 K can be observed between the extreme temperatures in the bracket. The heating and cooling process is, as expected, located at corners where the stress is more important and its variations stronger.
Conclusion
The heat transfer in a deformed solid is numerically computed by solving the heat equation and the momentum balance equation. For practical reasons, we made the distinction between two systems of coordinates:
- The material frame where the equation of motion is formulated
- The spatial frame for the heat equation
Volume-related quantities in both frames have different values and need a conversion from each other, in particular for specific energies and density.
The two governing equations each contain coupling terms that makes the solid motion dependent on the temperature and the heat transfer dependent on the solid deformation. As shown in the previous two examples, COMSOL Multiphysics provides appropriate functionalities to conveniently account for them.
When temperatures remain near the reference state and without too rapid stress variations, these coupling effects are negligible. Otherwise, they shall be added to the formulation on the model.
To delve deeper into this topic, you can download the files related to the models mentioned here and read a couple of related blog posts via the links in the section below.
Further Resources
- Model downloads:
- Previous blog posts:
Editor’s note: This blog post was updated on 7/23/2015 to be consistent with version 5.1 of COMSOL Multiphysics.




Comments (3)
Ashley Emery
January 5, 2016This blog defines the thermal conductivity in the deformed region as k=(1/J)F^T k_0 F
where F=dx/dX
Please check this. My references give k=(1/J) F k_0 F^T which is not the same even for isotropic k_0
Peng Chhay Ung
January 8, 2016Thank you very much for your comment! You are completely right and the formulas have been fixed in this blog post.
Tianyu Yang
June 1, 2021Is there a simple way to convert the deformed solid material frame to heat transfer spatial frame? How can I manipulate these conversion matrices in COMSOL?
Thank you.