
Today, we invite guest blogger Nagi Elabbasi of Veryst Engineering to share the work they performed on simulating wear in COMSOL Multiphysics.
Using the COMSOL Multiphysics® software, we implemented a wear model and validated it by simulating a pin-on-disc wear test. We then used the model to predict wear in an automotive disc brake problem. The results we found showed good agreement with published wear data.
Editor’s note on 12/13/22: At the time when this blog post was written, there was no built-in functionality for computing wear. The Wear feature was introduced in version 5.6 of COMSOL Multiphysics for doing just that.
About Wear
Wear is the process of the gradual removal of material from solid surfaces that are subjected to sliding contact. It is a complex phenomenon that is relevant to many problems involving frictional contact, such as mechanical brakes, seals, metal forming, and orthopedic implants. The rate of wear depends on the properties of the contacting materials and operating conditions.
Archard’s law is a simple but widely used wear law that relates the volume of material removed due to wear W to the normal contact force F_N, sliding distance L_T, material hardness H, and a material-related constant K
In our work, we considered a modified version of Archard’s law:
This modified law relates the wear depth w at any point to the normal contact pressure p_N, magnitude of sliding velocity V_T, and a constant k that is a function of the material and temperature. The wear constant k may be computed from experimental wear data, which is typically in the form of weight loss for a specific contact pressure and velocity.
Wear equations are not directly available in finite element analysis (FEA) codes, although their implementation in COMSOL Multiphysics is straightforward. We incorporated the wear equations within our simulations by defining boundary ordinary differential equations (ODEs) on the destination contact surfaces with the wear depth w as the independent variable. The wear depth w is then used as an offset between contacting surfaces (e.g., brake pad and disc) within the contact formulation in COMSOL Multiphysics. In particular, contact is enforced when the penetration between the contact surfaces is equal to the wear depth w, as shown in image below.
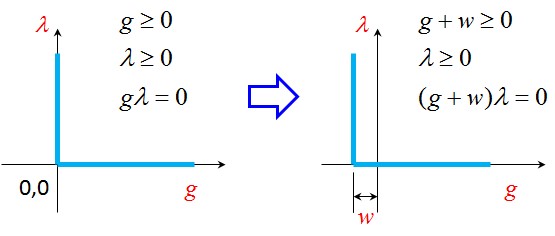
Modification of contact gap calculation: w is the wear depth, g is the gap, and \lambda is the contact pressure.
This wear algorithm is very efficient since it does not involve altering the nodal locations to account for material loss due to wear. It is only suitable, however, for cases where the wear depth is significantly less than the width of the contact surface.
You can enhance this wear algorithm by including more sophisticated effects, such as anisotropic wear behavior, dependence on the mean and deviatoric stresses in the solid (not just the contact pressure), threshold pressure/stress below which no wear occurs, and more. The assumption of small wear depth must still hold for this modeling approach to be accurate.
Simulating a Pin-On-Disc Wear Test
We validated the new, contact-offset-based wear model implementation by simulating a pin-on-disc wear test. Only a small section of the disk is modeled, as shown below.
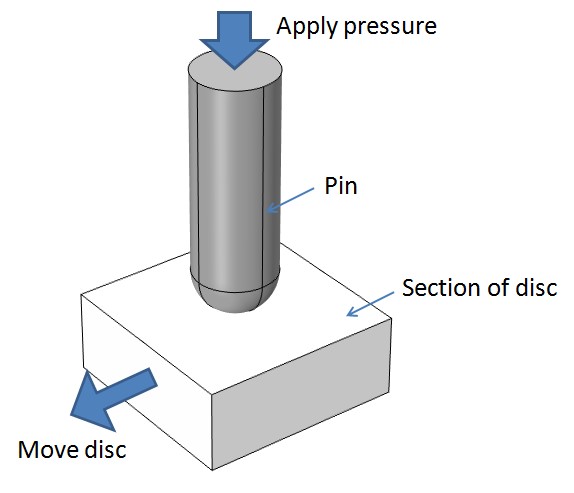
Pin-on-disc wear test model.
The disc in this model is much stiffer than the pin and all the wear is assumed to occur in the pin. A force is applied to the pin, resulting in a circular, Hertzian-type contact pressure distribution. A constant tangential velocity is then applied to the disc. The graph below shows how the wear depth varies radially along the pin at four time instances. The total volume loss, calculated as the integral of wear depth over the contact surface, was similar to the value calculated using Archard’s law.
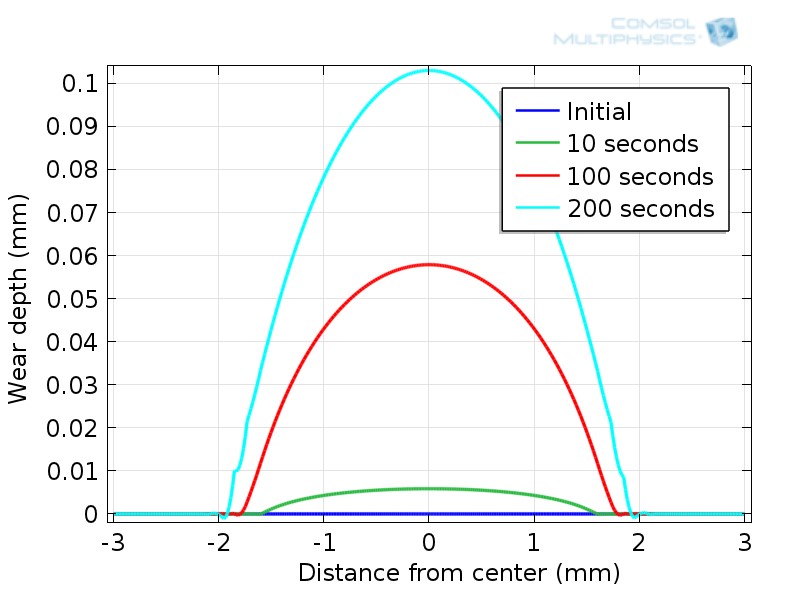
Wear depth vs. radial distance in the pin-on-disc model.
Predicting Wear
We also used the model to predict wear in an automotive disc brake problem, which is similar to the Heat Generation in a Disc Brake model that can be downloaded from the COMSOL Model Gallery. We developed a 3D thermal-structural disc brake model involving representative brake disc/rotor and brake pads.
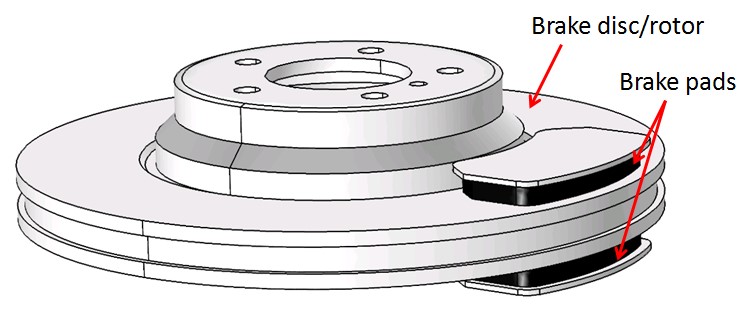
Disc brake model used in the COMSOL Multiphysics wear simulation.
The structural and thermal processes are coupled through frictional heat generation, thermal expansion, and thermal contact. Both physics fields are also coupled to the wear depth evolution boundary ODE. We used a fully-coupled direct solver that converged rapidly, keeping solution times similar for problems with and without wear.
The results for both the pin-on-disc validation example and the disc brake problem were in good agreement with published wear data. In the disc brake example, the model captured the non-uniform wear rate that is typically observed on brake pads; it was higher near the outer radius and leading edge, as shown below.
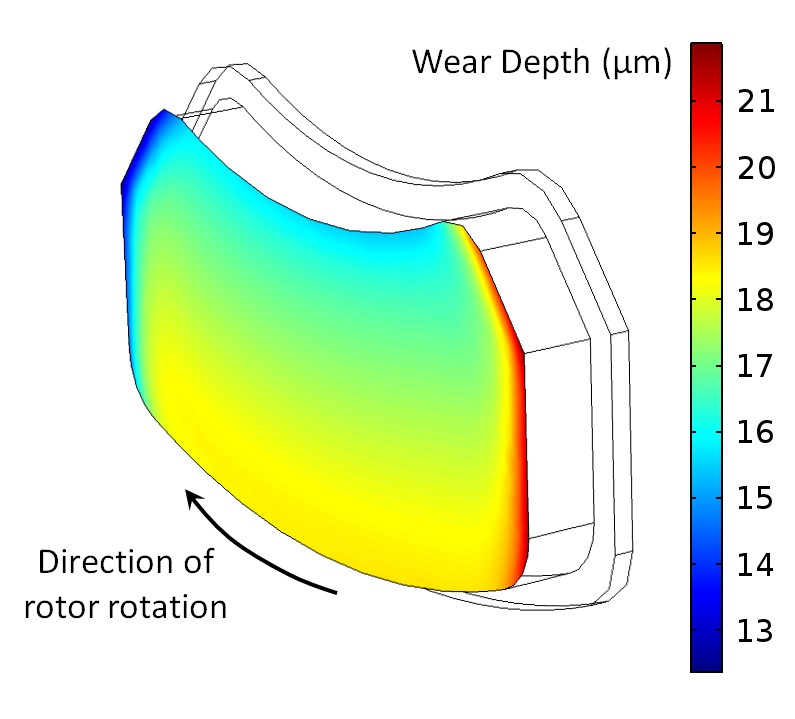
Typical brake pad wear depth profile.
We will present more of our results, including contact pressure and wear contours, at both the Cambridge and Boston stops of the COMSOL Conference 2014.
About the Guest Author
Nagi Elabbasi, PhD, is a Managing Engineer at Veryst Engineering LLC. Nagi’s primary area of expertise is modeling and simulation of multiphysics systems. He has extensive experience in finite element modeling of structural, CFD, heat transfer, and coupled systems, including fluid-structure interaction, conjugate heat transfer, and structural-acoustic coupling. Veryst Engineering provides services in product development, material testing and modeling, and failure analysis, and is a member of the COMSOL Certified Consultant program.




Comments (15)
Daniel Sutton
November 13, 2014A very interesting article, and something I am keen in implement myself. I have previously implemented Archard’s wear law in COMSOL using LiveLink for MATLAB (http://www.uk.comsol.com/paper/simulation-of-wear-using-livelink-for-matlab-16581), but your method allows for a time-dependent analysis analysis of wear which would be very useful for e.g. viscoelastic materials, unlike my current approach.
Unfortunately I am having issues engaging the contact pair when a boundary ODE is defined in the contact gap. I wonder if you had any issues when solving, and what solver / specialized solver or contact pair settings you used when solving the problem?
Thanks,
Dan
Nagi Elabbasi
November 14, 2014Hi Dan, thanks for point out your interesting article. Did you use the wear depth to move the surface nodes, or did you adjust the contact gap like we did? The two important settings that helped us reach convergence for this problem were (i) penalty contact, and (ii) first order BDF time stepping.
Daniel Sutton
November 17, 2014Thank you for your quick response. To answer your question, in my previous work I relocated the surface nodes according to wear depth. I developed a script in MATLAB to control the process, which solves in a very reasonable time-frame.
I will try as you suggest – thank you for you help!
Dan
khaled harmouch
September 9, 2016Hello Nagi
Wear simulation is something that I have been doing short while ago. However, I have noticed that finding the wear coefficient and the hardness values for a pair of materials in contact is not an easy thing to do. If you have recommendation for materials property reference, what it will be?
And I have another question concerning the modeling, I have tried to simulate the vibrational behavior of two objects in contact in time dependent model and I had divergence issues (I use a penalty contact and a first order BDF time stepping), do you have an idea where the problem might be?
Thank you in advance
Khaled
Nagi Elabbasi
September 9, 2016Hi Khaled,
Yes, it is hard to find wear coefficients. An online search will get you typical values for common material combinations, especially in the dry condition. Hardness values are easier to find online. Direct testing to evaluate the wear rate is best of course, and is not that complex (usually using a variant of the pin-on-disc example shown above).
Vibration problems are harder to converge compared to this example because the friction state and friction force direction will be changing with time, but they are still solvable. Hard to tell what’s causing the convergence difficulty in your model without examining it. Here are three tips that generally help: (i) use smaller time steps to better capture the vibration, (ii) add damping, and (iii) use the Automatic Newton or the Automatic Highly Nonlinear Newton settings in the solver.
khaled harmouch
September 12, 2016Hi Nagi,
Thank your for your answer, apparently the third tip was the solution for convergence. The simulation time is though relatively long.
Speaking about material properties like wear coefficient, I am afraid that I wasn’t clear in my comment above! The problem isn’t really in finding the material coefficient, the issue is in the diversity of answers to that!! I found several material data sheets in which every data sheet gives a different wear coefficient, for example, then the other. I am wondering if you recommend a specific reference of material properties on which your studies are based.
Thanks
Khaled
Krishnamurti Singh
December 2, 2017I am new on Comsol and I want to know how to start with for dry sliding wear simulation
eslam mahmoud
December 2, 2018HI Nagi,
your work is really interesting, after reading your presentation i started to build wear model for predicting wear as i am studing tribology and care about wear behaviour of material.
my question for you you used archard’s wear equation and you said that K WEAR coefficient is function of (T ,H) how can i produce equation that will show the variation of wear coefficient with
temperature and hardness as hardness is measured before starting the experiment,
also as you know by changing speed and pressure the wear coeff will also change ,when experiment is finished i used to measure weight of specimens to detect weight losses and evaluate wear coefficient so how can i produce equation to relate it with volume loss in the model to predict wear in all cases thank you.
Nagi Elabbasi
December 2, 2018Thanks Eslam. I would start simple and assume the wear coefficient to be a constant or a linear function of temperature. Then find the wear constants that give the best fit of simulation to test data. For test data consider measuring local wear variation if you can, instead of just total weight loss. That gives you more data to calibrate your wear model. Having temperature measurements also helps with model validation, since it is hard to accurately predict temperature rise for such problems solely based on simulation data (assuming that the parts heat up during wear testing). If the fit to all test data is good enough, then you have a good wear model!
eslam mahmoud
December 11, 2018eslam mahmoud
December 11, 2018thank you nagi very much,
i am really facing many problems and need your help, first i am trying to build only wear model without heat effect as you told me now we select boundary ode i tried to solve it in two dimensions i build geometry for pin and disk now i should select the contact face as the boundary for solving the ode . in your work when you selected the boundary ode there was inside this physics (distributed ode1-initial values and you finally select distributed ode2)
i didnot understand that because in first distributed ode 1 the boundary select all and cannot be changed while selecting distributed ode2 i can select boundary for contact faces.
i need your help if you can send me how to solve this ode in 1d 2d 3d geometry and what is necessary to select thank you very much
Salvatore Siani
March 1, 2021I’m simulating a Pin-On-Disc wear test and I found this article very interesting. I would like to know if it’s possible, what kind of boundary conditions did you apply to your model?
Nagi Elabbasi
March 1, 2021Dear Salvatore,
I believe I fixed the bottom of the disc, and just applied the sliding velocity (resulting from the movement of the disc) to the contact interface, just like I applied the wear equations. All this is now doable without additional equations as features in the new COMSOL wear implementation in version 5.6.
Regards,
Nagi
保华 文
April 11, 2022Dear Nagi Elabbasi
I’m a graduate student doing a wear simulation and this article of yours has been very helpful to me. I’m also doing pin and flat wear. However, I have encountered some problems, which cannot be ruled out. I have tried many methods and still cannot solve them. So here, I hope you can give me some help, it is best to share this case as a learning material to help students in developing countries gain better knowledge.
Thank you so much for sharing, I really appreciate your reply.
保华 文
April 11, 2022Dear Nagi Elabbasi
I’m a graduate student doing wear simulation and this article of yours has been very helpful to me. I’m also doing pin and fdisc wear. However, I have encountered some problems, which cannot be ruled out. I have tried many methods and still cannot solve them. So here, I hope you can give me some help, it is best to share this case as a learning material to help students in developing countries gain better knowledge.
Thank you so much for sharing, I really appreciate your reply.