The Application Gallery features COMSOL Multiphysics® tutorial and demo app files pertinent to the electrical, structural, acoustics, fluid, heat, and chemical disciplines. You can use these examples as a starting point for your own simulation work by downloading the tutorial model or demo app file and its accompanying instructions.
Search for tutorials and apps relevant to your area of expertise via the Quick Search feature. Note that many of the examples featured here can also be accessed via the Application Libraries that are built into the COMSOL Multiphysics® software and available from the File menu.
Shape Optimization of a Wrench
This model shows how to use the Free Shape Boundary feature to increase the stiffness of a wrench without increasing its mass. Read More
Bracket — Topology Optimization
This example shows how to perform a topology optimization with several load and constraint cases. The density feature for topology optimization is used together with a parametric sweep where each optimized solution is used as input for a further improved optimization. The final ... Read More
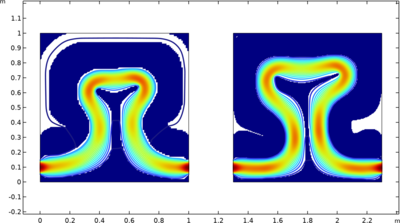
Topology Optimization of a Heat Exchanger with Laminar Flow
This model demonstrates topology optimization of a 2D heat exchanger with laminar flow. The flow is pressure driven and the objective is to maximize the heat transfer. The density method is used with the (now) classical approach of a single design variable and two flow interfaces. ... Read More
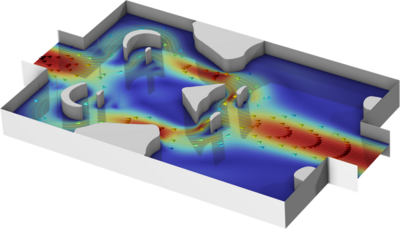
Optimization of a Tesla Microvalve
This model performs a topological optimization for a Tesla microvalve. A Tesla microvalve inhibits backwards flow using friction forces rather than moving parts. The design can be optimized by distributing a specific amount of material within the modeling domain. The goal is to maximize ... Read More
Metalens Design App
This is a simple yet powerful simulation app for designing a two-dimensional reflective metalens. This metalens consists of a array of glass nanopillars on a metal substrate. Initially, the app determines the optimal grating parameters for a specific wavelength and calculates the ... Read More
Topology Optimization of a Magnetic Circuit
This model presents two examples of topology optimization of the magnetic circuit of a loudspeaker driver. A first optimization is used to find the design of a nonlinear iron pole piece and top plate that maximize the BL factor at the resting position (small displacements), while ... Read More
Topology Optimization of an MBB Beam
A demonstration of topology optimization using the Structural Mechanics Module and the Optimization Module. The classical MBB beam is solved in 2D using a Helmholtz filter and Solid Isotropic Material Penalization (SIMP) technique to recast the original combinatorial optimization problem ... Read More
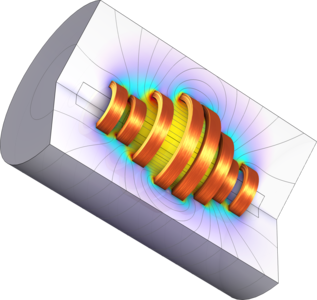
Shape Optimization of Coils
This example shows how to use the Optimization Module to find a coil geometry giving a uniform magnetic field on axis and minimal field near the axis ends. Read More
Mooney–Rivlin Curve Fit
This presentation shows how to use the Optimization Module to fit a material model curve to experimental data. It is based on the hyperelastic Mooney-Rivlin material model example given in the Structural Mechanics users guide. Read More
Parameter Estimation for a Tensile Test
The model shows how to estimate the Young's modulus and Poisson ratio based on a tensile test. The test measures the tensile force and the radial displacement for different values of the prescribed displacement. The model is based on synthetic data generated in the model itself. It is ... Read More