
Suppose you have a very long system with a constant cross section: a fluid-filled pipe. Modeling this system is computationally expensive and time consuming. Using a guided wave propagation approach, you can model a cross section of the system and compute the guided waves along it. You can represent such waves by means of dispersion curves. Here, we discuss a coupled analysis considering air and water as the internal fluids. We also analyze the system dynamics using dispersion curves.
Fluid-Filled Pipes: A Modeling Challenge
Fluid-filled pipes, also referred to as fluid-carrying structures, have a large number of industrial applications, such as gas pipelines, automotive mufflers, aircraft fuselage, and underwater pipelines. The size of a pipeline system can range from centimeters to kilometers.



Common applications of fluid-filled pipes. Left: A submerged pipeline. Image by Grand Canyon National Park. Licensed under CC BY 2.0, via Flickr Creative Commons. Center: A model of an aircraft fuselage. Right: An automotive muffler. Image by lw5315us. Licensed under CC BY-SA 2.0, via Flickr Creative Commons.
Large pipe systems are difficult to model with simulation software, and because acoustic and elastic modes don’t exist independently, individual analysis doesn’t make it easier. Therefore, we need to underline the effect of fluid loading on the response of the pipe.
At low frequencies, the fluid loading term tends to be small, so the response of the system is dominated by the dynamics of the structure/pipe (Ref. 2). Fluid loading changes the vibrational characteristics of the structure in contact, and consequently, the acoustic radiation. Fluid-loading effects are exhibited strongest by structures in contact with denser fluids, since the fluid forces are proportional to the mean density of the fluid.
What Are Dispersion Curves?
Generally, systems can be described by distributed mass and stiffness. There are infinite degrees of freedom (DOFs) for a continuous system, which results in infinite modes. For a finite frequency range, there is a finite number of modes that can be analyzed individually using modal decomposition. The motion of such continuous systems is described by partial differential equations (PDEs) from force/acceleration and force/deformation relations. Examples of such systems are strings, rods, and shafts (second-order PDEs) as well as beams (fourth-order PDEs) and fluid-filled pipes.
The solution to such equations can be visualized using two approaches:
- Eigenmodes
- Wave representation (or wave modes)
Suppose we’re interested in modeling the dynamics of a large system at higher frequencies using the finite element method (FEM). To capture its behavior, the wavelength must be discretized with a sufficient number of elements, which could result in a large number of DOFs and more memory and time. We can tackle this issue using wave modes or representing the system as guided waves, since the waves travel long distances before they decay.
Wave properties are another advantage of a wave-based approach. They are important for studying structure-borne sound, frequency response of finite-length waveguides, and computing the energy transmission through structures. You represent these wave modes through dispersion curves, which provide a relationship between the wave number and frequency.
Dispersion curves are basically separate lines that each represent an individual mode. The only prerequisite for the wave-based method is that the cross section of the system is constant (there is no limit to the length). For modeling long systems, such as pipes carrying fluid, beams, or rail track, the wave-based approach is very useful.
Using Dispersion Curves to Analyze Fluid-Filled Pipes
Waves propagate in time and space. The spatial variation is described by a quantity representing phase change per unit distance and is equal to ω/c. This is the wave number, denoted by k. One wavelength corresponds to an x-dependent phase difference of 2π: kλ = 2π.
When a system is excited with a force at one end, a large number of waves start to propagate to the other side. Each wave travels with a velocity described as the phase velocity (independent of ω; e.g., longitudinal shear waves) and group velocity (frequency dependent; e.g., bending waves). All of the waves travel together under an envelope. The speed at which the energy is transported is given by the group velocity, which is the velocity of the envelope given by cg = ∂ω/∂k.
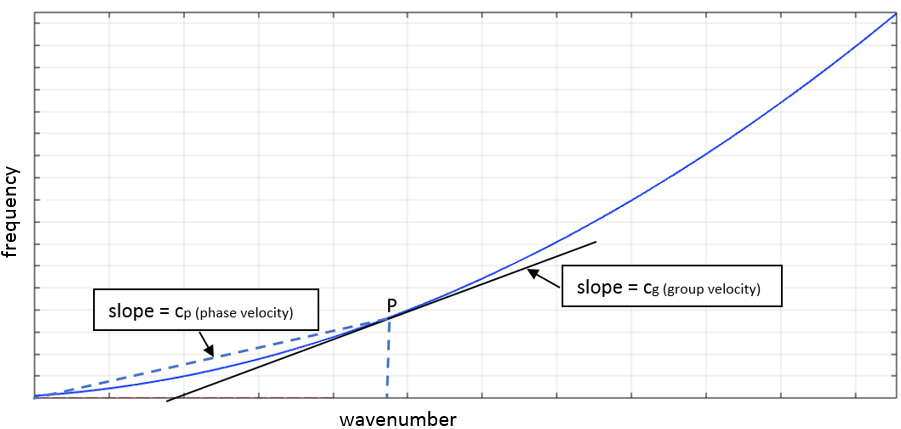
Schematic of a dispersion curve.
Dispersion curves explain the dynamics of a coupled system. In a fluid-filled pipe where waves can travel in fluid as well as in the pipe wall, the dispersion curves provide a common wave number or wave mode that propagates into the system as a whole. Dispersion curves also provide insight into what happens inside the system at different frequencies. Let’s see how to compute dispersion curves analytically.
Wave Modes of a Hollow Pipe and a Rigid-Walled Acoustic Pipe
Consider a linear conservative system that is uniform and unbounded in one direction (z). The equation of free vibration can be written as:
(1)
where μ(z) is the mass density, and L(z) is the stiffness operator and depends on z,\; \frac{\partial}{\partial z},\; \frac{\partial^2}{\partial z^2},… and so on.
The exact form varies. In general, w might be a function of 1, 2, or 3 space variables depending on the problem (such as a beam, plate, or acoustic cavity). Under the passage of a time-harmonic wave, the solution of Eq. (1) is w(z,t) = Wei(ωt – kz), where W is the amplitude of the wave, ω is the circular frequency, and k is the wave number.
Substituting w(z,t) in Eq. (1) provides the dispersion/characteristic equation. The solution is wave numbers, which come in pairs and represent waves traveling in the ±z direction. Wave numbers can be characterized as:
- Propagating (purely real values of k)
- Evanescent (purely imaginary k)
- Attenuating oscillating (complex value of k)
Structural Modes
We may want to obtain basic wave modes (such as longitudinal, shear, and bending) of a structure analytically. Systems considered here have a constant cross section and wave propagation in the positive x direction. For computing longitudinal motion, consider a uniform elastic bar with density ρ and Young’s modulus E. The equation of motion for free vibration is given by E\frac{\partial^2u}{\partial z^2}-\rho\frac{\partial^2u}{\partial t^2}=0. Using the same principle as for time-harmonic motion, we get the dispersion relation k=\omega\sqrt\frac{\rho}{E}, with phase velocity c_L=\frac{\omega}{k}=\sqrt\frac{E}{\rho} and group velocity cg = cL. Since cL is independent of ω and k, all harmonic waves travel at the same speed. The dispersion relation for shear waves is of the form k_s=\omega \sqrt\frac{\rho}{G}, where G is the shear modulus of the material.
To compute the bending waves, we consider the Euler-Bernoulli and Timoshenko theories based on certain assumptions. The Euler-Bernoulli theory assumes that the cross section of the beam remains plane and perpendicular to the neutral axis during bending, ignoring rotary inertia and shearing effects. This simplifies many terms and yields a fourth-order partial differential equation, EI \frac{\partial^4w}{\partial z^4}+\rho A \frac{\partial^2 w}{\partial t^2}=0, which can be easily solved.
The only problem with this assumption is that it cannot be validated at high frequencies when the wavelength becomes comparable to the thickness of the structure. The dispersion relation is given by k_b=\bigg(\frac{\rho A}{EI}\bigg)^{1/4}\sqrt\omega, corresponding to phase velocity c_b=\bigg(\frac{EI}{\rho A}\bigg)^{1/4}\sqrt\omega and group velocity cgb = 2cb. The phase speed depends on frequency, so the bending waves are dispersive. The wave spreads out due to higher-frequency components, which propagate faster.
Other theories, such as Timoshenko, incorporate shear effects and provide more accurate behavior at higher frequencies. For complicated cross sections, analytical solutions are not feasible.
Acoustic Modes
The acoustic pressure field inside a cylindrical duct, which satisfies the acoustic wave equation, is given by:
where n is the circumferential mode order, Pn is the amplitude coefficient, Jn(krr) is the Bessel function of first kind, kz is the out-of-plane wave number, and θ is the circumferential angle.
The radial wave number kr is determined by the boundary condition for a rigid wall; i.e., Jn‘(krr)r=a = 0 , where Jn‘(krr) is the derivative of the Bessel function with respect to r. The solution/modes are multivalued for a given n. Correspondingly, the out-of-plane wave number is computed using the relation kz2 + kr2 = k2.
Using the Mode Analysis Solver in COMSOL Multiphysics®
Our fluid-filled pipe is linearly elastic and homogeneous. The fluid is purely acoustic, which means it’s compressible, inviscid, and barotropic. The pipe’s modes are computed individually. For the numerical example, the pipe material is steel and the fluid is air. Material properties are given by:
| Material Properties |
|---|
| E = 2e11 N/m2 |
| ρs = 7800 kg/m3 |
| ν = 0.3 |
| ρf = 1.25 kg/m3 |
| Speed of sound in air, c = 343 m/s |
| ro = 0.05 m |
| t = 0.0025 m |
We use the Solid Mechanics interface and Pressure Acoustics, Frequency Domain interface to solve the model. We also use the mode analysis study type, where the modes or out-of-plane wave numbers are computed at each frequency. Mode analysis assumes that the mode is harmonic in space; i.e., u(x,y,z) = u(x,y)eikzz. This equation can be solved at a given frequency for free vibrations for most of the out-of-plane wave numbers, kz.
Certain discrete values — eigenvalues — correspond to the wave numbers of the propagating or evanescent modes. The mode analysis study step triggers the solver that can find these wave numbers and the corresponding mode shapes. A parametric sweep of frequency computes the wave numbers at different frequencies.
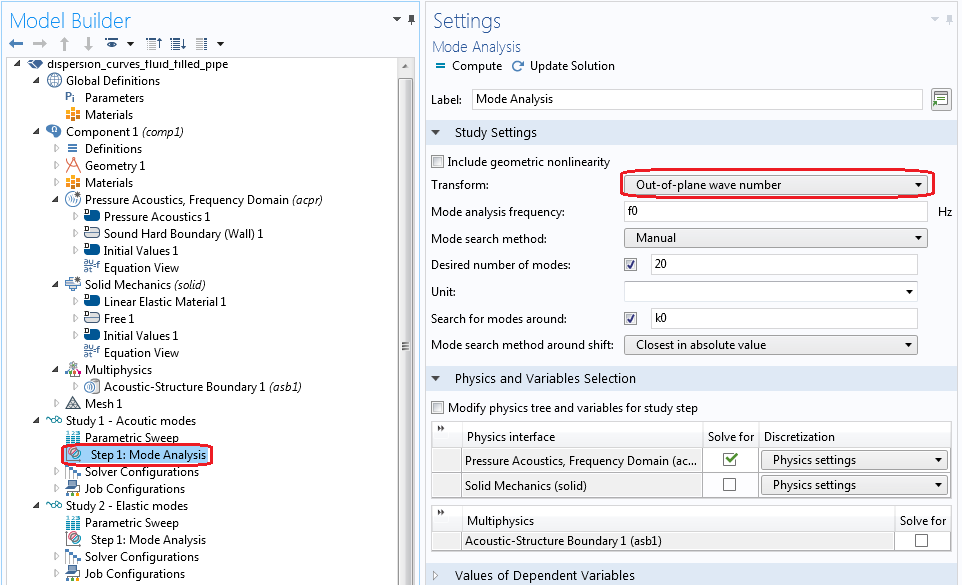
Settings for computing out-of-plane wave numbers.
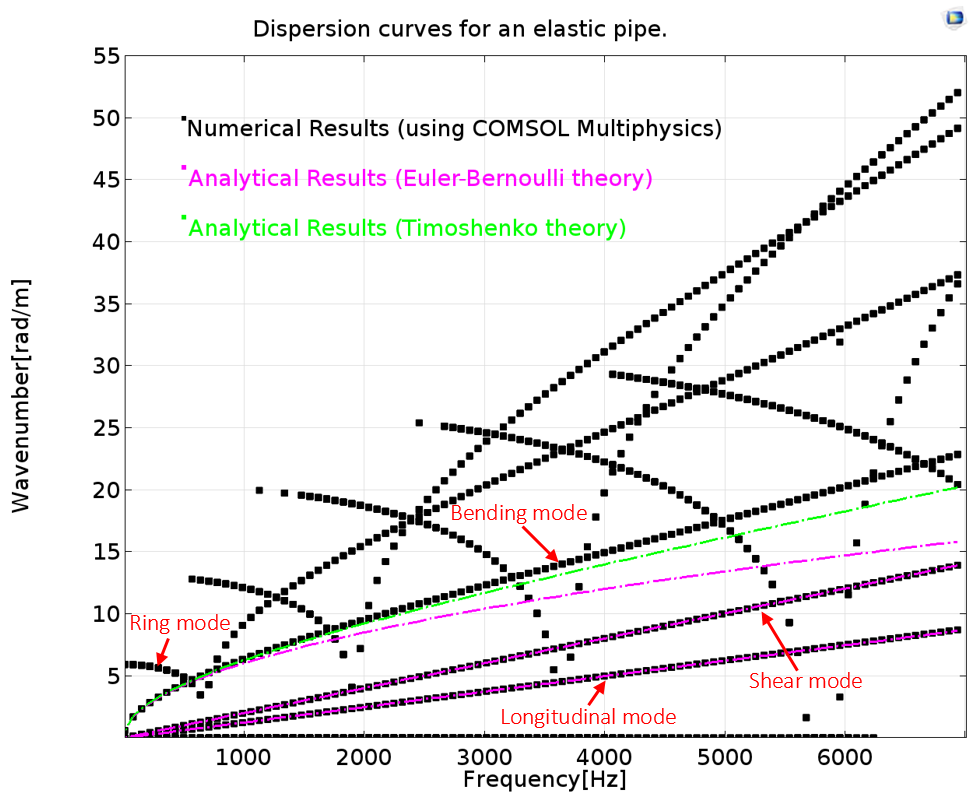
The real values of the wave numbers are plotted, since they correspond to propagating wave modes. The cross-sectional shapes are also plotted in terms of total displacement. To read the dispersion curve, we use the lines (see below). Comparing the bending, shear, and longitudinal modes with analytical solutions helps to easily identify them. We also see a mode cuts on at around 6000 Hz and propagate from there. Sometimes, the behavior of the mode changes at high frequencies (a bending mode can convert into a shear, longitudinal, or extensional mode). Such behavior can be easily captured with dispersion curves.
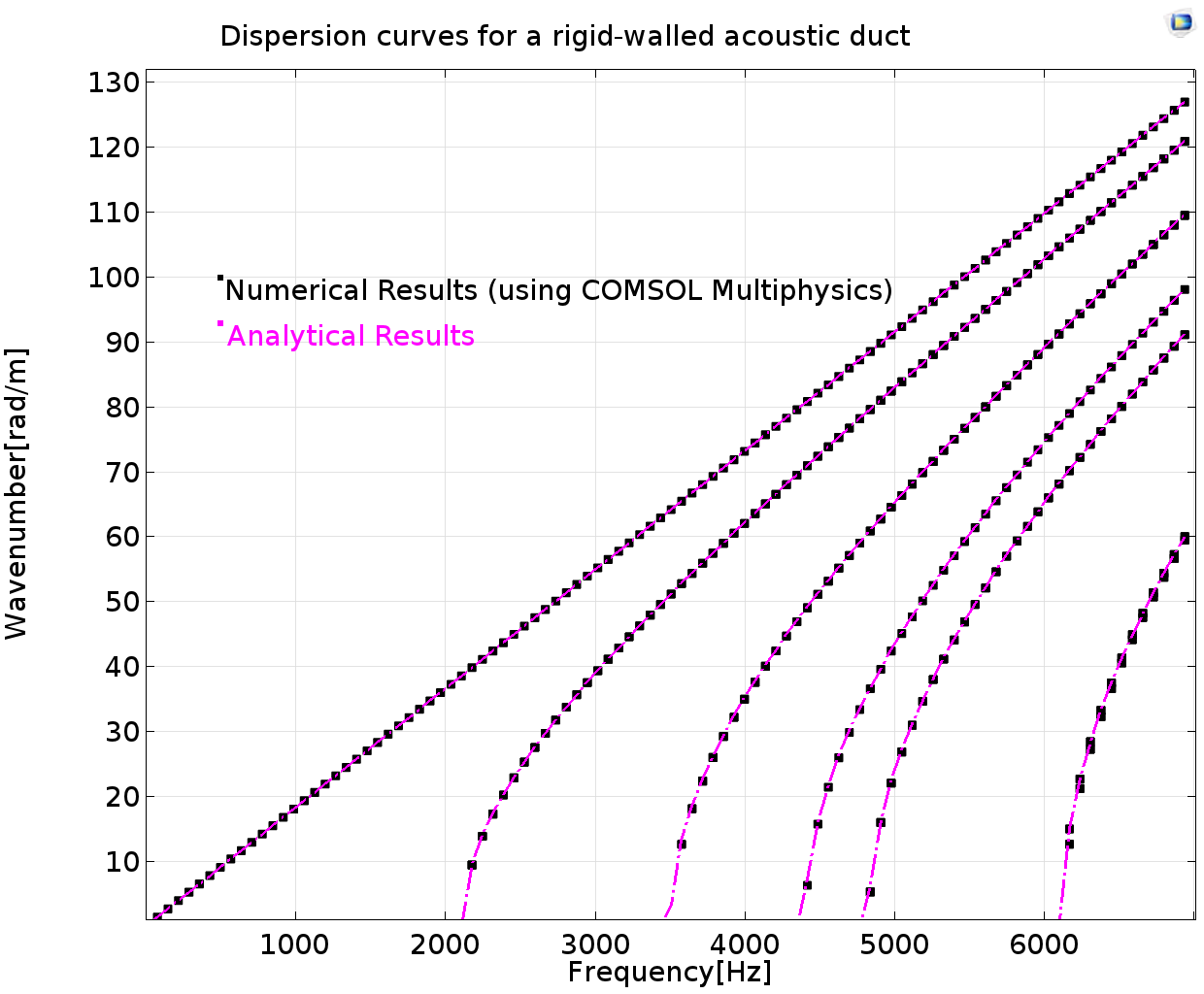
Dispersion curves for a hollow cylindrical pipe (left) and rigid-walled acoustic duct (right).
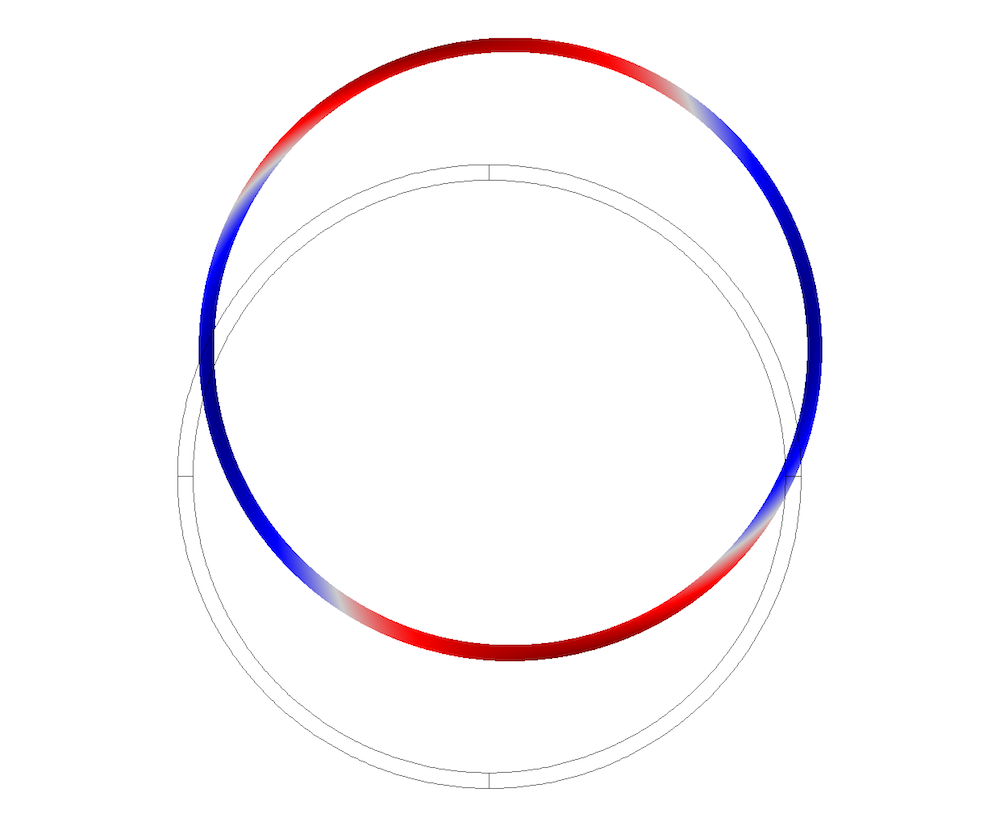
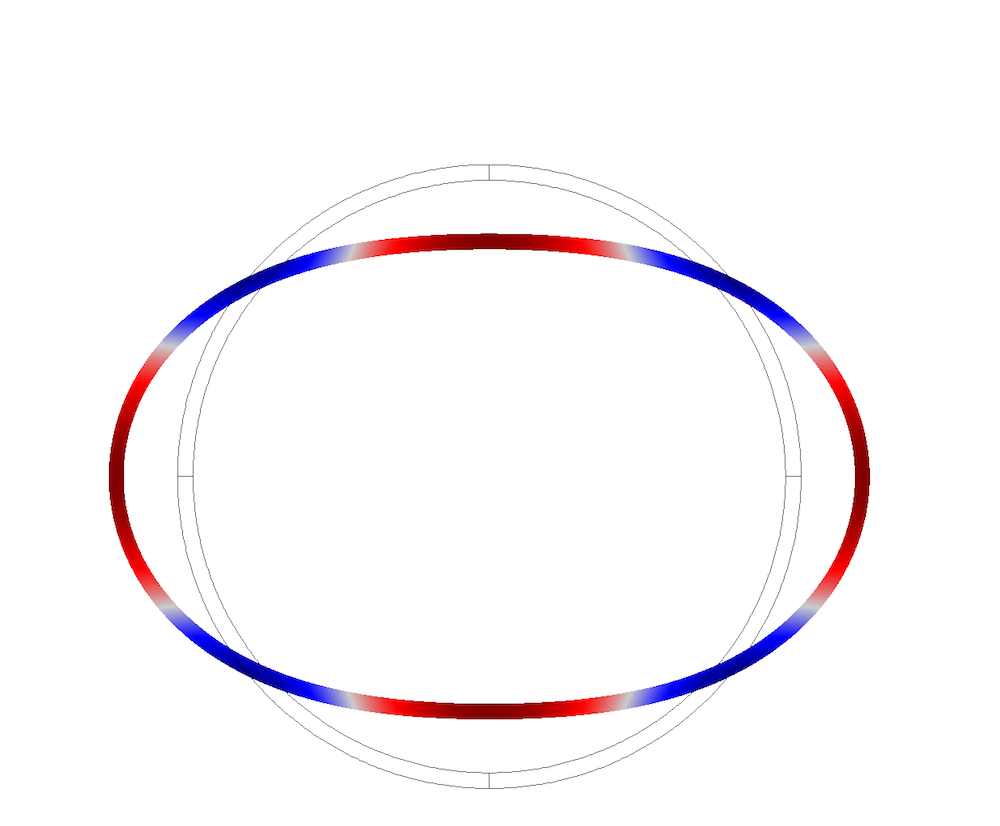
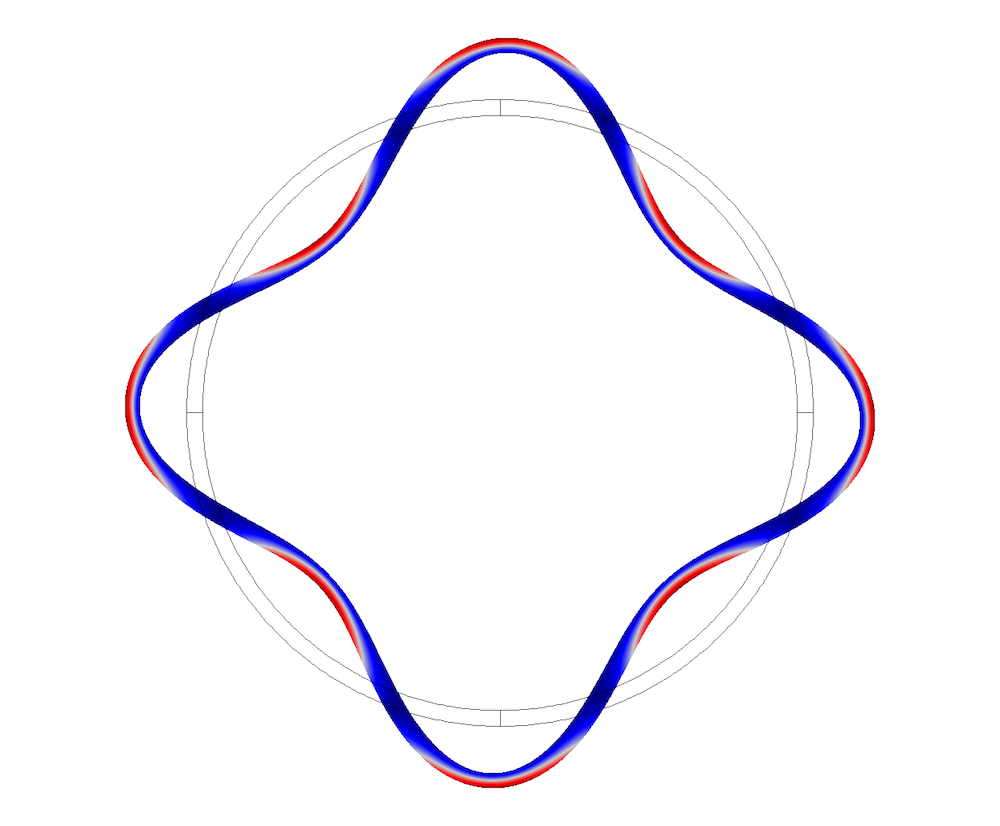
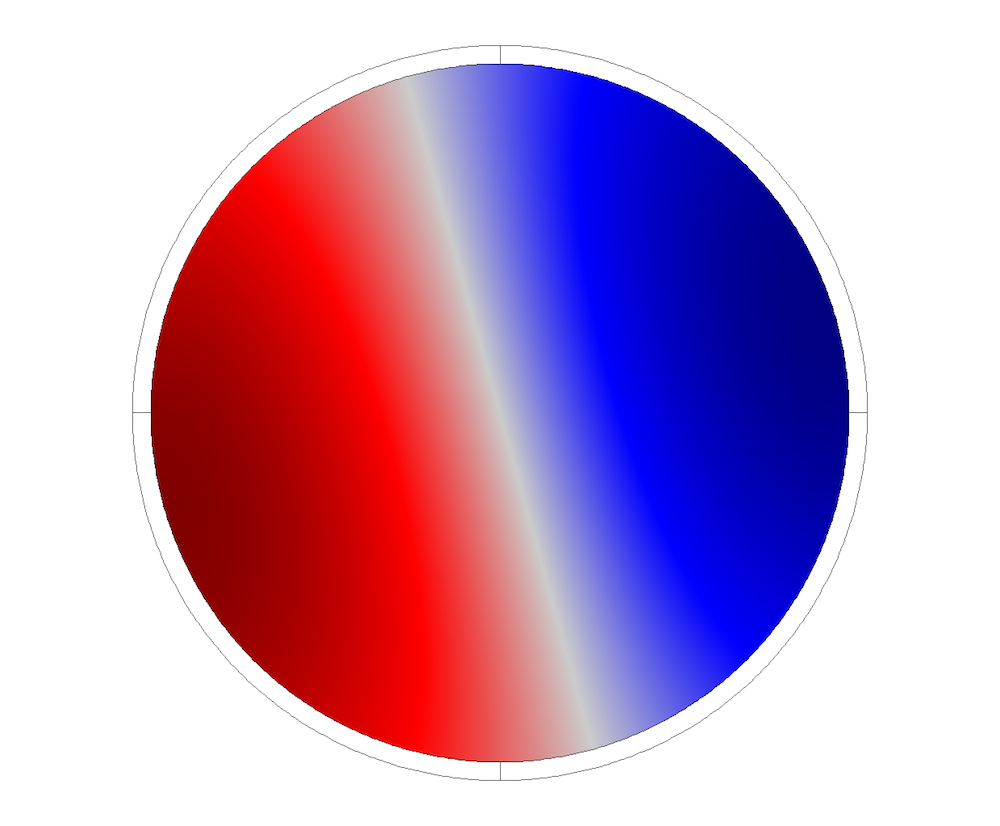
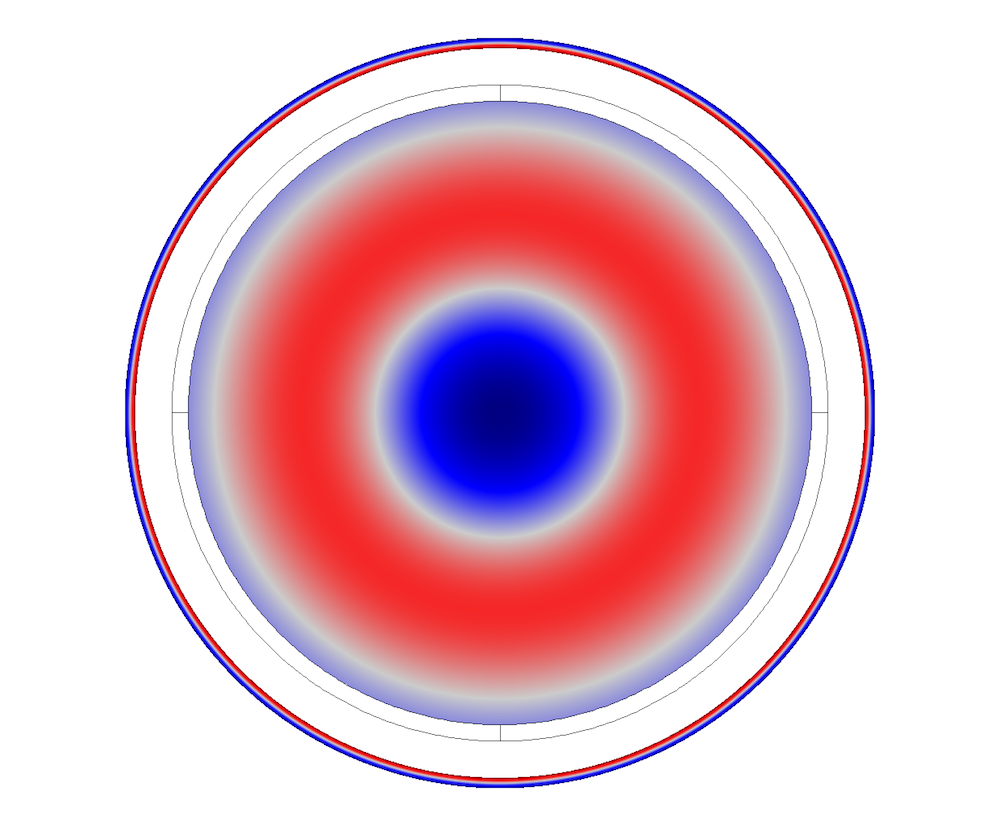
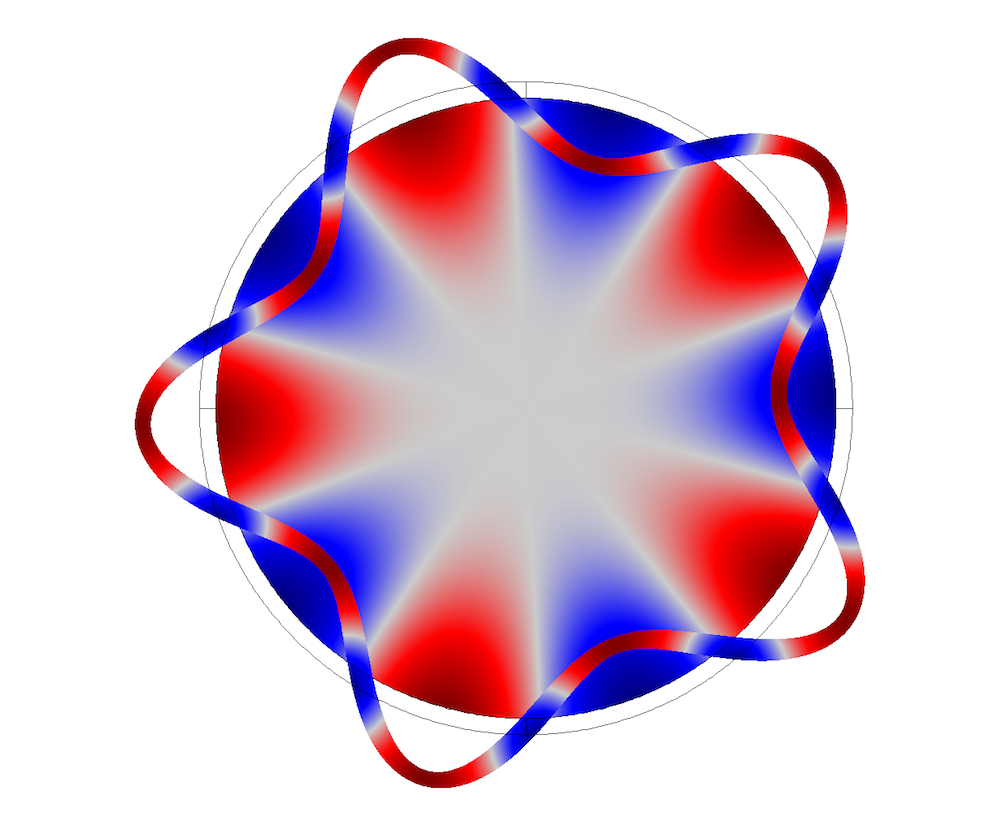
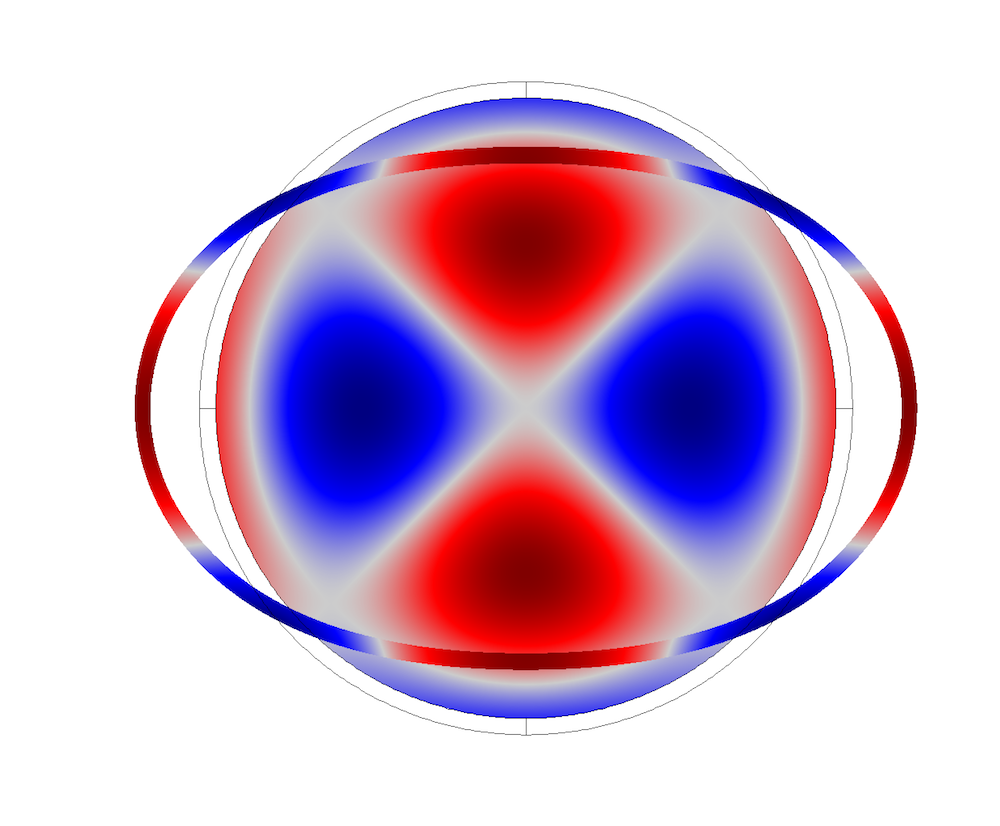
Pipe cross-sectional mode shapes.
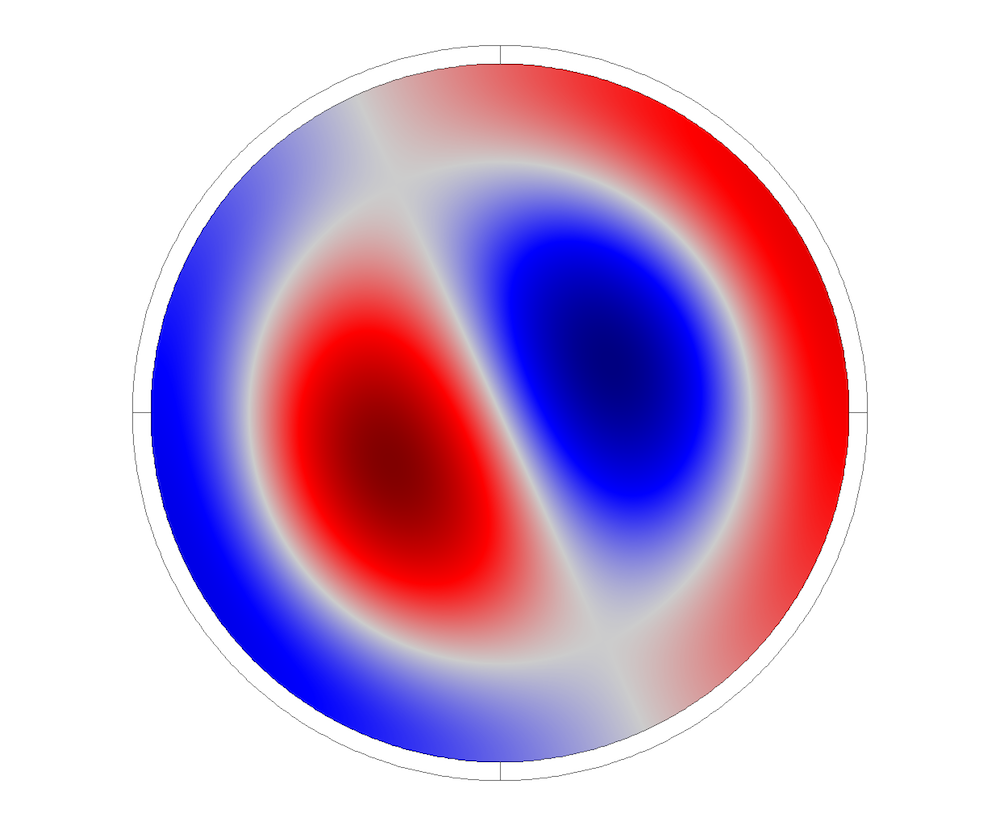
The dispersion curves for a cylindrical rigid-walled pipe can be analyzed using the same analogy. The first 6 acoustic modes (see graph above to the right) cut on at around 2000, 3500, 4300, 4800, and 6100 Hz, respectively. The modes are compared with the analytical solutions and the cross-sectional shapes are plotted for the cylindrical duct, also showing the pressure distribution across the duct cross section.
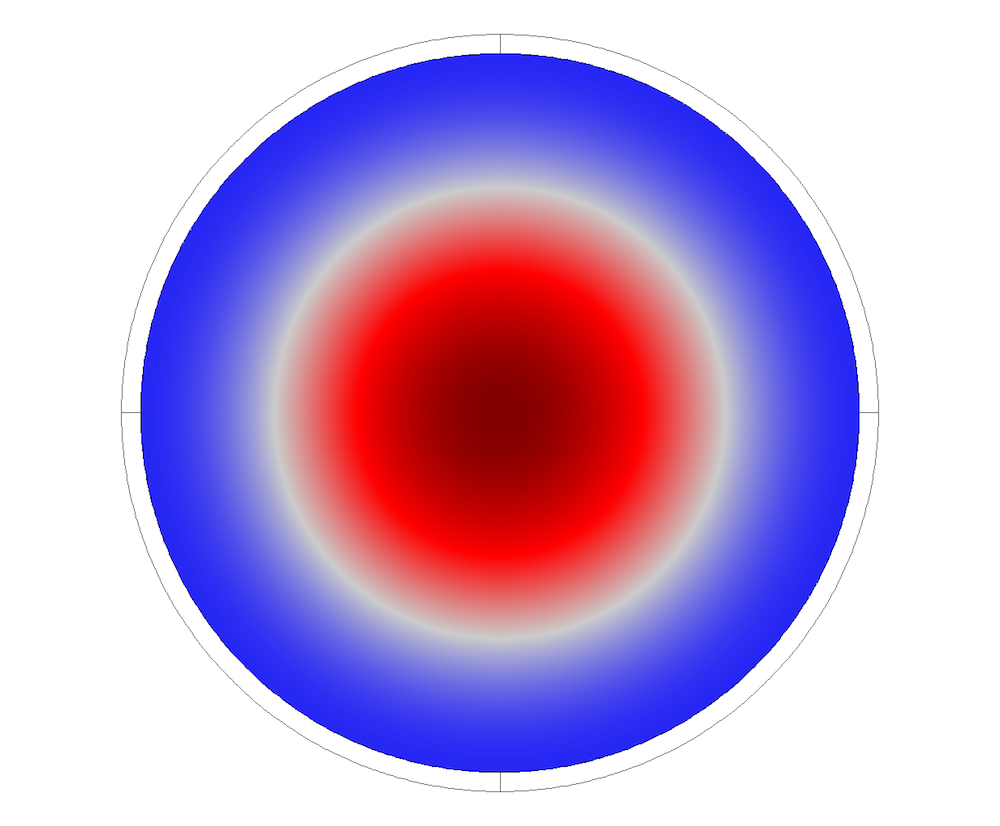
Pressure distribution at different modes.
The wave numbers computed using the COMSOL Multiphysics® software are compared with the analytical wave numbers of the hollow pipe and rigid-walled cylindrical duct, respectively. Results show good agreement, but there are clear differences observed for the bending mode. Since the analytical theory is based on assumptions, it cannot be used for high frequencies. The reliability of numerical results lies in the proper discretization of the domain under study.
Note that a sufficient number of elements per wavelength (~6–8 quadratic elements) must be used to capture the wavelength accurately. Another advantage of the numerical approach is that analytical solutions are difficult to obtain for complex cross sections (such as multilayered pipes or complex shape cross sections). In the plot above to the left, apart from the regular wave modes (i.e., bending, longitudinal, shear), many other modes are observed in the numerical solutions. This number increases with the frequency range. The “extra” modes (such as the ring mode) also have physical significance and they are extremely difficult to obtain via analytical solutions. The system’s overall dynamic response is the superposition of all of the modes.
At a higher frequency range, the system’s behavior becomes more complex. Modes overlap with each another and it’s extremely difficult to understand the behavior of each mode. Again, dispersion curves come to the rescue.
Computing the Wave Modes of a Fluid-Filled Pipe
Now, we compute the wave number for the coupled system for the fluid-filled pipe. Using the method described earlier, the wave modes are computed using the mode analysis solver in COMSOL Multiphysics for both air and water as the internal fluid.
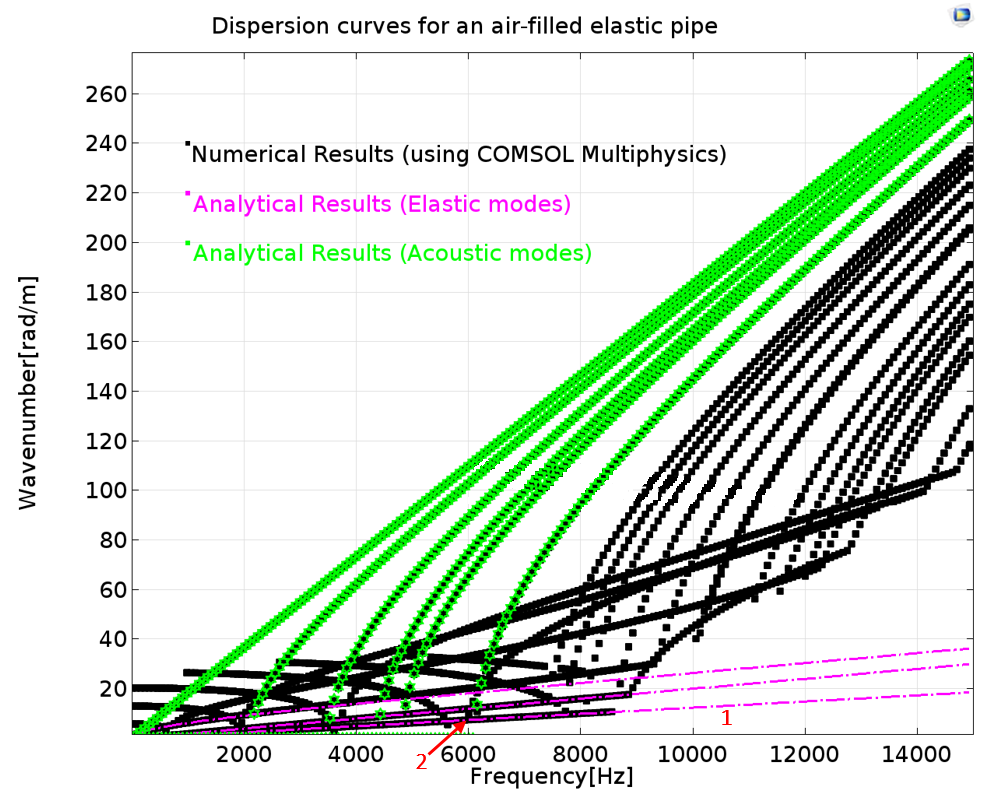
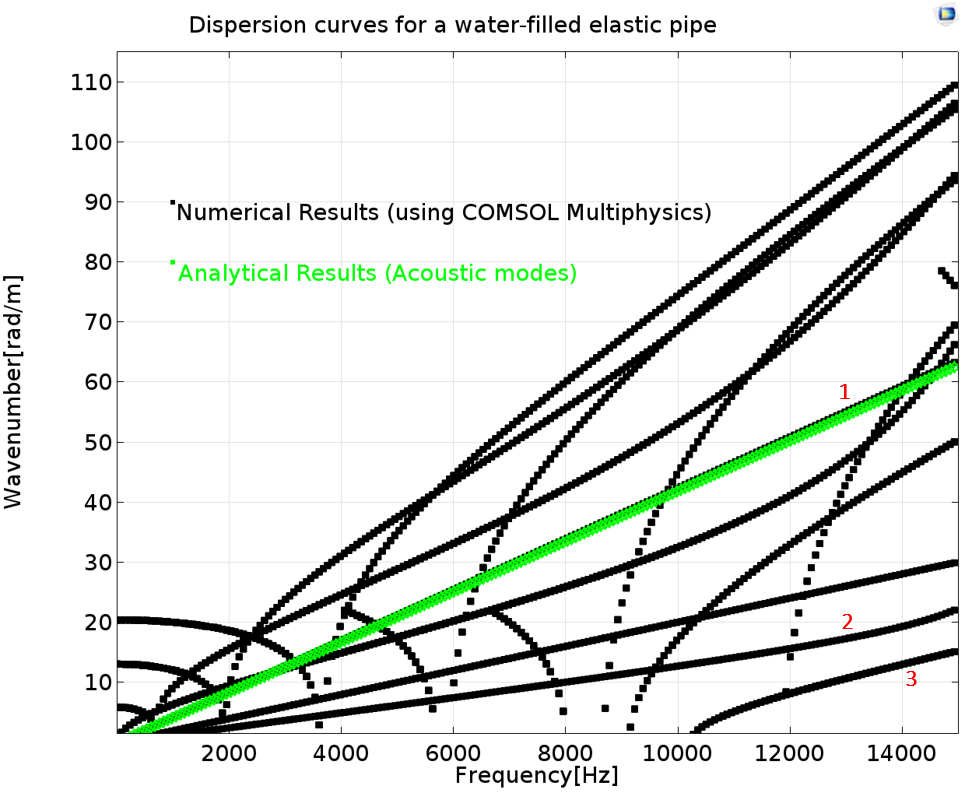
Dispersion curves for an air-filled (left) and water-filled (right) steel pipe.
The results for the air-filled steel pipe are compared with the uncoupled acoustic and elastic modes. Since the fluid is light, it has minimal effect on the vibrations of the coupled system.
The ring mode can be seen at low frequencies where the pipe resonates as a ring. However, due to Poisson’s effect, there is a slight coupling between the elastic and acoustic parts. As the frequency increases, the motions of the elastic and acoustic parts become strongly coupled, highlighted by a rapid increase in radial vibrations. For instance, branch 1 corresponds to the longitudinal mode and branch 2 corresponds to the coupled mode. Although the coupling between air and steel is weak, at 6000 Hz, the extensional mode converts into an acoustic mode.
Cross-sectional mode shapes for the coupled system are plotted below. They correspond to the displacements in the pipe and pressure field in the fluid domain.
Strong coupling behavior is seen in the plot above for a water-filled pipe. Branch 1 corresponds to the acoustic wave in a rigid-walled cylindrical duct (purely acoustic mode). Considering branch 2, the pipe behaves in vacuo at low frequencies. At high frequencies, the fluid and pipe motion become strongly coupled and the mode converts into a second acoustic mode. Branch 3 originates (cuts on) at around 10,000 Hz. The mode seems to follow the trend of an extensional structural mode and at high frequencies, it again converts into a rigid-walled acoustic mode. We can analyze other branches similarly.
Coupled elastoacoustic wave mode shapes, with air as the internal fluid.
Further, dynamic analysis of the system using dispersion curves can be done at high frequencies. For finite-length systems, these propagation constants or wave numbers can be used to compute the forced response for significant computational efficiency.
Suppose you want to reduce the noise radiation from your system. A few easy techniques can be employed, such as using a multilayered/sandwich pipe made of soft rubber material enclosed by two stiff skins or a complicated cross section (maybe elliptical). Such complex configurations can easily be tested using dispersion curves.
However, the analysis must have:
- Linear elastic system or anisotropy along the cross section but not along the length
- A constant cross section, applicable for long (infinite) waveguides
- Adequate finite element discretization, and the size of the elements should not be too small to avoid any ill-conditioning issues
Concluding Thoughts
In this blog post, we have discussed how dispersion curves are computed for an infinite-length multiphysics system and how they can be further analyzed for structural mechanics and pressure acoustics. The analysis is performed using the mode analysis solver. In an upcoming blog post, we will demonstrate how to use wave modes to compute the forced response of finite length waveguides.
References
- F. Fahy and P. Gardonio, Sound and Structural Vibration: Radiation, Transmission and Response, Elsevier Academic Press, 2007.
-
C.R. Fuller and F.J. Fahy, “Characteristics of wave propagation and energy distributions in cylindrical elastic shells filled with fluid,” Journal of Sound and Vibration, vol. 81, no. 501518, 1982.
- A. Bhuddi, M.L. Gobert, and J.M. Mencik, “On the acoustic radiation of axisymmetric fluid-filled pipes using the Wave Finite Element (WFE) method,” Journal of Computational Acoustics, vol. 23, no. 3, 2015.








Comments (9)
Hassan Khalil
May 23, 2018Hi,
You wrote that:
“Dispersion curves are basically separate lines that each represent an individual mode. The only prerequisite for the wave-based method is that the cross section of the system is constant (there is no limit to the length).”
Did this statement (the use of the Mode Analysis study require an ‘infinitly long’ waveguide with constant cross section) also appliable to an optical waveguide (RF/waveguide module)?
Because i need to get the dispersions curve of a optical waveguide where the dimensions are small and comparable to the wavelength.
thanks,
Hassan Khalil
Hassan Khalil
May 23, 2018(RF/wave optics module)*
Sorry
Hassan Khalil
Ajit Bhuddi
May 24, 2018Hi,
Yes approach is applicable for optical waveguides as well. Please refer to the following blog and example model which will guide to the detailed approach for computing the dispersion curves for optical waveguides.
https://www.comsol.com/blogs/how-to-model-optical-anisotropic-media-with-comsol-multiphysics/
https://www.comsol.com/model/optical-anisotropy-blog-models-57481
Best Regards
Ajit
ABDELAZIZ RHAZZALI
October 24, 2018Hi Ajit,
Thanks for sharing your simulation and providing insightful explanation.
I am new to Comsol and i am trying to look in to the effect of the wall thickness in fluid filled pipes. I am trying to model the source as a plane waves not touching the wall at the entrance of the tube. How one could achieve that.
Thanks
Brianne Costa
October 29, 2018Hello Abdelaziz,
Thanks for your comment.
For questions related to your modeling, please contact our Support team.
Online Support Center: https://www.comsol.com/support
Email: support@comsol.com
James Lee
February 3, 2020Hi there,
Would you be able to make this file available for download?
Thanks
Ajit Bhuddi
February 3, 2020The model file link is already there at the end of the blog. You can download the file from there. Thanks.
James Lee
February 4, 2020There’s a link to the pdf/ppt but no file link for the simulation?
乾 周
April 16, 2020Hi,
I have downloaded the model file from the link. But the dispersion curves for the water-filled steel pipe in model was different from that in this blog. There was not branch 1 which corresponds to the acoustic wave in a rigid-walled cylindrical duct (purely acoustic mode), and many other details were also different. I have consulted Chinese engineers for this question. They told me to take the model result as the correct one. But I want to get the same result as that in this blog. Hope you can check the model file again. Looking forward to your reply.
Thanks!