The Application Gallery features COMSOL Multiphysics® tutorial and demo app files pertinent to the electrical, structural, acoustics, fluid, heat, and chemical disciplines. You can use these examples as a starting point for your own simulation work by downloading the tutorial model or demo app file and its accompanying instructions.
Search for tutorials and apps relevant to your area of expertise via the Quick Search feature. Note that many of the examples featured here can also be accessed via the Application Libraries that are built into the COMSOL Multiphysics® software and available from the File menu.
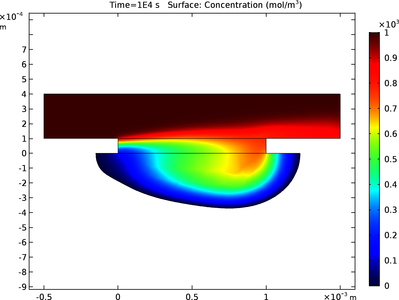
This example illustrates the principle of wet chemical etching for 2D geometry under laminar flow. The purpose of this tutorial is to examine how the copper substrate material is depleted and how the cavity shape evolves during the wet etching process. Wet chemical etching is ... Read More
A potential flow model of fluid flow in a rock fracture uses the so-called Reynolds equation. It shows how to use experimental data interpolated to a function used in the equation. Read More
The first stop for polluted water entering a water work is normally a large tank, where large particles are left to settle. Generally, gravity settling is an economical method of separating particles. If the fluid in the tank is moving at a controlled low velocity, the particles can be ... Read More
This is a tutorial model that demonstrates how to use mesh parameters such as Minimum element size Resolution of curvature Resolution of narrow regions Maximum element growth rate The instructions also detail how to access the mesh statistics and how to create a mesh plot. Read More
This is a benchmark model for an axisymmetric transient thermal analysis. The temperature on the boundaries changes from 0 degrees C to 1000 degrees C at the start of the simulation. The temperature at 190 s from the anlysis is compared with a NAFEMS benchmark solution. Read More
The stresses in a pulley connected to an engine that drives another pulley are studied in this model. A parametric analysis is conducted in order to study how the rotational speed affects the stress distribution in the pulley. The power at the pulley shaft remains constant, the moment ... Read More
This model shows how to perform a submodeling analysis in order to evaluate structural stress. Using a submodel helps to compute the results in a refined geometry detail while applying loads and constraints in the global model. Read More
Modeling the electrical activity in cardiac tissue is an important step in understanding the patterns of contractions and dilations in the heart. The heart produces rhythmic electrical pulses, which trigger the mechanical contractions of the muscle. A number of heart conditions involve ... Read More
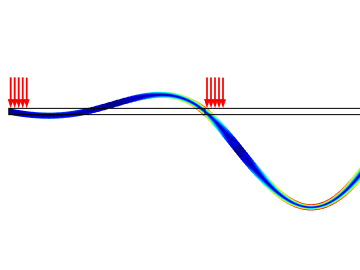
This example shows how to model a load which varies in space and time. A series of load pulses travel along a beam which is supported at equal distances. For some combinations of the traveling speed of the load pulses and the spacing between them, it is possible to excite resonances in ... Read More
This model simulates the pressure wave propagation in a muffler for a combustion engine. It uses a general approach for analysis of damping of the propagation of harmonic pressure waves. The model is solved in the frequency domain and provides efficient damping in a frequency range of ... Read More