The Application Gallery features COMSOL Multiphysics® tutorial and demo app files pertinent to the electrical, structural, acoustics, fluid, heat, and chemical disciplines. You can use these examples as a starting point for your own simulation work by downloading the tutorial model or demo app file and its accompanying instructions.
Search for tutorials and apps relevant to your area of expertise via the Quick Search feature. Note that many of the examples featured here can also be accessed via the Application Libraries that are built into the COMSOL Multiphysics® software and available from the File menu.
In this example of a peristaltic pump, rollers squeeze a flexible tube and the compression drives a fluid through the tube. The model demonstrates how to use the Fluid-Structure Interaction interface. The main advantage of the peristaltic pump is that no seals, valves or other internal ... Read More
This example presents transient analysis of the wave propagation in rock mass caused by a short duration load on the surface. Such loads are typical during tunnel constructions and other excavations using blasting. The example shows the use of the Low-reflecting boundary conditions to ... Read More
This model analyzes the frequency response of a fuel tank partially filled with fluid. The tank is submitted to a vertical acceleration. Two modeling methods are considered to represent the fluid: a traditional method of smearing the mass of the fluid through the wetted surface of the ... Read More
The drive for miniaturizing electronic devices has resulted in today’s extensive use of surface-mount electronic components. An important aspect in electronics design and the choice of materials is a product’s durability and lifetime. For surface-mount resistors and other components ... Read More
This tutorial example shows how to perform a random vibration analysis of a structure using power spectral density (PSD). The computations are based on the modal reduced order model (ROM). Read More
This example shows how to model prestressed bolts. The bolt geometry is taken from the Part Libraries. For comparison, one of the bolts is modeled using a thread contact formulation, whereas the other bolt is connected to the bolt hole by a pure continuity condition. The reduced ... Read More
In this tutorial, the vibrational behavior of a small aluminum plate with four waveguide structures is analyzed. This is an example of a structural component located in a device where elastic waves are propagating, like a smart speaker, an electric motor, or a MEMS device. The plate can ... Read More
This tutorial model demonstrates the use of dynamic cyclic symmetry with postprocessing on the full geometry. A 3D impeller with eight identical blades can be divided into eight sectors of symmetry. The model computes the fundamental frequencies for the full impeller geometry and ... Read More
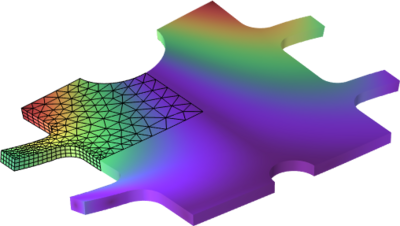
In this shape optimization example, the mass of a bracket is minimized by changing the size and position of a number of geometrical objects. The requirements give limits both on the lowest natural frequency, and on the maximum stress in a static load case. This means that results from ... Read More
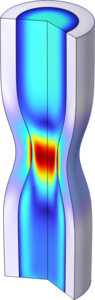
This is a benchmark model for a plane stress problem. The accuracy of the computed stress concentration is evaluated, and a mesh convergence study is performed for different element types. Read More