
Fluid flow is involved in many engineering applications. In addition to typical CFD simulations, which replace experiments in wind tunnels, flow must also be considered in the cooling of electronic devices or in the chemical industry, where reacting species are transported by a fluid. COMSOL Multiphysics offers dedicated interfaces for various flow types. When should we use the Laminar Flow or Turbulent Flow interface?
The $1 Million Problem: Understanding the Nature of Flow
The nature of flow is very complex and the governing equations — the Navier-Stokes equations — are numerically challenging.
The British applied mathematician, Sir Horace Lamb, is reported to have said: “I am an old man now, and when I die and go to Heaven, there are two matters on which I hope for enlightenment. One is quantum electrodynamics and the other is the turbulent motion of fluids. And about the former I am really rather optimistic.”
Maybe he is lucky and also got the answer to the latter one, but here on earth, it is one of the Millennium Prize Problems of the Clay Mathematics Institute. You can be rewarded U.S. $1 million if you prove that the Navier-Stokes equations, in three dimensions, have a solution and that the solution has no singularities. The proof would help us understand the nature of turbulence, which is still the biggest challenge for CFD codes.
Of course, nature always has a solution ready and we can see it in the cloud formations in the sky, the waves in the sea, and the boiling water in the pot. But, we also want a numerical solution for our applications to predict and optimize their performances. For that, COMSOL Multiphysics contains a number of interfaces that solve equations derived from the Navier-Stokes equations and are suitable for different situations.
Here, we want to give clarity on when the Laminar Flow and Turbulent Flow interface are suitable to describe some characteristic flow patterns.
Characterizing the Flow
After you choose the dimension, the first thing to consider in terms of your flow simulation is whether or not you need to take temperature variations into account. This determines whether you choose the Non-Isothermal Flow interface, where you solve the Navier-Stokes equations together with the heat transfer equation, or can neglect temperature variations and solve only the Navier-Stokes equations. That sounds easy enough. To decide if you now need to select one of the turbulent interfaces or if the laminar approach is sufficient, is not as easy.
Reynolds Number and Flow Regime
Technical applications mainly deal with forced flow. The fluid is set in motion by an external source, like a pump or fan, and enters the modeling domain with a certain velocity. Dimensionless numbers help describe the flow characteristics without starting a simulation. The dimensionless number characterizing the flow regime is the Reynolds number, which describes the ratio of inertia to viscous forces:
where \rho is the density, U is the characteristic velocity, d is the characteristic length scale, and \mu is the dynamic viscosity. Here, you can see that \mathrm{Re} is not clearly defined. What are the characteristic velocities and length scales? What if the material properties depend on the temperature?
At very low Reynolds numbers,\mathrm{Re}\ll1, the viscous forces dominate over the inertia forces. Thus, the latter may be neglected in the Navier-Stokes equations. For that, COMSOL Multiphysics contains the Creeping Flow interface. Alternatively, if you have non-isothermal flow, you can activate the “Neglect inertial term (Stokes flow)” check-box in the associated settings window.
For higher Reynolds numbers but below some critical value, \mathrm{Re}_c (the critical Reynolds number), the flow is laminar. Above \mathrm{Re}_c, it becomes turbulent. The value for \mathrm{Re}_c must be determined manually through experimental set-ups or numerical experiments for each configuration. Luckily, this is already done for typical engineering applications and can be found in related literature. But, even if you have found the value for \mathrm{Re}_c in the literature, the transition from laminar to turbulent is not immediate and there is a transitional zone where both regimes exist.
In that case, it is not obvious which approach is suitable: laminar or turbulent?
Rayleigh Number and Natural Convection
In natural convection, the flow is driven by buoyancy forces. Typically, buoyancy forces arise due to temperature differences, but concentration gradients can also be the driving mechanism. Natural convection plays an important role in geosciences. In earth’s outer core, natural convection creates earth’s magnetic field and in the atmosphere, it dictates the world’s climate.
The cooling due to natural convection (in building physics or electronic devices, for example) is often modeled using heat transfer coefficients, which were determined through experiments or numerical calculations. Modeling free convection is always a coupling of the Heat Transfer and Flow interfaces. Therefore, the Non-Isothermal Flow interface is a good choice.
The dimensionless number characterizing free convection is called the Rayleigh number, which is the product of the Grashof number, \mathrm{Gr}, the square of the ratio of viscous to buoyant timescales, and the Prandtl number, \mathrm{Pr}, the ratio of conductive to viscous timescales:
where \alpha is the thermal expansion coefficient, \Delta T, the temperature difference, and d is now the height of the layer over which the buoyancy forces are active. Similar to the Reynolds number, there is also a critical Rayleigh number, \mathrm{Ra}_c. Here, \mathrm{Ra}<\mathrm{Ra}_c means that heat is only transported by conduction. At \mathrm{Ra}=\mathrm{Ra}_c, convection becomes the dominating heat transfer process in a steady laminar flow regime. With an increasing Rayleigh number, the steady flow becomes unstable and, finally, turbulent.
Flow Regimes in Different Configurations
Now, we want to discuss the different flow regimes and which interface and study type are suitable for each.
1. Flow Around a Cylinder
With increasing Reynolds numbers, this type of flow develops a Kármán vortex street, which is a benchmark example for CFD validation without temperature variations. The Reynolds number for flow around a cylinder uses the diameter of the cylinder as the characteristic length while the material properties are constant (this is similar for other obstacles, too). Over a large range of Reynolds numbers, the flow field behind the obstacle forms periodically swirling vortices, as shown in the below example.

Stationary velocity field for \mathrm{Re}\approx 2. The flow is truly laminar and has a stationary solution. This type of flow can be solved with the Laminar Flow interface and a stationary study.
Time-dependent velocity field for \mathrm{Re}\approx 100 for 7s. The velocity field changes in space and time. With a proper mesh and time step size, this flow can be solved with the Laminar Flow interface and a time-dependent study.
A further increase of the Reynolds number will raise the frequency of the eddies and finally result in turbulent flow. Particularly in the transition regime, 3D instabilities arise and must be resolved with a 3D laminar flow interface. Once the flow gets fully turbulent, you can switch back to 2D and use a turbulent flow interface.
2. A Shell-and-Tube Heat Exchanger
The shell-and-tube heat exchanger is a common type of heat exchanger and is a typical example of non-isothermal flow with forced convection. Water flows through the tube side and air flows through the shell side of the heat exchanger. Both materials have temperature-dependent properties, which need to be considered for the calculation of the Reynolds number. The characteristic length inside the tubes is the tube diameter, but in the inlet and outlet regions, it is not clear what the characteristic length is.
It is equally unclear when it comes to the air flow around the tubes and baffles. These guide the air flow, thus increasing the amount of heat transferred between the two fluids. You can refer to literature, such as this resource, to find example calculations that provide a good estimation for \mathrm{Re}.
It is interesting to see how the Reynolds number can vary over the modeling domain. In COMSOL Multiphysics, you can plot \mathrm{Re} after the simulation. To do so, add a 3D volume plot for the water domain and enter, nitf.U*nitf.rho*0.015[m]/nitf.mu in the Expression field. Then, for every point based on the local velocity, density, and viscosity, the Reynolds number is calculated with the pipe diameter as the characteristic length. Where this length scale applies, the Reynolds number exceeds the critical value for flow inside pipes and is high enough for the flow to be turbulent.
For this case, we use a turbulent flow interface with a stationary study. This means that we do not resolve the space and time-dependent behavior of all eddies that may appear. Rather, we calculate a mean velocity field where the influence of the eddies on the heat exchanger’s properties are taken into account by additional variables.
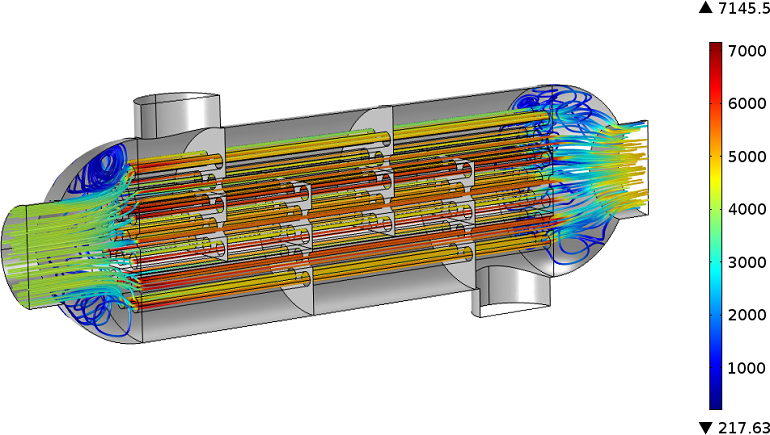
Streamline plot along the velocity field for the tube side. Colors indicate the Reynolds number.
3. Natural Convection in a Spherical Shell
The last example originates from geophysical topics and deals with buoyancy driven natural convection in a spherical shell (without rotation). When convection starts, it first forms stationary convection cells (Rayleigh-Bénard cells). This increases the buoyancy force and thereby \mathrm{Ra}, causing these cells to start to move. Finally, they break up and smaller eddies, on a shorter timescale, dominate the flow regime and turbulence arises.
The animation below shows the natural convection for a spherical shell with a buoyancy force acting in radial direction. The Navier-Stokes equations are defined with dimensionless parameters instead of material properties while the buoyancy force is expressed in terms of the Rayleigh number. The model was solved using a laminar flow approach with a time dependent study.
Starting from a linear temperature profile, buoyancy first forms symmetric convection cells, but soon an asymmetric velocity and temperature profile is obtained for Ra = 250.
Conclusion
We have examined different flow regimes and can conclude that it is not always obvious which flow interface to choose. If the dimensionless numbers \mathrm{Re} or \mathrm{Ra} are significantly smaller or larger than their critical value for the configuration, the choice is clear.
For truly laminar flow, which is often present in microfluidic devices, you would choose the Laminar Flow interface. If \mathrm{Re}\ll 1, you should choose the Creeping Flow interface.
Many industrial applications deal with high velocities and high Reynolds numbers, in which case a turbulent flow interface is required. Read our previous blog post for a detailed discussion about which turbulence model you should choose.
After all, CFD simulations are challenging and the nature of flow is still not fully understood. The COMSOL software provides interfaces to model all flow regimes using up-to-date numerical techniques. Examples from our Model Gallery (listed below) can help you get an idea of which interface is suitable for your application.
Model Downloads
- Showing natural convection with laminar flow:
- Natural convection with laminar flow:
- Buoyancy Flow in Free Fluids
- The instructions contain a detailed explanation of the dimensionless parameters and their influence on the thermal behavior
- Buoyancy Flow in Free Fluids
- Considering natural and forced convection with turbulent flow:
- Turbulent flow through a 90-degree pipe elbow:




Comments (8)
Omar Al-Rawi
February 28, 2017Hi Nancy,
Thank you for sending me this blog, which is very usefull for ones interest in fluid flow problems.
Would you mind if I ask you about the animation which represents the Time-dependent velocity field around a cylinder? Which node or/and subnode I have to use in order to create like this animation?
Thanks,
Omar
Nancy Bannach
March 8, 2017Dear Omar,
I will forward you to a tutorial video which explains it much better than I can do here.
https://www.comsol.de/video/create-export-animations-comsol-multiphysics
Best regards,
Nancy
basil Srayyih
May 30, 2018Hi Nancy,
Would you mind if I ask you about the turbulent natural convection inside a cavity filled by a pure fluid (air). Could you help me please how can I write the turbulent dynamic viscosity in the thermal conductivity place of the heat equation by using the user defined?
Thanks and best wishes.
Nancy Bannach
June 6, 2018Dear Basil,
I’m not sure I understand your question correctly. If my answer doesn’t help, please contact our support team for more elaborated discussion.
The variable name of the turbulent dynamic viscosity can be found in the Equation view of the Fluid Properties node, probably spf.muT. You can just enter this expression in the user defined edit field for the thermal conductivity. It’s just like entering any other variable or parameter name.
I hope this helps.
Have a nice day,
Nancy
Robert Gustavsson
June 9, 2022“What are the characteristic velocities and length scales?”
This remains unanswered…
Nicolas Dobler
January 31, 2024Dear Nancy
I tried to recreate the plot you showed for the shell and tube heat exchanger displaying the reynolds number on Comsol 6.2 but I keep running into the following error:
”
Undefined variable.
– Variable: nitf.U
– Geometry: geom1
– Domain: 2
Failed to evaluate expression.
– Expression: nitf.U*nitf.rho*OvenD/nitf.mu
– Plot: Volume 1
”
I checked the Equation View for the nonisothermal flow for nitf.U but it does not show up. Only the x, y and z components of the velocity field show up there. Did this maybe change in the past years while switching to newer versions of Comsol?
Best
Nicolas
Nancy Bannach
January 31, 2024 COMSOL EmployeeDear Nicolas,
the variable nitf.U, representing the velocity magnitude, does no longer exist. Some time has elapsed since the publication of this blog post, and yes you might be right that this change is due to our updated approach to setting up multiphysics models. Instead, you can now utilize spf.U, which corresponds to the velocity magnitude defined in the Turbulent Flow interface (you can find this variable in the equation view under the Fluid Properties node). This change applies to other variables in the given expression as well.
We may consider updating the blog post to reflect these changes. I will consult with my colleagues.
Best regards,
Nancy
Nicolas Dobler
February 1, 2024Dear Nancy
Thanks for the quick response. It proved to be very helpful. I figured that in ten years probably a lot changed in Comsol.
Best
Nicolas