
Today we have the pleasure of introducing Jeff Crompton, a guest author from AltaSim Technologies, who will discuss ceramic matrix composites and how to accurately analyze the production of such an advanced material.
Ceramic matrix composites (CMCs) are fast becoming popular in many industries due to their ability to withstand high temperatures, corrosion, and wear better than metal components. They are being used in space applications, burners and combustion chambers, gas turbines, brake discs, and slide bearings. The manufacture of CMCs is an inherently complex multiphysics phenomenon. Therefore, any accurate computational analysis must incorporate multiple physics that operate in a fully coupled manner. In this blog post, I will introduce you to silicon carbide-based CMCs and show you an example of how the physics can be coupled to analyze its production process.
Background of Ceramic Matrix Composites
Currently, two methods are primarily used to manufacture silicon carbide-based CMCs:
- Reactive Melt Infiltration (RMI)
- Chemical Vapor Infusion (CVI)
RMI provides relatively rapid production of near-net shape parts and is the most widely used. In RMI, a pre-form is manufactured from a porous ceramic media and liquid infiltrates the pre-form through capillary action. For CMCs of current interest, the liquid is generally in the form of molten silicon, thus leading to temperatures during manufacturing that may exceed 1,687 K. During liquid infiltration, a chemical reaction occurs between the silicon and pre-form within minutes of the liquid contacting the pre-form. Ideally, the final product takes the shape of the pre-form with full density and no porosity. In addition, silicon carbide fibers are incorporated in the pre-form as either directional fiber lay-ups or woven fiber mats, as you can see in the figure below.
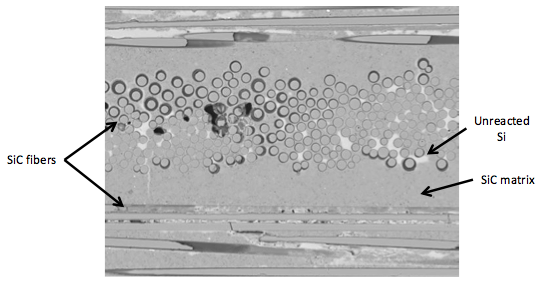
Any computational analysis of the RMI CMC production process must therefore include the following phenomena:
- Flow of fluid in a porous matrix
- Capillary fluid flow through interconnected pores
- Chemical reaction between the flowing fluid and porous matrix
- Volume changes due to the fluid-solid reaction
- Thermal transients during infiltration
- Temperature evolution on solidification and solid state phase changes
- Residual stress and distortion of components
Complex interactions and interdependencies occur between the multiple physical phenomena that introduce significant analysis challenges: unsaturated fluid flow in porous media, material deformation and physical constants that are temperature dependent, and liquid to solid transition and solid state phase changes that act as heat sources in addition to the thermal energy of the infiltrating liquid.
Example of Coupling Physics
Thermal analysis of the RMI manufacturing process for CMC production requires the inclusion of thermal effects arising from:
- Heat flux due to liquid at temperatures approaching ~1,687 K for liquid silicon
- Latent heat of fusion on solidification
- Heat of reaction for the reaction between liquid silicon and the carbon pre-form to form silicon carbide
These heat sources must be treated to provide:
- Conduction through the matrix
- Convection in the surrounding environment
- Convection in the infiltrating fluid
- Radiation to the surrounding environment
Thermal effects due to the temperature of the liquid and the phase change from liquid to solid can be easily incorporated into the standard heat transfer calculations dealing with conduction, convection, and radiation. Heat transfer from the reaction between silicon and carbon can be calculated using energy balance equations for a porous media:
in which volume averaging approaches account for the presence of a mixture of liquid and solid phases to obtain an equivalent thermal conductivity {K_{eq}} and heat capacity {C_{eq}} for the porous matrix.
The effect of the value for the heat of reaction between silicon and carbon on the local temperature distribution ahead of the reaction front is seen in the figure below and is compared against experimental measurements performed by Einset.
![]()
Predicted temperature distribution for different values of heat of reaction showing
effect of heat generation due to reaction compared to experimental measurements.
The effect of the value for the thermal conductivity on the local temperature distribution ahead of the reaction front is seen below:
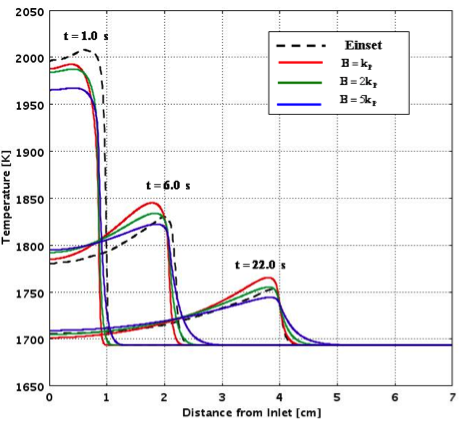
Predicted temperature distribution for different values of matrix thermal
conductivity compared to experimental measurements.
About the Guest Author
Jeff Crompton, PhD, has 20+ years of experience working with computational analysis. Together with Kyle Koppenhoefer, he started AltaSim Technologies, LLC 11 years ago to perform new product design through the application of advanced computational tools. To facilitate this goal, AltaSim Technologies became a founding member of the COMSOL Certified Consultants program, and continues to be a leader in providing COMSOL services to those interested in receiving the benefits of modeling with COMSOL Multiphysics. In addition to guest blogging for COMSOL, AltaSim Technologies also blogs about multiphysics modeling on their own website.



Comments (0)