
Superconductors are used in applications where high current density and magnetic fields are present — including electric generators, biomagnetic technology, and common products, such as fast digital circuits. Theoretically, an unlimited amount of current can flow through a wire made of a superconducting material. However, what happens to a superconductor as the current density exceeds critical limits? Let’s find out.
Critical Limits for Superconductivity
The electrical resistance of a conductive material may suddenly drop to zero when the material is cooled below a certain temperature. This is when the material becomes superconductive. Many superconducting wires are made of yttrium barium copper oxide (YBCO), a compound that displays superconductivity at relatively high temperatures (above 77 K) compared to other superconductors. Because of its material properties, it requires less power to cool down than low- or medium-temperature superconductors. However, the superconductivity only holds below a certain current density and magnetic field strength. The current and magnetic field levels at which superconductivity is destroyed are called the critical current density and the critical field. Past these levels, the material transitions back to its “normal” conductivity.

A superconducting wire like those often used in magnets. Image credit: Materialscientist.
Modeling Current Build-up
Let’s take a look at the Superconducting Wire model, which is available in our Model Gallery. This particular model was based on a suggestion by Dr. Roberto Brambilla of CESI, which is located in Milano, Italy.
The geometry is composed of two concentric circular domains representing a cross section of a wire that is infinitely extended in a direction into, or out of, our screen. The outer domain represents air around the wire, while the inner domain is assigned the material properties of YBCO.
We’ll use the Magnetic Field Formulation interface (available in COMSOL Multiphysics) to simulate changes in current density and magnetic flux over time, which is measured from the moment that current begins flowing through the wire.
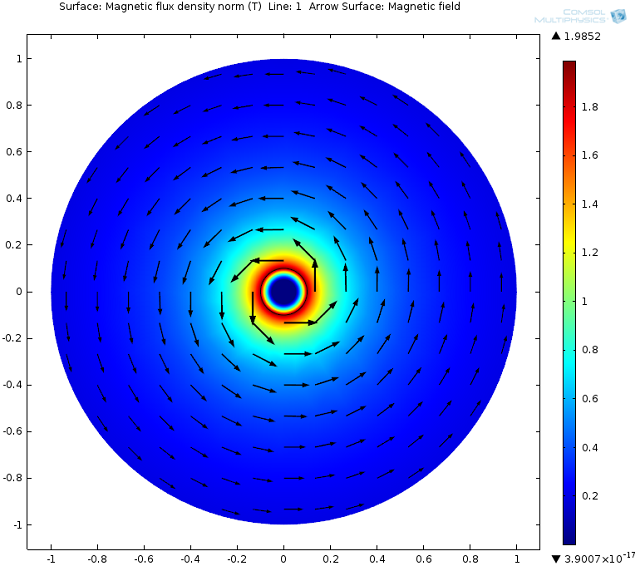
The entire geometry of the Superconducting Wire model. The wire is at the center, while the outer domain is air. These results show the magnitude and direction of the magnetic flux density.
The Magnetic Field Formulation interface uses Faraday’s law to relate the magnetic (\vec{H}) and electric (\vec{E}) fields:
Here, \vec{J} represents the current density and \mu is the magnetic permeability.
The electric field and current density are related through the resistivity, (\rho):
The magnetic field and current density are related using Ampére’s law:
If you combine all of this information, you end up with an equation where the magnetic field remains the only unknown quantity that we need to solve for:
All other quantities of interest can be derived from the magnetic field using the equations shown above. This is why we call this built-in physics interface the Magnetic Field Formulation interface. This tool is really powerful for modeling materials (like superconductors) that exhibit a nonlinear relationship between electric field and current density, which manifests as a current-dependent electrical resistivity.
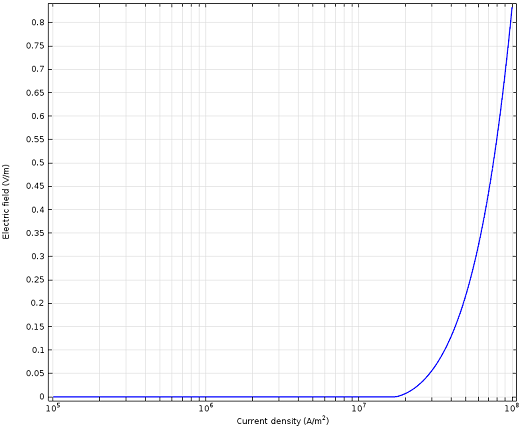
Model results showing a plot of electric field versus current density for YBCO. The current density is shown in log-scale. The electric field is zero below the critical current density of 1.7 x 107 amps per square meter, which indicates the superconducting regime of operation. The ratio of electric field to current density gives us the resistivity of the material.
In our model, we simulate a current flowing through the wire that logarithmically increases from zero to a value of 1 mega amp with a time constant of 0.02 seconds. As this is a two-dimensional model, a current flowing out of the plane of simulation is modeled by applying a circular magnetic field around the wire. This magnetic field induces a current flowing through the wire in the out-of-plane direction. The simulation illustrates the induced current building up close to critical density (for YBCO, this is 1.7 x 107 amps per square meter). As time goes on, regions of the wire lose their superconductivity because of the rising current density. This happens very quickly (in the space of less than a second). The non-superconducting region (close to the outer boundary of the wire, where the current density can become higher than the critical limit) begins to grow larger, expanding inward toward the center of the wire.
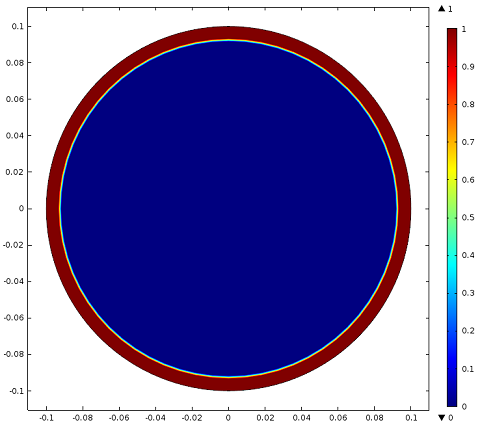
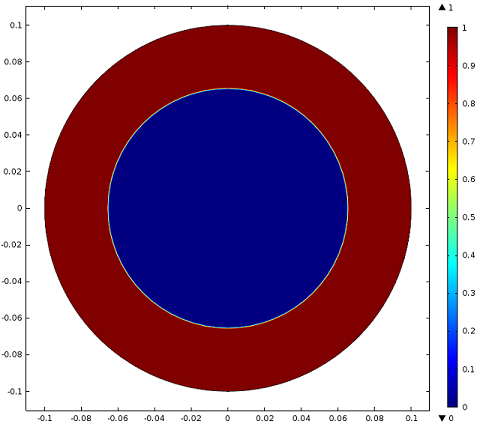
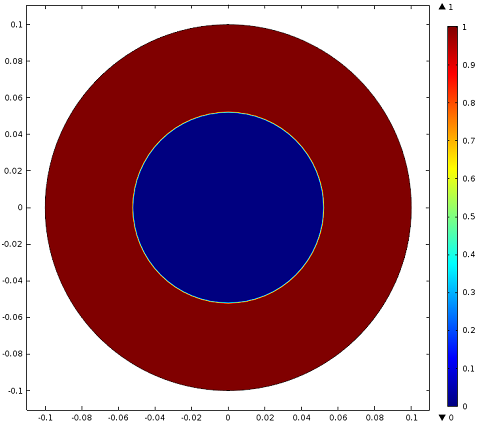
Simulation results showing where the current density is greater than the critical limit (red) in the wire for t=0.005, t=0.05, and t=0.1 seconds. After one-tenth of a second, much of the wire is no longer superconducting.
The resistivity of the wire rapidly increases due to the high current. The simulation shows that with so many amps running through it, the YBCO wire will not be usable as a superconductor. So, if you have an application with high current, make sure it stays below the material’s limit, or your superconducting wire won’t be superconducting for long.
Further Reading
Read more about the Superconducting Wire model





Comments (2)
Tosin Famakinwa
June 19, 2014Good to see example of application to superconductors in COMSOL.
Wenjia HUANG
November 26, 2018Dear Lexi,
Your example is very intuitive.
How could we change to the situation where the coil is circular?
Best regards,
Wenjia