
When modeling computationally taxing geometries, you can save time by using cyclic symmetry to cut down on memory usage. This can be more complex for rotationally than axially symmetric geometries. However, with the Structural Mechanics Module you can easily solve a single section of an impeller model and still get accurate results.
Fluid-Structure Vibration Analysis for Cyclic Symmetric Structures
When analyzing turbines and compressors, it is important to have an understanding of vibration within the system. In turbomachinery, blade vibrations induced by the load of the fluid flow can ultimately cause failures. Therefore, conducting an eigenfrequency analysis on these types of geometries is important. Typically, structures of this nature have rotational symmetry and can be split into repeating sections. It follows that cyclic symmetry can be used to reduce computational requirements.
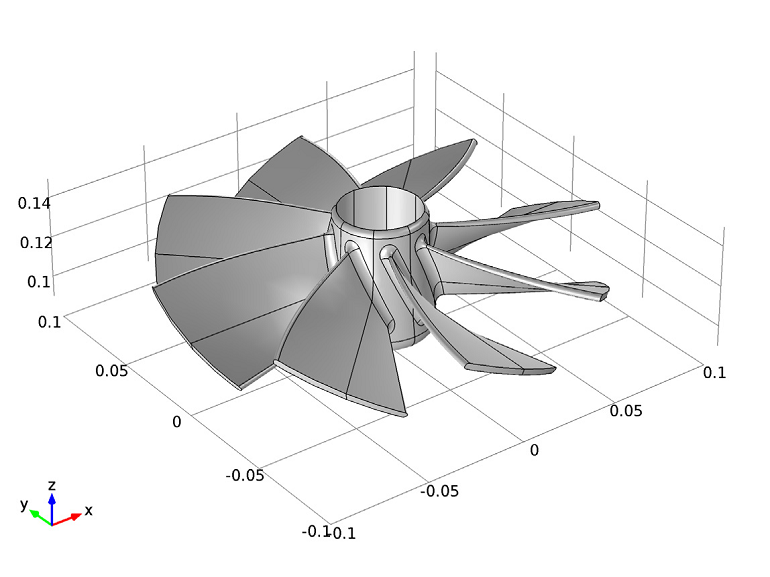
Geometry of an impeller.
Introducing the Model
The Vibrations of an Impeller model, available for download from the Model Gallery, compares the results of the analysis of one section of the geometry with the results for the full impeller geometry. The COMSOL software offers a predefined functionality available in the Solid Mechanics interface for setting up cyclic symmetry conditions (found under the Periodic Condition Boundary feature). The impeller geometry is divided into eight identical sections, as shown below.
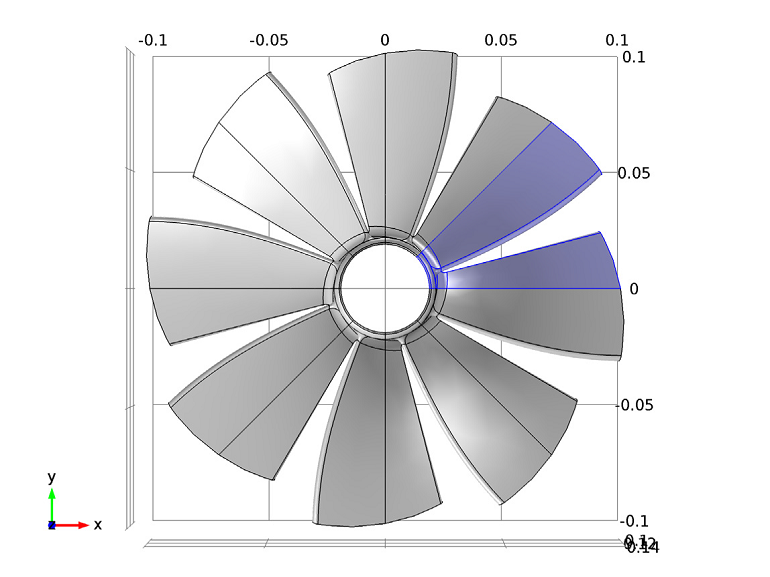
The interface uses the Floquet theory, which translates the periodic system into a traditional linear system. Floquet periodicity conditions are used at the sides of the sector of symmetry to prevent cyclic decomposition.
Setting Up the Model
The eight sections are represented as a sector with the angle θ = π/4. The impeller is mounted on a shaft that is modeled as a fixed constraint and the possible effects of the rotation of the shaft have been ignored. From here, you can conduct an eigenfrequency analysis study. You can perform the analysis on one sector of symmetry by using an angle of periodicity of ϕ = mθ for the cyclic symmetry of the eigenmodes.
In this equation, the mode number, m, can vary between 0 and N/2, where N is the total number of sections so that θ = 2π/N. You can perform a sweep over the required values of the cyclic symmetry parameter to accurately recover all the eigenfrequencies of the full model.
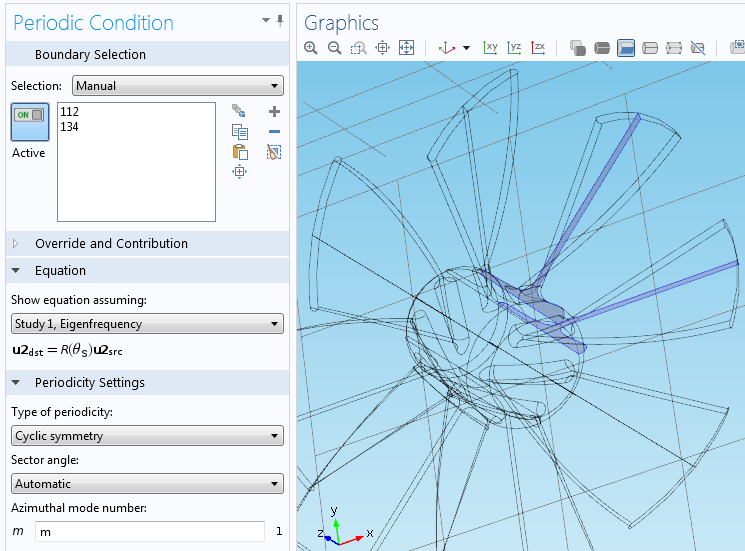
The settings window for Periodic Condition with Cyclic symmetry.
There are actually several other types of periodicity that can be employed when you need to reduce model sizes for periodic structures.
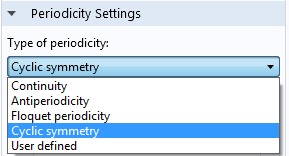
The different periodicity conditions.
Frequency Response Analysis Results Agree
You can also conduct a frequency response analysis of both the sector of periodicity as well as the full impeller geometry. The results can be visualized by using the results computed for one sector over the full geometry. This is done using a predefined type of derived dataset called Sector 3D, which can be found under the Results in the COMSOL software. You can see the frequency response analyses below:
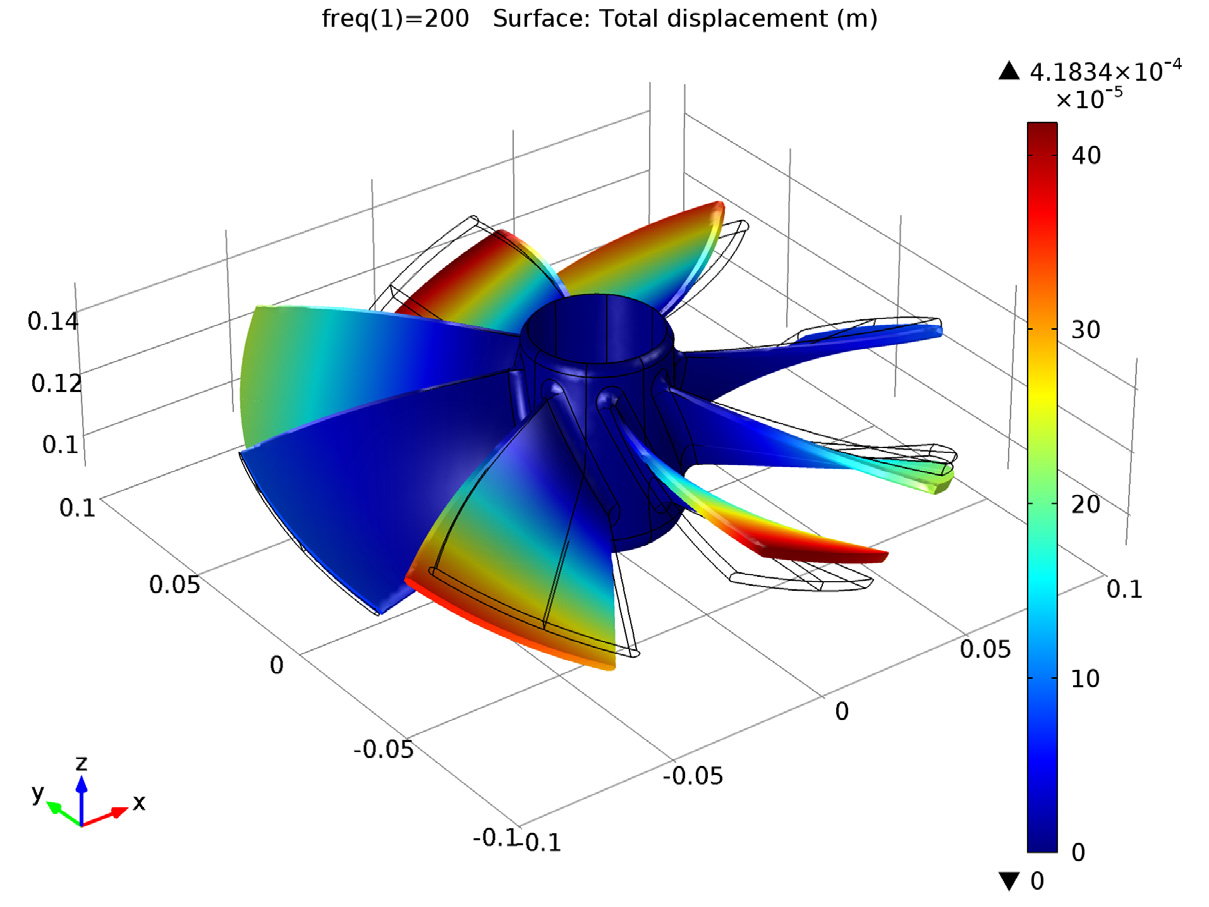
Frequency response computed on the sector of periodicity only, and then visualized over the full geometry.
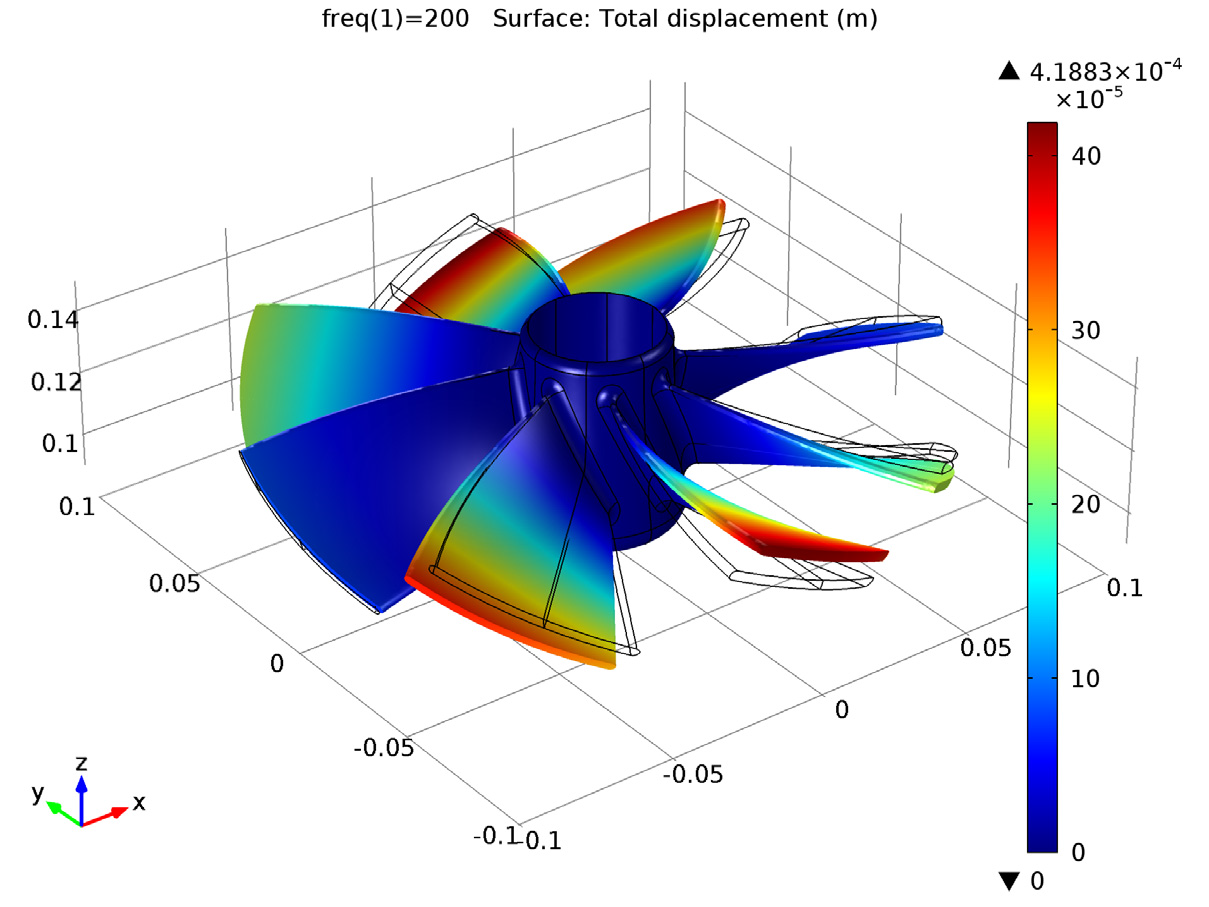
Frequency response computed for the full geometry.
As we can see, there is very good agreement between the results, demonstrating that using cyclic symmetry to reduce the geometry will not compromise the accuracy of the results.
Further Reading
- Model Download: Vibrations of an Impeller
- Knowledge Base Entry: Using Symmetries in COMSOL Multiphysics



Comments (1)
David Chen
October 5, 2015I would like to know more about applying symmetry on the model