
A couple of weeks ago, we published the first blog post in a Hybrid Modeling series, about hybrid parallel computing and how it helps COMSOL Multiphysics model faster. Today, we are going to briefly discuss one of the building blocks that make up the hybrid version, namely shared memory computing. Before that, we need to consider what it means that an “application is running in parallel”. You will also learn when and how to use shared memory with COMSOL.
Multicore and Multithreading
The hunger for faster computers is ever increasing, but larger computational requirements in an era of certain technological limitations (like the increase of clock speed) forced the computing world to go multicore. Multicore computers are nowadays mainstream. Modern multicore processors usually feature up to 12 cores, but can have even more than 60 cores (to see what a core is and how it relates to shared memory computing, check out the diagram about shared memory computing on this page).
Consequently, every application needs to account for parallelism in order to exploit the capabilities of recent parallel hardware. Otherwise, they would just be computing on one of the cores. As a user, you are often not directly affected by parallelism, but you should be aware of the parallel power on your desktop, the software settings that could possibly be changed to improve productivity, and the expectations you should have when ramping up all available cores.
In order for an application, which executes a process, to be able to be run in parallel on a multicore machine, it has to be split up into smaller parts and these smaller parts are called threads. The execution of several of those threads seemingly in parallel is called multithreading, and this has been a built-in function in our desktop computers for the last 15 years or so. Multithreading does not necessarily require multiple cores and can be performed on a single-core machine by quickly switching between the active threads in time-slicing mode. This over-assignment allows for better resource utilization and can also be used when multiple cores are available.
Now, it is easy to understand why a multicore processor is a large step forward in comparison to a single core. Having multiple computational units means that we can run multiple threads at the same time. It is accordingly possible to perform more work per time unit. As a result, parallelization is now the major source for speeding up computations.
In the figure below you can see how COMSOL Multiphysics can benefit from an eight-core machine. Computational times are significantly reduced when all eight cores are used. As a direct benefit, you can run many more simulations in the same amount of time — increasing productivity. For the selected model below, productivity has increased by a factor of 6.5 on an eight-core machine.
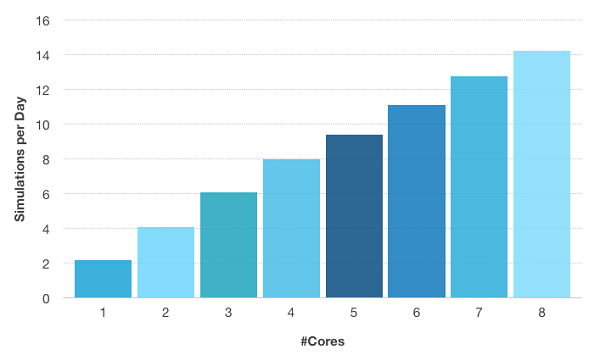
Number of simulations per day with respect to number of cores used for the RF heating model depicted below. The compute server used was equipped with 2 Intel® Xeon® E5-2609 and 64 GB DDR3 @ 1600 MHz.
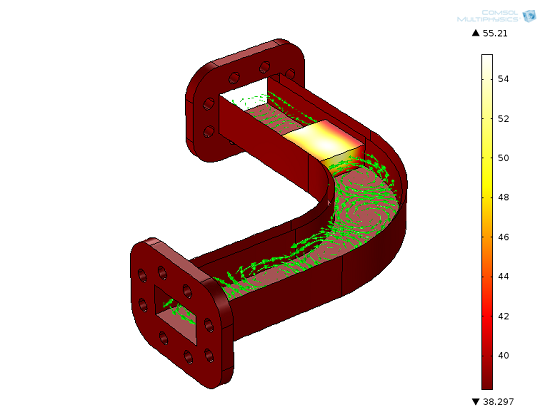
The model for which the speed-up was obtained. The red-to-white scale denotes temperature in degrees Celcius and the green arrows show the magnetic field. The model has almost 1.4 million degrees of freedom, and was solved with the PARDISO direct solver requiring 52 GB of RAM. Note that this is a two-way coupled multiphysics model. A smaller version of this model is available in the Model Gallery.
What is Shared Memory?
When a process is executed on a computer, the operating system gives a certain amount of memory to the application to play around with (note: in COMSOL Multiphysics you can see the amount of memory allocated by the application in the toolbar at the bottom). This memory is, broadly speaking, shared between all of the threads that are created by its mother process, and each thread has access to all of the variables that are stored therein.
As an analogy, one can think of a conference room table around which a meeting is taking place. All of the reports and information that are important for the meeting are spread out on the table in front of the participants. Each participant can read or write on any paper he wants to. Hence, the information is shared while every participant can pick his own piece of work.
As most analogies, this one simplifies the real concept a lot, and it only gives us a hunch as to how shared memory works in principle. There is much more to keep in mind when working with shared memory programming on a computer. It is apparent that some synchronization mechanisms need to be used and that resource contention may appear, when, for example, 50 people are writing on the same sheet of paper. This is also a first explanation as to why the speed-up in the first figure, above, tapers off and would reach saturation at a certain point.
The sharing of memory allows for direct access to the variables that are shared, and the program does not have to communicate to send information from one thread to another. Since communication can be a large bottleneck and should be avoided where possible, this is an advantage with COMSOL software. There are, of course, drawbacks with shared memory computing. As we mentioned in the earlier blog post, the amount of memory we can use is confined to what we have available in the machine, and there are other logistical problems that the programmer has to consider when programming the application.
Why Use Shared Memory?
As mentioned before, parallelization is the major resource for speed-up. Hence, the programmer needs to work out how the overall work can be shared between all participating threads. This is straightforward in the case of tasks that can be executed in parallel without any dependencies.
In numerical linear algebra, you are typically performing work on huge arrays like matrices and vectors. The most common construct here are long loops over the arrays. In a shared-memory approach, the whole array is accessible by all threads and the loop can be split among the threads in many fashions (if there are no loop-carried dependencies). COMSOL Multiphysics takes advantage of shared memory parallelism for all kinds of linear algebra operations and for specific algorithms — giving you a versatile parallel tool.
However, there are tasks and algorithms where it is difficult or even impossible to take advantage of a parallel computing approach. One such example is the Fibonacci series, F(n) = F(n-1) + F(n-2), which is a non-parallelizable recursive problem, where each step depends on the previous one. Other algorithmic parts that do not fully benefit from parallel computing and multicore computers are, for example, time-stepping schemes and continuation (like ramping) studies where the order of computation is fixed.
However, few of us use our computers and numerical software to compute elements of the Fibonacci series all day long, and luckily solving a system of linear equations, which is a large part of every finite element analysis software, is a problem that is parallelizable to quite a large extent. Therefore, more or less every problem where a matrix has to be solved benefits from multicore computers, even if the matrix equation is just a part of the larger task, such as a time-dependent problem. Since COMSOL Multiphysics is primarily computing matrix-vector operations in the vast majority of models, there are huge advantages in using shared memory on multicore processors. For time-stepping schemes and continuation studies, every time and parameter step itself can be performed in parallel. To achieve scalability for these types of studies, the underlying physics that is subjected to the time-stepping or continuation study should contain a sufficiently large number of degrees of freedom.
Moreover, you have to keep in mind that the overall speed-up is limited by the non-parallel fraction of the algorithm and its implementation. This well-known observation is described by Amdahl’s law. By extrapolating the non-parallel fraction in the model above, we find that even on a machine with an infinite number of cores, the increase in speed-up cannot exceed much more than a factor of 30 (which is still impressive!). This would result in slightly more than 60 simulations per day.
How COMSOL Multiphysics Takes Advantage of Multicore
The optimal performance of numerical simulations on multicore computers, of course, relies on the fact that all cores are in use. By default, the COMSOL software utilizes all available cores on your system, so there is nothing specific to be done in order to squeeze out the best from your system.
However, there may be scenarios where you would like to measure the speed-up of your model or your system, or you would like to keep some of your cores for other applications or tasks. In this case, you can control the number of cores to be used when starting up COMSOL Multiphysics, or by editing the Preferences settings for Multicore and Cluster Computing. Moreover, in hybrid parallel computing, it might be beneficial to use specific settings when using distributed memory and shared memory at the same time.
Check back soon, as we will cover this topic in the next blog post in this series.
Further Reading
- As I mentioned in the previous blog post in this series, a good tip for those who want to further read up on the details behind shared memory computing is the Lawrence Livermore National Laboratory’s; Introduction to Parallel Computing.
- Keep up with the Hybrid Modeling blog series by bookmarking this page.





Comments (0)