In this final installment of our Chemical Kinetics series, we will look at one of the major chemical syntheses of the modern era. This is a process that every single one of us has benefited from, whether we know it or not: ammonia synthesis. It has become one of the most studied reactions in history, its intricacies and complexities are the subject of several textbooks, and its history is a complex tale of good and evil.
Water, Water Everywhere, Nor Any Drop to Drink
Ammonia, with its four atoms, is an incredibly simple molecule:
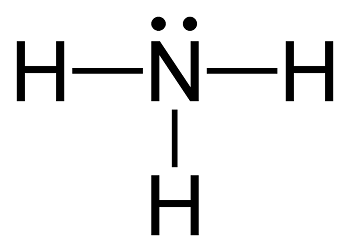
Despite this simplicity, its large-scale industrial production from its constituent elements — nitrogen and hydrogen — was, and remains, a great scientific challenge. The balanced equation of the synthesis, again, deceptively simple, can be written as:
N2 + 3H2 → 2NH3
Hydrogen reacts with nitrogen to form ammonia. Hydrogen gas is readily available from fossil fuels, or from electrolysis of water. As for nitrogen, it is readily available… well, all around us. In fact, the very air you are breathing right now contains four nitrogen molecules out of every five!
So, what’s the problem? Why were not one, but two Nobel Prizes awarded for ammonia synthesis? As always in science, the devil is in the details. It turns out that nitrogen, one of our reactants, is an incredibly stable molecule. It is frequently used in the laboratory as an inert gas.
Its resistance to reaction can be attributed to its structure:
N≡N
The triple bond is extremely strong, so breaking it requires very high temperatures (reactions of N2 have high activation energy). If you have been following the Chemical Kinetics series, you might be able to guess the solution: you use a catalyst to lower the activation energy (we discussed biological catalysts in the last post of this series).
The synthesis of ammonia is known as the Haber or Haber-Bosch process, which is named in honor of the chemists who developed the first effective catalysts. The production catalyst, which is made of iron and iron oxide with various other additional compounds, was first used on bulk scale in 1913 and is still commonly used today. This is an active and cheap solution that allows the process to be performed directly at an appreciable rate.
Ammonia Production
It is telling that significant research on ammonia synthesis was performed during the years leading up to World War I. A short digression on why we would want to produce ammonia will inform you about the industrial importance of the process.
The Darker Side of the Coin
In a word: explosives. Ammonia is a precursor compound in the manufacturing of a large number of explosive substances that have been in use for centuries.
Before the era of industrial ammonia synthesis, these precursors were usually imported from countries rich in guano (bird and bat droppings). Guano was abundant in Latin America and had a geopolitical importance comparable to petroleum in the present era.
Wars were waged over the control of guano-rich regions. When the sea routes to the German Empire were sealed off by the Entente Powers, it effectively put a limit to the duration of World War I. Without guano, the production of explosives would have had to come to an end. The industrial, large-scale production of ammonia in Germany led to a prolongation of fighting and destruction in Europe.
All is not dark in the world of ammonia production, however. There is another — lighter — side to the story.
The Lighter Side of the Coin
Ammonia is also used for another vital purpose: fertilization. Nitrogen compounds are required for the growth of plants and animals. Remember that proteins consist of amino acids. The “amino” part of the name is due to the nitrogen-containing group.
Until less than a century ago, agricultural output was limited by nitrogen-rich, “naturally occurring”, fertilizer, which can be viewed as the mammalian equivalent of guano. In the past, there was a very real fear of global famine because there was just not enough fertilizer available to ensure the necessary agricultural output for global food security.
The synthesis of ammonia changed all of this. Our world can, at present, sustain a much larger number of people thanks to industrially-synthesized fertilizers. It is now estimated that nearly 80% of the nitrogen atoms found in human tissue have passed through the industrial production of ammonia.
From here, we will ignore the good and bad of producing ammonia, and move straight to considering the chemical engineering involved by simulating ammonia synthesis with COMSOL Multiphysics.
Ammonia Synthesis Process Conditions
It comes as no surprise that ammonia production is one of the best understood chemical processes. Countless scientific publications and textbooks have been written on the subject. Considering a global production that exceeds 200 million tons per year, even seemingly minor process improvements will yield great economic benefits.
Ammonia synthesis is an exothermic (heat-releasing) reaction because the combined bond strength of the six N-H bonds, in the products, is greater than the combined bond strength of the one N≡N and three H-H bonds in the reactants. Exothermic reactions are, thermodynamically, less-favored at higher temperatures. However, we need high temperatures, even with a catalyst, to overcome the significant activation energy. In fact, ammonia synthesis is a perfect example of a delicate balance frequently encountered in chemistry: the kinetics (rate) of the reaction would profit from higher temperatures, but the thermodynamics (yield of product at equilibrium) would be more advantageous at lower temperatures.
These subtleties suggest that modeling may help us find optimal conditions. Since the process is well understood, a high-fidelity of modeling is demanded by the chemical industry, and so the equations describing ammonia process design are very detailed and highly non-ideal (and as a consequence, extremely nonlinear). At the pressures and temperatures typically used to produce ammonia (around 400°C and 200 bar), chemicals behave quite differently from the way that the mass action and ideal gas laws would have us expect.
One of the many known kinetic rate expressions, for instance, is written as:
(1)
Here, k refers to the Arrhenius rate constant, K_a to the equilibrium constant, a_i to the activity of species i, and \alpha to an empirical constant that is usually between 0.5 and 0.75 in literature.
For the equilibrium constant, K_a, the following expression has been empirically derived as a function of temperature, T, in units K:
(2)
{\log _{10}}{K_a} = – 2.691122\;\log T – 5.051925 \cdot {10^{ – 5}}{\mkern 1mu} T\\
+ 1.848863 \cdot {10^{ – 7}}{\mkern 1mu} {T^2} + \frac{{2001.6}}{T} + 2.689
\end{array}$
The activities can be determined from the fugacity coefficients, \phi, via:
(3)
where x_i is the component mole fraction and P is the system pressure.
The fugacities themselves also depend on empirical equations. These expressions quickly become extremely unwieldy. Take, for instance, the expression for hydrogen:
(4)
\phi_\mathrm{H_2} &=\exp \left\{e^{-3.8402\,T^{0.125}+0.541}P-e^{-0.1263\,T^{0.5}-15.98}P^2\right.\nonumber\\
&\qquad \left. {}+300\left[e^{-0.011901\,T-5.941}\right]e^{-\frac{P}{300}}\right\}\nonumber
\end{align}
Besides violating any aesthetic sentiment, you can see that we have no hope of solving these equations by hand. An expression like this is extremely nonlinear and may cause difficulty in the computation. The difficulty doesn’t stop there, however. The rate expression must also be multiplied with a catalyst-dependent efficiency factor, \eta, to account for the mass transport to the interior of the catalyst:
(5)
The efficiency factor is computed from the empirical correlation, below (with Z as the conversion):
(6)
The b coefficients are known at three different pressure values and must be interpolated between these.
As if the problem wasn’t already complex enough, the significant heat released by the exothermic reaction means that the energy balance must be solved together with the mass balance. The reaction enthalpy also depends on the pressure and temperature — as do the heat capacities for all involved species.
In short, we are presented with a relevant problem involving several equations, complex nonlinearities, and couplings between heat and mass conservation. In other words, an ideal playground for COMSOL Multiphysics.
Incorporating Good Data into Your Simulations
Fortunately for us, heat capacity and reaction enthalpy data can both be readily obtained from the National Institute for Standards and Technology (NIST) WebBook in a very useful, exportable, format. Even more fortunate, this exported data, in a simple tabulated format, can be imported directly into COMSOL Multiphysics.
Take, for example, the heat capacity data for ammonia. One can either choose the NIST option or input an empirical function derived in the 1980s:
(7)
where the molar heat capacity is expressed in J/mol/K.
Given the choice between typing out an equation, like the above, and importing benchmarked and tested data from NIST — a matter of just a few clicks in COMSOL Multiphysics — the import wins, hands down. Accordingly, all heat capacities were simply imported into the software and applied without any further refinement:
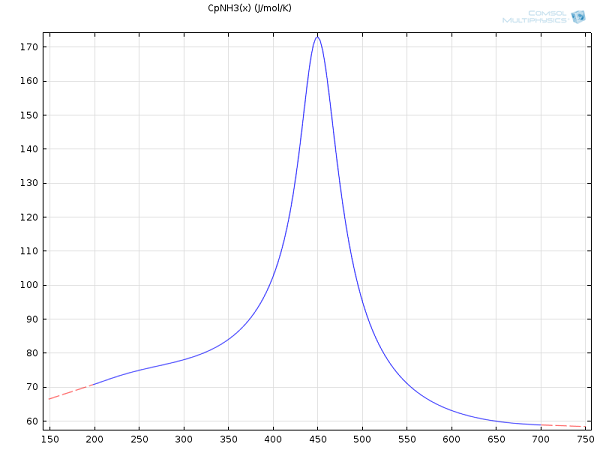
Interpolated heat capacity for ammonia from the NIST WebBook.
Modeling Strategy and Results
Once all the relevant data has been imported into COMSOL Multiphysics, setting up the reaction kinetics is a breeze.
We have chosen the Ammonia Synthesis PFR model (available in our Model Gallery), so we can compare it to an existing benchmark (Rase, H. F: Chemical Reactor Design for Process Plants, Volume 2: Case Studies and Design Data, 1977).
By using a steady-state plug flow reactor model, where time is utilized for stepping along the length of the reactor (called 0D in the COMSOL software) and an intermediate pressure, we can bypass the expensive CFD calculation and leave it for a more detailed analysis. We can incorporate an energy calculation into the reaction system with the “Energy Balance” node.
Here are some results for yields and reactor temperature:
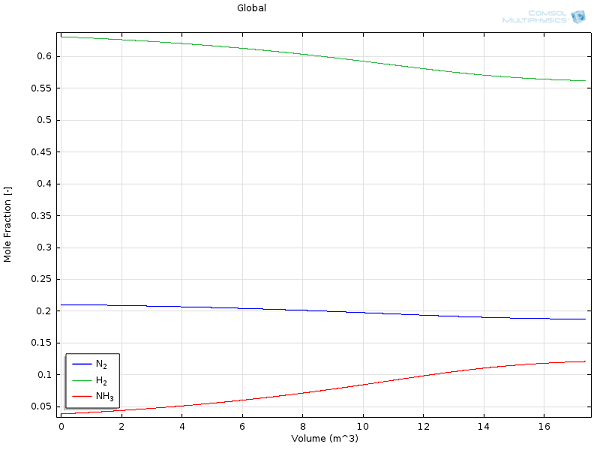
Mole fractions for hydrogen (green), nitrogen (blue), and ammonia (red) as a function of reactor extent.
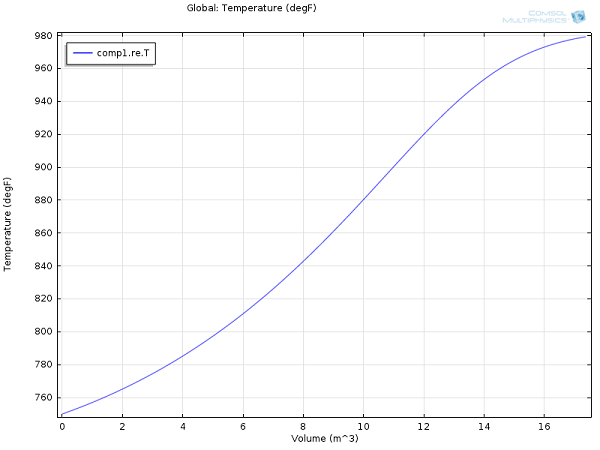
Temperature profile within the ammonia conversion reactor.
While the figures do serve to make a point regarding the descriptive power of the model, nothing beats numbers when comparing with existing benchmarks.
For the same process conditions as applied in this COMSOL Multiphysics model, Rase obtains a final ammonia mole fraction of 13% and an outlet temperature of 970°F (essentially the same values we obtained here at a fraction of the effort).
While this 13% outlet fraction may seem low at first glance, the balancing act between thermodynamics and kinetics (as mentioned above) is responsible for such a low-equilibrium composition. Because the separation of the product from the substrates is easily and efficiently accomplished, large recycle-loops are industrially applied. The unreacted nitrogen and hydrogen gases will be distilled from the mixture and returned to the reaction vessel, making ammonia synthesis one of the most efficient and highly-optimized chemical processes.
Conclusions and Next Steps
This concludes our Chemical Kinetics series. Today, we discussed chemical reaction engineering for a highly complex and nonlinear process. We also simulated one of the most important processes in the world — ammonia synthesis — with COMSOL Multiphysics and compared our results to an existing benchmark.
While this analysis is only meant to provide an initial overview of ammonia synthesis, it shows the great potential and power the COMSOL software can provide to relevant (and sometimes world-changing) chemical technology.
- Read more about the Ammonia Synthesis PFR model
- Learn more about the software:
- Try COMSOL Multiphysics first-hand



Comments (6)
Ivar Kjelberg
May 10, 2014Hi Eyal
And thanks for an interesting article, with nice historical references, an interesting non linear process indeed. Probably next time you will add some Plasma Physics and talk about the Birkeland–Eyde process 🙂
Sincerely
Ivar
Eyal Spier
May 15, 2014 COMSOL EmployeeHi Ivar,
Thanks a lot – I enjoyed writing it! I like your idea about the Birkeland-Eyde process, I will start investigating it!
All the best,
Eyal
Ghassan Chehade
February 13, 2017Hi Eyal,
The article was interesting and helpful. I am having trouble accessing the ammonia synthesis PFR model as it is not found in the library. I hope you would have a pdf file for modeling instructions?
Thanks,
Ghassan
Caty Fairclough
February 14, 2017Hi Ghassan,
Thank you for your comment! I apologize for the inconvenience, but this model is not available at the moment. Please feel free to contact support if you have any questions related to your modeling processes.
Online support center: https://www.comsol.com/support
Email: support@comsol.com
Best,
Caty
Mohaimin Islam
March 3, 2019Is the pdf file with modeling instructions of the ammonia converter available?
Brianne Christopher
March 11, 2019 COMSOL EmployeeHi Mohaimin,
Thank you for your comment. That model is currently unavailable.
For questions related to your modeling, please contact our Support team.
Online Support Center: https://www.comsol.com/support
Email: support@comsol.com
Thank you,
Brianne