
Previously in this blog series, my colleague Pär described parallel numerical simulations with COMSOL Multiphysics on shared and distributed memory platforms. Today, we discuss the combination of these two methods: hybrid computing. I will try to shed some light onto the various aspects of hybrid computing and modeling, and show how COMSOL Multiphysics can use hybrid configurations in order to squeeze out the best performance on parallel platforms.
Introducing Hybrid Computing
In recent years, cluster systems have become more and more powerful by incorporating the latest multicore technologies. Parallelism now spreads out across several levels. Huge systems have to deal with parallelism across nodes, sockets, cores, and even vector units (where operations are performed on short vectors or 1D arrays of data, not on scalar values or single data items).
In addition, the memory systems are organized into several levels as well. And as these hierarchies get deeper and deeper and more complex, the programming and execution models need to reflect these nested configurations. It turns out that it is not sufficient to deal with just a single programming and execution model. Therefore, computing is becoming increasingly hybrid.
Core’s Law and Clusters
Multiple computing cores are ubiquitous and everyone needs to deal with parallelism. As clock frequencies have stalled at a high level of around 2-5 GHz, the ever increasing hunger for computing power can only be satisfied by adding more and more cores. The well-known Moore’s law has turned into a corollary Core’s law — stating that the core count per die area will keep on increasing exponentially.
A direct consequence of this development is that the resources per core (e.g. the cache memory and number of memory channels) will become smaller due to logistics. The latest multicore incarnations, of the classical CPU-type, have up to sixteen cores but only up to four memory channels.
Typically, several multicore CPUs are providing highly capable shared memory nodes that bring impressive computing power in terms of GigaFLOP/s (i.e. billion floating point operations per second). Several of these shared memory nodes are then integrated into clusters via high-speed interconnects — providing nearly unlimited resources in terms of (Giga/Tera/Peta)FLOP/s and memory capacities. The only limits are your IT department’s budget and floor space.
These days, a cluster system needs to have more than 100,000 cores in order to receive a high ranking in the recent TOP500 list.
Reaching the Limits
A cluster represents a distributed memory system where messages are sent between the nodes by means of message passing. Here, the Message Passing Interface (MPI) with several open source and commercial implementations is the defacto standard. Typically, inside the node, OpenMP is used for shared memory programming.
Yet, numerical experiments easily unveil the limitations of multicore platforms: it is getting more and more difficult to feed the beasts. Put plainly, it is hard to get as much data to the cores quickly enough to keep them busy and crunching numbers. Basically, you could say that FLOP/s are available for free but you must keep an eye on the computational intensity, i.e. the number of FLOP per data element — a characteristic of the algorithm. The computational intensity is providing an upper bound for the achievable FLOP/s-rate.
If the computational intensity is increasing linearly in problem size, the bandwidth is not limiting performance. But the typical operation for finite element numerical simulations is of sparse matrix-vector type, which is bandwidth-bound, and the bandwidth is typically proportional to the number of memory channels in a multicore system. Once the available memory bandwidth is saturated, turning on more and more cores has no added value. This is the reason why speedups on multicore CPUs and shared memory platforms often saturate as the memory traffic is already at a maximum level, even though not all cores are being used for computations. Cluster systems, on the other hand, have the additional benefit of increased accumulated bandwidth and therefore better performance. (For further details about bandwidth limitations exemplified by the STREAM benchmark go here.)
On the hardware side, attempts have been made to mitigate the bandwidth limitations by introducing a hierarchy of caches. These can range from small level-1 caches, restricted to a single core with only a few hundred KB of memory size, to up to big level-3 caches, shared between several cores with up to a few dozen MB of memory size. The aim of the caches is to keep the data as close to the cores as possible, so that data that is to be reused does not need to be transferred from the main memory over and over again. This removes some of the pressure from the memory channels.
Even a single multicore processor itself can bring about a nested memory hierarchy. Yet, packaging several multicore processors into multiple sockets builds a shared memory node with non-uniform memory access (NUMA). In other words, some parts of the application data is stored in memory local to a core and some of the data is stored in remote memory places. Therefore, some parts of the data can be accessed very fast while other accesses have longer latencies. This means that the correct placement of data and a corresponding distribution of compute tasks are critical for performance.
Being Aware of Hierarchies on Performance
We have learned that shared memory systems build up a hierarchical system of cores and memories and that the programming model, algorithms, and implementations need to be fully aware of these hierarchies. As the computing resources of a shared memory node are limited, additional power can be added by connecting several shared memory nodes by a fast interconnection network in distributed computing.
To bring back our previous analogy from the shared memory and distributed memory computing blog posts, we are now using a variable number of conference locations to represent the cluster, where each location provides a conference room with a big table to represent a shared memory node.
If the overall work to be done increases more and more, the conference manager can call other locations of the company for help. Suppose the conference rooms are located in Boston, San Francisco, London, Paris, and Munich, for instance. These remote locations represent the distributed memory processes (the MPI processes). The manager can now include new locations on demand, such as adding Stockholm — or in terms of hybrid computing, she can set up additional processes (i.e. conference tables) per shared memory node (i.e. per conference room location).
Each conference room location (process) has a phone on the table in the meeting room, which employees can use to call any other location (another process) and ask for data or information (message passing). The local staff (a limited resource) is sitting around each conference table in a particular location. Every employee at the conference table represents a thread that helps solving the tasks at the conference room table.
On the table, local data is available in a report (level-1 caches), in folders (level-2 caches), in folders located inside cabinets (level-3 caches), in the library on the same floor (main memory), or are filed in the archive in the basement (hard-disk). Several assistants (memory channels) are running around in the building in order to fetch new folders with requested information from the library or the archive. The number of assistants is limited and they can only carry a limited number of folders at the same time (bandwidth).
Having more people at the table does not add any value if there are no more assistants available who can bring them enough data to work with. It is clear that the conference manager needs to make sure that the data necessary for the work is available on the table and that all the employees in the room can contribute effectively to reach a solution to a given problem. She should also make sure that the number of calls to other conference locations via the phone on the table is kept at a minimum. In terms of numerics, the implementations should be hierarchy-aware, data should be kept local, and the amount of communication should be kept at a minimum.
The phone calls between conference locations represent MPI calls between processes. On the meeting room table, a shared memory mechanism should be employed. In total, a perfect interplay of distributed memory (MPI) and shared memory (OpenMP) is required.
Example of a Hybrid Cluster Configuration
Let’s take a closer look at some possible cluster and core configurations. In our test benchmark model below, we investigated a small cluster that is made up of three shared memory nodes. Every node has two sockets with a quad-core processor in each socket. The total core count is 24. Each processor has a local memory bank, also illustrating the NUMA configuration of main memory.
Now, we test the cases where three, six, twelve, or twenty-four MPI processes are configured on this cluster. With three MPI processes, we have one MPI process per node and eight threads per MPI process that can communicate via shared memory/OpenMP inside the node and across the two sockets of the node. With six MPI processes we would have one MPI process per socket, i.e. one per processor. Each MPI process then needs four threads. The third possibility of twelve MPI processes is to set up two MPI processes per processor with two threads each. Finally, we can test one MPI process per core totaling to twenty-four MPI processes on the system. This is the non-hybrid case, where no shared memory parallelism is needed, and all communication occurs through distributed memory.
Which configuration do you think is the best one?
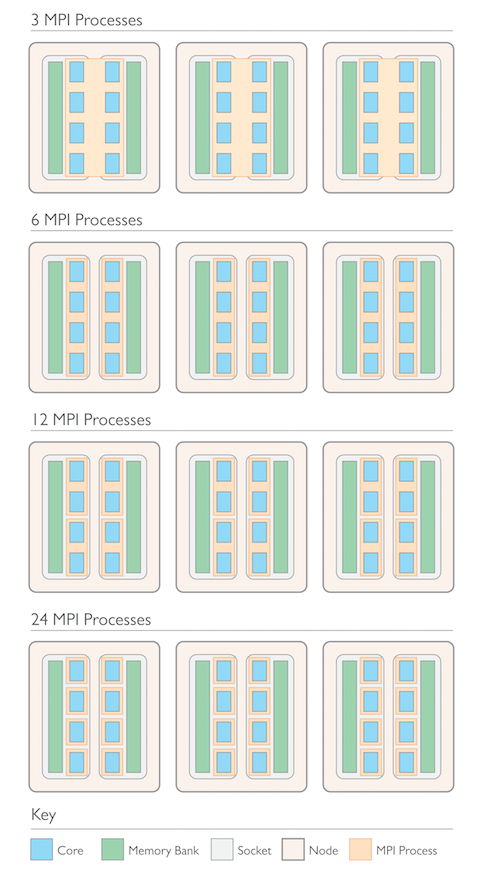
Different MPI configurations on a cluster with three shared memory nodes consisting of two sockets, each with a quad-core processor and local memory banks.
Why Hybrid?
Why not use a single programming and execution model and ignore the hierarchical core and memory configuration? First of all, it’s because shared memory (OpenMP) mechanisms cannot be used globally on standard type systems with standard installations (no world-spanning table is available to share the data).
So why not use message-passing globally across all cores — with 24 MPI processes as in the example above? Of course it would be possible; you can use message-passing even between cores on the same shared memory node. But it would mean that every employee, in our analogy above, would have his or her own phone and would have to make calls to all other employees worldwide. There would be problems of engaged signals or people put on hold and, as a result, not working.
In fact, the real scenario is more complex because modern MPI implementations are well aware of hierarchies and are trimmed to use shared memory mechanisms for local communication. One of the downsides of MPI is that memory resources are wasted quadratically in the number of participating processes. The reason for this is that internal buffers are set up where the data is stored (and possibly duplicated) before the actual messages can be sent between the processes. On 106 cores, this would require 1012 memory buffers for a single global communication call (if the MPI implementation is not hierarchy-aware). In hybrid computing, the number of MPI processes is typically lower than the core count — saving resources in terms of memory and data transfers.
Another big advantage of using the hybrid model is that many mechanisms (like data placement, thread pinning, or load balancing, to name a few) need some dedicated actions of the programmer. The hybrid model provides a much more versatile tool to express these details. It shares the advantages of a global and discrete view of the memory. It is a natural choice to consider the hybrid OpenMP + MPI model since it fits with the hybrid structure of memory and core configurations, as illustrated in the figures.
Most importantly, the hybrid model is flexible and adaptable and helps reduce overheads and demands for resources. In terms of finite element modeling, hierarchies in the data and tasks can often be derived from the physical model, its geometry, the algorithms, and the solvers used. These hierarchies can then be translated into shared and distributed memory mechanisms.
Of course, the hybrid model also combines the pitfalls of both shared memory and distributed computing, and ends up being much more complex. However, the final outcome is worth the effort! COMSOL Multiphysics provides sophisticated data structures and algorithms that represent and exploit multi-level parallelism to a large extent. It supports shared memory and distributed memory at the same time and the user can tune the interaction of both by a set of parameters for best performance.
Benchmarking Your Models and Your System
After all these theoretical explanations, it’s now time to connect the concept with real models. I suppose you are quite curious to investigate the scalability, the speedups, and the productivity gains when running COMSOL Multiphysics in parallel on the compute servers and clusters in your department.
In order to obtain proper results, it is very important to keep an eye on the problem size. The size of the subproblems on a shared memory node have to be large enough for every thread to obtain a reasonable amount of work and that the ratio of computations per process to the amount of data exchanged via messages between the processes is sufficiently large. As Pär had mentioned in his earlier blog post, it is crucial to consider whether problems are parallelizable at all. For example, if the major effort when setting up your model is dedicated to computing a long time-stepping series (that may last for hours) but the problem size in every time step is not significantly large, you will not see significant benefits when ramping up additional nodes and cores.
I encourage you to try various configurations of the hybrid model, even when you only have a shared-memory machine available.
A Hybrid Scalability Study
In the test scenario presented here, we consider a structural mechanics model representing a ten-spoke wheel rim where the tire pressure and the load distribution is simulated.

Model of a wheel rim and its corresponding submodel.
Our simulation is run on the three compute nodes mentioned above, where each node has two sockets with a quad-core Intel Xeon® E5-2609 processor with 64 GB RAM per node, and where 32 GB are associated with a processor. The nodes are interconnected by (a rather slow) Gigabit ethernet connection. In total, we have 24 cores available on this particular machine.
In the graph below, we compare the number of simulations of this one model that can be run per day, according to the hybrid model configuration. We consider the case of 1, 2, 3, 6, 12, and 24 MPI processes running. This leads to 1, 2, 3, 4, 6, 8, 12, 16, and 24 active cores running, depending on the configuration. Each bar in the graph represents an (nn x np)-configuration, where nn is the number of processes, np is the number of threads per process, and nn*np is the number of active cores. The bars are grouped into blocks with the same active core count, where their configuration is listed at the top of the bars.
The graph shows that the performance increases, in general, with the number of active cores. We see slight variations for the different configurations. When reaching the full system load with 24 active cores, we find that the best configuration is to assign one MPI process per socket (i.e. six MPI processes in total). The performance and productivity gain on the three-node system with a hybrid process-thread configuration (case 6×4) is more than twice as good as the performance on a single shared memory node (case 1×8). It is also almost 30% better than the completely distributed model (case 24×1), which uses the same number of cores.
When comparing this to its neighboring fully-distributed configuration (case 12×1), we see that there is no real gain in performance despite doubling the number of cores. This is because the slow Gigabit ethernet network is already very close to its limits with 12 MPI processes. More MPI processes are therefore not beneficial. The situation is different when comparing the 12×1- and 12×2-configurations, where the number of threads per process is doubled along with the number of active cores. This basically means that, in this case, the amount of communication via ethernet is not increased.
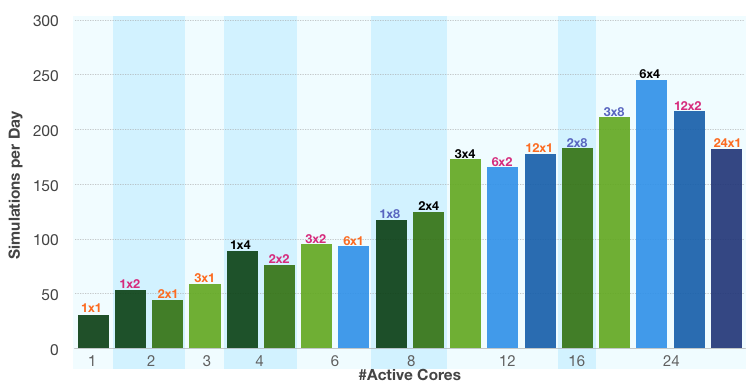
Benchmarking a structural mechanics model of a wheel rim using different configurations in a hybrid model. The y-axis indicates performance and productivity gain through the total number of simulations of this model that can be run during a day. The bars indicate different configurations of nn x np, where nn is the number of MPI processes, and np is the number of threads per process.
Setting up Hybrid Runs in COMSOL Multiphysics
When running COMSOL Multiphysics in the parallel hybrid mode, you have various possibilities to adjust the number of processes and threads used. Some settings can be found in the Multicore and Cluster Computing section in the Preference dialogue or in the Cluster Computing subnode of the Study node in the Model Builder. You can fine-tune the settings in the Cluster Computing subnode of the Job Configurations node, where you can specify the number of (physical) nodes you want to use in your cluster computation. Using the drop-down menu in the Settings window, you have additional choices, like the number of processes per host or the node granularity, which decides whether to put one process per node, socket, or core.
The number of threads used per process is set automatically. COMSOL Multiphysics always utilizes the maximum number of available cores, i.e. the number of cores per process is set to the number of available cores on the node divided by the number of processes on the node. You can override the number of cores per process by setting the Number of processors in the Multicore section of the Preferences dialogue to the requested value.
On Linux systems, you have the command line options -nn for the number of processes, -np for overwriting the automatically determined number of threads per process, and the option -nnhost that sets the number of processes per host. A natural choice for nnhost is either 1 or the number of sockets per node.
Next Steps
- For additional options, use cases, and examples please refer to the COMSOL Multiphysics documentation.
- Our final post in this Hybrid Modeling blog series will be on the topic of batch sweeps.



Comments (1)
Gavin
March 27, 2015Could you also comment on the -numasets flag please?