Elements of Chemical Reaction Engineering: COMSOL Models
The textbook Elements of Chemical Reaction Engineering by H. Scott Fogler provides a complete overview of the principles of chemical reaction engineering in a structure that enables students to solve problems through reasoning rather than memorization. The fourth edition of the book focuses on bioreaction engineering and industrial chemistry and includes a wide variety of industry applications.
The textbook features model examples that have been formulated and solved using the COMSOL Multiphysics® software. Each problem is described and summarized in the documentation, which also includes step-by-step instructions to reproduce the corresponding models and derive the model equations in detail.
In order to reproduce these COMSOL models, a valid COMSOL Multiphysics license is required. The license allows you to run the models featured on this page. In some cases, the Chemical Reaction Engineering Module license may also be required. Check with your teacher or teaching assistant to see if such licenses are available on your campus computer system.
There are five different COMSOL Multiphysics model examples included in Elements of Chemical Reaction Engineering. We will first summarize these examples and then explore them in greater detail below.
COMSOL Model Summaries
Tubular Reactor
The Tubular Reactor model investigates how radial variations in composition and temperature affect the performance and operation of tubular reactors. This exercise contains four separate submodels:
- Isothermal reactor
- Nonisothermal adiabatic reactor
- Nonisothermal reactor with isothermal cooling jacket
- Nonisothermal reactor with nonisothermal cooling jacket
An axisymmetric tubular reactor, modeled in the first exercise.
One-Dimensional Tubular Reactor
The One-Dimensional Tubular Reactor model analyzes the formulation of different boundary conditions, the purpose of using dimensionless numbers, and how the value of these dimensionless numbers characterizes the dispersion and reaction distribution in plug flow reactors. We can see the formulation of the model equations in a dimensionless form in terms of the Péclet and Damköhler numbers. The problem is defined with two different types of boundary conditions:
- Formulation with Danckwerts boundary conditions
- Formulation with upstream and downstream sections, where dispersion occurs but no reactions
A plug flow reactor, modeled with Danckwerts boundary condition (top) and inlet and outlet sections (bottom).
Nonisothermal Plug Flow Reactor
The Nonisothermal Plug Flow Reactor model shows how to use thermodynamics from the JANAF and NASA polynomials. The modeled system is a reactor for the production of acetic anhydride. The model includes a detailed description of its thermodynamic and kinetic properties, in contrast to the Tubular Reactor model, which uses the approximation of the constant heat transfer coefficient and heat capacity. Two cases are investigated:
- Adiabatic nonisothermal reactor
- Nonisothermal reactor with heat exchange
Two plug flow reactor model studies: Nonisothermal adiabatic (top) and nonisothermal with heat exchange (bottom).
Determination of Arrhenius Parameters
Determination of Arrhenius Parameters defines a model for a perfectly mixed batch reactor, typically for laboratory scale experiments where reaction kinetic data is measured. The data from the experiments is used for parameter estimation for the parameters in the model equation. The exercise demonstrates a typical use of modeling and simulation to extract kinetic data from experiments.
A lab-scale reactor allows for excellent control of the composition of temperature, which is required for parameter estimation.
Startup of a Continuous Stirred Tank Reactor (CSTR)
Startup of a Continuous Stirred Tank Reactor (CSTR) models a nonideal CSTR using a set of two CSTRs. The startup of CSTRs is a classic example of how to use simulation to investigate safe operating conditions.
The startup of a nonideal CSTR is simulated using two coupled ideal CSTRs: CSTR1 and CSTR2. The results show the concentration (y-axis) as a function of temperature (x-axis) over time for different initial conditions. The graph shows how the three different starting conditions give the same final steady-state temperature and concentration at the outlet, at about 450 mol/m3 and 337 K, where the three curves meet.
Detailed Model Explanations
1. Tubular Reactor
The Tubular Reactor model is the most comprehensive modeling and simulation exercise for tubular reactors. It includes radial and axial variations in the fluid flow velocity, composition, and temperature. The purpose of the exercise is to understand how radial variations in composition and temperature are influenced by the presence of a cooling jacket, which may be used to control the performance of a tubular reactor. The exercise also shows how the properties of the reactions and the reactor may influence the performance.
Problem Definition
The process described in the exercise is for the exothermic reaction of propylene oxide with water to form propylene glycol.
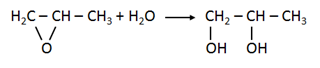
This reaction takes place in a tubular reactor equipped with a cooling jacket in order to avoid explosion.
The reaction kinetics is first order in regard to the concentration of propylene oxide, assuming that water is available to such a large excess that its concentration is constant. Further, assuming identical transport properties for the propylene oxide and propylene glycol and that these species are present in a dilute water solution makes it possible to approximate the concentration of propylene glycol from the concentration of propylene oxide and the stoichiometry of the reaction.
The model equations describe the conservation of material and energy. The dependent variables are the concentration and the temperature in the reactor. A third dependent variable describes the temperature in the cooling jacket along the length of the reactor. The flow in the cooling jacket is turbulent, which implies that plug flow with negligible variations in temperature along the radius of the cooling jacket is a decent assumption.
The material and energy equations in the reactor are defined along two independent variables: the radial and axial directions. These equations form a system of two coupled partial differential equations (PDEs) along the radius and length of the reactor. The velocity field in the reactor is described by the Hagen-Poiseuille equation for fully developed laminar flow. This is described by a parabolic expression with respect to the radius.
Only a 2D cross section (light blue) of the reactor needs to be modeled due to axial symmetry. The composition and temperature vary in the r and z directions. The cooling jacket temperature only varies in the z direction at the position r = R.
Operating Conditions and Parameter Study
From isothermal conditions to including the energy balance in the cooling jacket, the complexity of the reactor model increases in the following steps in the exercise:
- Isothermal reactor
- Nonisothermal adiabatic reactor
- Nonisothermal reactor with isothermal cooling jacket
- Nonisothermal reactor with nonisothermal cooling jacket
The parameters that can be varied for the operating conditions above are the following:
- Thermal conductivity in the reactor
- Heat of reaction (enthalpy of reaction)
- Activation energy
- Average inlet velocity in the reactor
Tubular Reactor Exercise Downloads
Download the latest versions of the COMSOL Multiphysics files for the application and the embedded model:
2. One-Dimensional Tubular Reactor
The velocity profile in tubular reactors, in the presence of a porous catalyst or for turbulent flow, can often be approximated with a uniform constant value as a function of the reactor radius, i.e., the profile of a plug flow. In such cases, the material and energy balances are only dependent on the axial direction and time, which yield one-dimensional differential equations as model equations.
The material balances for such a 1D model can be solved by adding inlet zones before and after the reactor. In these zones, the concentration profiles in the direction of the flow are no longer important, since the reactions are not present to create them. As an alternative, Dankwertz conditions can be used instead of these zones. This example compares these two strategies for setting boundary conditions. In addition, the example also uses dimensionless equations, which can be characterized by the dimensionless Péclet and Damköhler numbers.
Problem Definition
The material balance along the length of the reactor is at steady state for a flat velocity profile. A first-order irreversible reaction is formulated as follows:
\frac{d}{{dx}}\left( { - D\frac{{dc}}{{dx}} + cU} \right) + kc = 0
(1)
where D denotes the dispersion coefficient, U is the flow velocity, k is the rate constant for the reaction, and c is the reactant (or product) concentration.
We may introduce the following dimensionless variables in order to generalize the material balance above for any reactor length, L; inlet concentration, c0; and flow velocity:
C = \frac{c}{{{c_0}}} \enspace \mathop \to \limits^{yields} \enspace dc = {c_0}dC; \enspace X = \frac{x}{L} \enspace \mathop \to \limits^{yields} \enspace dx = LdX
(2)
Combining the expressions above with the material balance results in:
\frac{d}{{dX}}\left( { - \frac{{D{c_0}}}{{{L^2}}}\frac{{dC}}{{dX}} + \frac{{{c_0}}}{L}CU} \right) + k{c_0}C = 0
(3)
Multiplying the expression above by \[\frac{L}{{U{c_0}}}\] yields:
\frac{d}{{dX}}\left( { - \frac{D}{{UL}}\frac{{dC}}{{dX}} + C} \right) + \frac{{kL}}{U}C = 0
(4)
We can now introduce the Péclet number (Pe) and the Damköhler number (Da):
Pe = \frac{{UL}}{D}; \enspace Da = \frac{{kL}}{U}
(5)
The material balance, for a constant dispersion coefficient, can then be written according to the following:
- \frac{1}{{Pe}}\frac{{{d^2}C}}{{d{X^2}}} + \frac{{dC}}{{dX}} + DaC = 0
(6)
The Péclet number relates the convective transport of a species with its transport by dispersion. The larger the convection, the larger the Péclet number becomes. The Damköhler number relates the reaction term with the dispersion. When the reaction term increases, the Damköhler number also increases.
The equation above can be solved with the proper boundary conditions. The Danckwertz condition sets the flux at the inlet according to the following expression:
- \frac{1}{{Pe}}\frac{{dC}}{{dX}} + C = {C_0} \enspace at \thinspace X = 0
(7)
where C0 is a constant dimensionless concentration.
Note that the expression on the left-hand side of the equation above is the dimensionless flux of the modeled species. The first term is the dimensionless dispersion and the second term is the dimensionless convective contribution. The dimensionless flux is set equal to the dimensionless convective flux of a concentration C0. At the outlet, the flux is instead set to:
\frac{1}{{Pe}}\frac{{dC}}{{dX}} + C = C \enspace at \thinspace X = 1
(8)
which effectively sets the dispersion term to zero at the outlet, since the convective terms on the left- and right-hand side convect the same concentration value, C, at the outlet.
As an alternative to the two boundary conditions, we can add the inlet and outlet zones mentioned above and then set the conditions at the inlet and outlet to these zones:
C = {C_0} \enspace at \thinspace X = 0 - \frac{{{L_{inlet \thinspace zone}}}}{L}
and
\frac{1}{{Pe}}\frac{{dC}}{{dX}} + C = C \enspace at \thinspace X = 1 + \frac{{{L_{outlet \thinspace zone}}}}{L}
(9)
The last condition also sets the dispersion term equal to zero, but far from the outlet, which would allow for a dispersion contribution to the flux at the true position of the outlet. The figure below shows the assumption for the two cases above.
Influence of Boundary and Operating Conditions
The operating conditions can be varied by changing the Péclet and Damköhler numbers:
- Péclet number over a range from x to y
- Damköhler number over a range from x to y
The variations can be run for the two cases above, with and without inlet and outlet zones.
The two sets of boundary conditions with inlet and outlet sections (bottom) and without inlet and outlet sections (top).
One-Dimensional Tubular Reactor Exercise Downloads
Find the latest version of the COMSOL Multiphysics files for the application and the embedded model at the link below:
3. Nonisothermal Plug Flow Reactor
This example considers the thermal cracking of acetone, which is a key step in the production of acetic anhydride. The gas phase reaction takes place under nonisothermal conditions in a plug flow reactor. As the cracking chemistry is endothermic, control over the temperature in the reactor is essential in order to achieve reasonable conversion.
The thermal cracking of acetone to ketene and methane is described by the following equation:
\[C{H_3}COC{H_3} = C{H_2}CO + C{H_4}\]
(10)
The reaction rate is given by an irreversible first-order reaction with respect to the concentration of acetone.
In the first case, the reactor is assumed to be insulated at the walls; i.e., everywhere except at the inlet and outlet. In the second case, a heater is included, which accelerates the endothermic reaction above. The two cases are illustrated in the figure below.
The two cases studied in this exercise, with and without heat exchange.
Problem Definition
The model equation at steady state for the material balance of a reacting species in a plug flow reactor for a first-order reaction is introduced in the exercise above. According to the following equation:
\frac{d}{{dx}}\left( { - D\frac{{dc}}{{dx}} + cU} \right) + kc = 0
(11)
In this equation, c denotes the species concentration, D is the diffusion coefficient, and k is the rate constant for the reaction. One material balance is required per chemical species. Note that the reaction rate only depends on the acetone concentration.
The boundary conditions are Danckwertz conditions:
- D\frac{{dc}}{{dx}} + cU = {c_0}U\enspace at \thinspace x = 0
(12)
where c0 is the concentration of the inlet stream, upstream from the inlet. At the outlet, we have:
- D\frac{{dc}}{{dx}} + cU = cU \enspace at \thinspace x = L
(13)
where L denotes the length of the reactor.
For the thermal balance, we have a similar equation:
\frac{d}{{dx}}\left( { - \kappa \frac{{dT}}{{dx}} + T\rho {C_p}U} \right) + kc\Delta H - {q_{ext}} = 0
(14)
In the above equation, T denotes temperature, k is the thermal conductivity, Cp is the heat capacity, r is density, qext is an external heat source per unit volume, and DH is the heat of reaction.
Also, the boundary conditions for the thermal balance are of the Danckwertz type:
- \kappa \frac{{dT}}{{dx}} + T\rho {C_p}U = {T_0}\rho {C_p}U \enspace at \thinspace x = 0
(15)
where T0 is the temperature upstream from the reactor. At the outlet, we have
- \kappa \frac{{dT}}{{dx}} + T\rho {C_p}U = T\rho {C_p}U \enspace at \thinspace x = L
(16)
The complication here is that the properties in the gas phase in this model are not constant. The heat capacity, density, and heat of reaction all depend on the composition. For each of the involved species, and assuming an ideal gas mixture, the properties are obtained from the NASA polynomials for thermodynamic properties.
Influence of Heating
The problem above is solved for these two cases:
- Adiabatic: qex = 0
- External heating: qex = qex,0
Nonisothermal Plug Flow Reactor Exercise Downloads
Try it yourself. Download the latest version of the COMSOL Multiphysics files for the application and the embedded model used in this exercise:
4. Determination of Arrhenius Parameters
This example shows how to use reactor modeling in combination with parameter estimation in order to find the Arrhenius parameters of a first-order reversible reaction. The same approach can be used for irreversible second-order reactions.
Problem Definition
This model studies the gas phase reaction of the decomposition of benzene diazonium chloride to benzene chloride:
The rate expression for the irreversible reaction is the following:
{r} = {k}{c_{Ph{N_2}Cl}}
(17)
where the rate constant is given by the Arrhenius equation according to:
k = A \cdot {e^{\left( { - \frac{{{E_A}}}{{RT}}} \right)}}
(18)
The Arrhenius parameters, A and Ea, may be obtained by parameter estimation using data from a set of experiments in a perfectly mixed isothermal batch system with constant volume. The concentration of benzene diazonium chloride as a function of time can then be used as an objective function for the temperatures: 313 K, 319 K, 323 K, 328 K, and 333 K.
Parameter Estimation
The parameter estimation solver is more efficient in finding an optimal parameter set if the model experiences similar sensitivity with respect to changes in parameter values.
In this problem, a parameter, Aex, is defined to be estimated together with the activation energy, Ea, such that the rate constant is written as:
k = {e^{{A_{\operatorname{ex} }}}} \cdot {e^{\left( { - \frac{{{E_A}}}{{RT}}} \right)}}
(19)
Determination of Arrhenius Parameters Exercise Downloads
Check out the COMSOL Multiphysics files for the application and the embedded model in this exercise:
5. Startup of a Continuous Stirred Tank Reactor (CSTR)
In this model example, we investigate the startup phase of a continuous stirred tank reactor (CSTR) used to produce propylene glycol. The nonisothermal process is described by a set of coupled mass and energy balances. The model highlights the use of the predefined CSTR reactor type and also shows how to enter thermodynamic data needed for the energy balances. Results show how certain initial conditions lead to the violation of reactor safety limits.
Problem Definition
Propylene glycol (PrOH) is produced from the reaction of propylene oxide (PrO) with water (H2O) in the presence of an acid catalyst:
The reaction rate is given by the following first-order expression with respect to propylene oxide:
r = k{c_{\Pr O}}
(20)
where the rate constant is given by the usual Arrhenius equation:
k = {e^{{A_{\operatorname{ex} }}}} \cdot {e^{\left( { - \frac{{{E_A}}}{{RT}}} \right)}}
(21)
The figure below shows the notations used in the model of one CSTR.
Here, Vr denotes the reactor volume, vf is the flow rate of the feed, Tf is the temperature of the feed, and cf,i is the concentration of species i in the feed. The variable v is the outlet flow rate, T is the temperature in the reactor and outlet stream, and ci is the concentration of species in the reactor and outlet stream. The material balance for one tank is given by the following equation:
Notations used in the model equations for one CSTR.
{V_r}\frac{{d{c_i}}}{{dt}} = {v_f}{c_{i,f}} - v{c_i} + r{V_r}
(22)
{V_r}\sum {{c_i}{C_p}\frac{{dT}}{{dt}}} = \sum {{h_{i,f}}{v_f}{c_{i,f}} - \sum {{h_i}v{c_i}} } - \Delta H \cdot r{V_r} + {Q_{ext}}
(23)
where Qext denotes the added heat through the heating system and hi is the enthalpy of species i.
We can then connect two CSTRs according to the figure below in order to model a nonideally mixed CSTR.
This also means that we have two sets of equations for the material and energy balances, one for each CSTR. The two CSTRs are coupled through the outlets and inlets between the reactors.
Two connected CSTRs may represent one nonideally mixed CSTR.
Operating Conditions
The reactor is simulated for three different initial conditions:
- T = 295 K, and cPrO = 0 mol/m3
- T = 340 K, and cPrO = 0 mol/m3
- T = 340 K, and cPrO = 1400 mol/m3
The aim of the exercise is to find out if the starting conditions may lead to a violation of the safety limits for the operating conditions during the startup cycle.
Startup of Continuous Stirred Tank Reactor Exercise and Related Downloads
Download the latest versions of the COMSOL Multiphysics files for the application and the embedded model:
- Startup of Continuous Tank Reactor
- Parameter Estimation for Nonideal Reactor Models
- Ideal Stirred Tank Reactor System