|
| Filename | Size |
|---|---|
| README.txt | 2 KB |
| Download all files (Zip-archive) | ~ 1 KB |
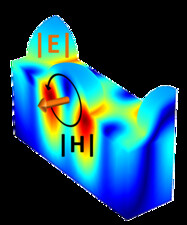
multipole decomposition of dielectric nanoparticles in an array
Juan Luis Garcia, CSIC
These files of COMSOL and MATLAB make the calculation of the electromagnetic fields for a hexagonal array of Silicon hemispheres over a dielectric (mesoporous titania) array of cylinders with the same arrangement over a base layer of the dielectric on top a silica substrate.
The multipole decomposition of the particles is made and the surface energy and reflectance are calculated.
If you use this files, please, cite as
Molet, P., Gil-Herrera, L., Garcia-Pomar, J., Caselli, N., Blanco, Á., López, C., & Mihi, A. (2020).
Large area metasurfaces made with spherical silicon resonators, Nanophotonics, 9(4), 943-951.
doi: https://doi.org/10.1515/nanoph-2020-0035
Steps
1.Download the files from https://zenodo.org/record/4009029#.X00FljXtZhE (exceed the limit here)
2. Create a folder called C:\datacomsol\
3. Change the geometric and materials parameters if you want.
4. Run the COMSOL files (v.5.5) (_RF for Radiofrequency module or _WO for Wave optics module).
5. Clear all the tables in Tables.
6. Evaluate all the derived values.
7. Export all the data in Export.
8. run Matlab file (v.2010b).
User Comments
|
Jan 31, 2023 at 3:58pm UTC |
|
As far as I understand, you use equations for multipole decomposition of SCATTERED LIGHT by A SINGLE ISOLATED PARTICLE, and apply these formulas for particles in a n array, which seems to be incorrect from the beginning. |
|
Entry submitter Oct 25, 2023 at 12:30pm UTC |
|
You can apply this method for metasurfaces due the interaction between particles is included in the internal fields. |
Login to comment on this entry.
