FE-Simulation of PTCA Balloon Catheters
Within 40 years, percutaneous transluminal coronary angioplasty (PTCA) catheters evolved into the golden standard for treating coronary stenoses. However, navigating through tortuous vessel pathways and cracking highly calcified lesions is challenging. To minimize the risk of complications, catheters require special properties. Due to the high safety requirements and the design complexity, the development and optimization of catheters is a challenging and costly procedure. To reduce the prototype costs, Finite Element (FE) Simulations may assist the development process, in order to increase device safety, while reducing the costs. The scheme of a catheter is shown in Figure 1.
Use of COMSOL software in this project Different simulations have been used to aid the design process of a PTCA Balloon catheter: - 2D Simulation of different two-lumen distal shaft geometries to optimize the geometry regarding burst-pressure and inflation time - 3D Simulation of superposition of different load cases (e.g. bending and pressure) - 2D/3D Simulation of the folding process of a balloon
Material Model (see figure 2) A large strain elastoplastic material model, with von Mises yield function and user-defined hardening curve, is used in the Nonlinear Structural Material Module. The true-stress is given as a function of the true-strain by using an interpolation function (int1). The user-defined hardening function is defined by the following equation using the Young’s Modulus (solid.E) the von Mises Stress (solid.mises), the initial yield stress (solid.sigmags) and the effective plastic strain (solid.epe). max(0, int1(solid.epe+solid.mises/solid.E)-solid.sigmags).
2D Simulation: Shaft Design The outer diameter of the shaft (see figure 3) has a fixed constraint at one point (red) and a prescribed displacement, which only allows the expansion normal to the blue point. The inner surface is pressurized with 3 MPa. In a real case scenario, a superposition of different load cases (e.g. bending and pressure) is expected. Therefore, a 3D 3-Point-bending test is simulated. Between a circular indenter, the shaft, and two circular supports, frictionless contacts are defined. To prevent rigid body motion at the beginning of the simulation a spring foundation (k(1-RampFactor)2^(-10*RampFactor)) is applied to both ends of the shaft. The RampFactor increases from 0 to 1 during the static simulation.
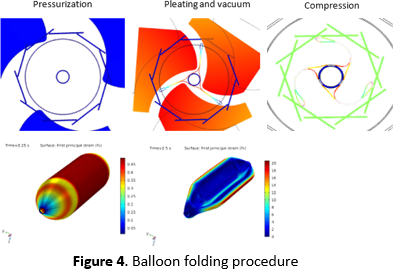
2D and 3D FE models of the folding of the Balloon: To reduce the cross-section of the balloon, it is usually folded in a four-step process: Pressurization, pleating, vacuum, and compression (see figure 4). The dies for the pleating and the compression are simulated as rigid domains with a prescribed rotation in a quasi-static time-dependent analysis. Between the dies and the balloon frictionless contacts are defined.
Summary The design of a suitable and innovative shaft geometry can be aided using FE-Simulations and unnecessary costs for trial and error prototypes are being avoided. Pleated balloons improve the prediction of stent expansion and the interaction between the balloon and the artery. Furthermore, a simulation with the folded balloon in combination with the arterialwallmechanics module from the application library is planned, in order to observe the influence of the balloon folding and wall thickness onto the balloon expansion properties inside coronary arteries.