Linking The Dimensions
Published in 2011
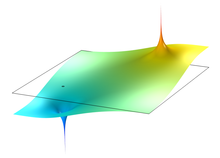
We consider a 3D boundary value problem arising in electrostatics. The potential is stimulated by current sources placed on a cross-section S of the domain. In many applications it is sufficient to know the potential in S. So, one is interested in an appropriate 2D model taking into account that the solution depends on the dimension of the domain.
The idea is to find a corresponding 2D boundary value problem, such that its solution coincides with the 3D solution restricted on S. This can be done approximatively by means of a correction term in the partial differential equation. The method speeds up the direct problem solver and especially can be utilized to improve the performance of the electrical impedance tomography.
Download
- helfrichschkarbanenko_paper.pdf - 0.14MB
