Modeling Approach to Facilitate Thermal Energy Management with Phase Change Materials (PCM)
Thermal energy storage systems receive notable attention within the framework of energy management due to their ability of bridging thermal energy demand and supply, thus leading to an overall efficiency increase. The key component in such systems are materials which convert extraordinarily large amounts of heat during solidification and melting processes. These materials are labeled as phase change materials (PCM).
Latent heat storage systems profit from the PCM’s ability to capture or release heat at a constant temperature while the phase change occurs. Due to the large selection of PCM with different specifications and application purporses an intelligent selection is a challenging task. To reduce design and development costs of PCM-based applications a numerical model proves to be a powerful tool.
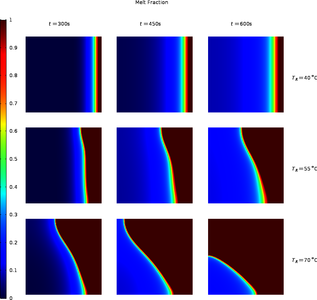
The modeling approach in this work is conceived by means of a test-case on a simple 0.01x0.01 m2 2D square geometry with variable boundary heating on the right side while all other walls are adiabatic. The chosen PCM in this test-case is the paraffin wax n-eicosane which has an extensive experimental coverage. Due to remarkable influence of natural convection the model considers both fluid dynamics and heat transfer in a fully coupled transient study. The phase change characteristic is introduced by a set of customized equations for thermal properties such as melted fraction θ, modified heat capacity Cp, modified thermal conductivity k and density ρ around the modeling parameter ΔT which creates a so-called “mushy zone” where liquid and solid coexist as a porous media.
The model is set up with the basic COMSOL Multiphysics® module which includes the required laminar flow interface and heat transfer in fluids interface. The customized equations accounting for the phase change process are implemented with analytical functions into additional source terms of the incompressible momentum equations to distinguish between liquid fraction and solid fraction. Within the liquid fraction the velocity field is accelerated by the arising volume force of a naturally convecting fluid due to temperature differences (Boussinesq approximation). Due to the sharp increase of viscosity (up to 10E8 Pa*s) of the solid phase the momentum equation can conveniently be solved on the entire domain while a flow field is induced in the liquid phase only.
The physical model description has been further developed in order to include a thermal hysteresis for testing PCM where melting and freezing point do not coincide. The modeling approach in 1D allows for a strategic and goal-oriented investigation of appropriate PCM types. A practical application example is given by means of a wall cross-section of a wooden cabin and a commercially available PCM mat for building purposes. The PCM layer in the insulation of the wall absorbs heat during peak temperatures of the day and releases heat during the night. The example illustrates how the PCM layer damps the temperature oscillations from outside and from internal heat loads while maintaining thermal comfort indoors without the need of energy-intensive cooling or heating equipment.
Download
- rubinetti_presentation.pdf - 2.2MB
- rubinetti_paper.pdf - 0.39MB
- rubinetti_abstract.pdf - 0.1MB



