Simulating Wear in Disc Brakes
Wear is a complex phenomenon relevant to many problems involving frictional contact, such as mechanical brakes, seals, metal forming, and orthopedic implants. The rate of wear depends on the properties of the contacting materials and operating conditions. One widely used model of wear is Archard’s law, which relates the rate of material removal due to wear to the contact pressure, sliding velocity and a material parameter. A generalized version of Archard’s law exists that includes the effect of temperature. We have implemented such a wear law as a boundary ordinary differential equation (ODE) in a COMSOL Multiphysics® simulation with the wear depth/thickness as the independent variable. The wear ODE is solved on the faces of the brake pads in contact with the rotor and the wear depth was used to modify the distance between the contacting surfaces in the contact formulation. This approach avoids altering the model geometry to account for material loss due to wear, and only marginally increases solution time and model size. The approach is only suitable for cases in which the amount of wear is significantly less than the width of the contact surfaces.
We illustrate the new contact-offset based wear model implementation by simulating wear in automotive disc brakes. We developed a 3D thermal-structural disc brake model involving representative brake disc/rotor and brake pads (Figure 1). The structural and thermal problems are coupled through frictional heat generation, thermal expansion, and thermal contact. Both fields are coupled to the wear evolution equation. The rotation of the brake rotor was not explicitly modeled in the structural deformation. We accounted for rotation in the thermal field by applying a rotational convective term in the heat transfer equation. We also accounted for brake rotation in the calculation of frictional forces and frictional heat generation. We used a fully coupled direct solver to handle the strong coupling between the three physical fields. We applied a pressure load to the back plate of the brake pads to put them in contact with the rotor.
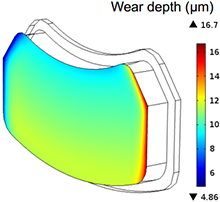
The wear evolution is not uniform along the surface of the lining due to the non-uniform initial contact pressure profile and the non-uniform sliding velocity. Figure 2 shows contact pressure profiles at the onset of contact and after 100 seconds for one set of loading conditions, where we did not account for thermal expansion. Initially, highly localized stresses exist at the leading edge of the brake lining due to friction. After 100 seconds, a smoother contact pressure profile exists due to wear. Figure 3 shows the wear thickness profile at 100 seconds for the same simulation. We will also show the evolution of wear thickness and contact pressure profiles for other cases involving thermal effects.
Download
- elabbasi_presentation.pdf - 0.9MB
- elabbasi_abstract.pdf - 0.34MB
