Simulation of a Vortex Ring: Dealing with the Unbounded, Doubly Connected Domain
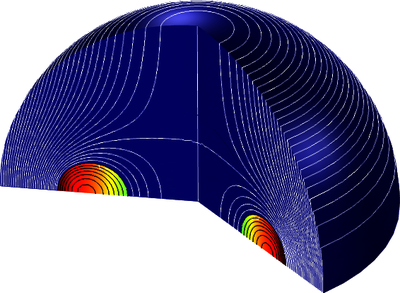
This talk is for intermediate-level users of COMSOL who, like the present author, are relative newcomers to numerical simulation but have a strong grounding in Hydrodynamics or related areas of Mathematical Physics. Most turn-key Computational Fluid Dynamics packages, including COMSOL’s, are well suited to the simulation of internal flows where the user has in mind a definite inlet, outlet, and sidewalls---so the domain occupied by the fluid is bounded, by definition. By contrast, user’s interested in external flows, e.g. in Aerodynamics, must deal with unbounded domains. The Vortex Ring furnishes an example of a relatively simple flow, which nevertheless, presents the challenges of an unbounded doubly-connected domain with a bounded subregion region with nonzero vorticity (i.e. fluid spin). The present work describes a simulation constructed with tools from COMSOL Multiphysics alone, i.e. without any add-on modules. The only Physics Interfaces it employs are of the General Form PDE type. The vortex core is interior to a torus of circular meridional section. One may then draw a sphere---hereinafter called the reflecting sphere---centered at the center of the torus and of radius ‘a’ large enough to contain all parts of the torus. There are then three computational domains, namely: (i), the interior of the torus (i.e. the core); (ii), the region between the torus and the reflecting sphere; and (iii), the exterior of the reflecting sphere. One may introduce a change of independent variable---so-called Kelvin Inversion---that maps the exterior of the reflecting sphere---which I will call the exterior physical domain---to the interior of another sphere, also of radius ‘a’, which I will call the proxy domain and denote by Roman numeral (iv). In short, one may build a single root model in COMSOL with three Components that calculate the Stokes stream function, psi, in Domain (i); the velocity potential, Phi, in Domain (ii); and the velocity potential, Phi, in Domain (iv) with Model Coupling Operators (of General Extrusion type) to relate the local boundary fluxes. To generate a circulatory solution in Domain (ii) one must cut that domain to make it simply connected by introducing a diaphragm in the equatorial plane of the torus bounded by its inner equator. COMSOL allows a jump in Phi across the diaphragm through the use of a Boundary Similarity model coupling. One then simulates a propagating vortex ring as a linear combination of three elementary solutions, namely: a rotational solution in the core, an irrotational solution with circulation and no remote free stream, and an irrotational solution with a remote free stream and no circulation. The combination must satisfy compatibility of circulation between the concave and convex sides of the torus and no slip across it.
Download
- russell_presentation.pdf - 0.6MB
- russell_paper.pdf - 1.44MB
- russell_abstract.pdf - 0.07MB
