Structural Mechanics, Acoustics Module - Numerical Study of Loudspeaker Diaphragm Geometry
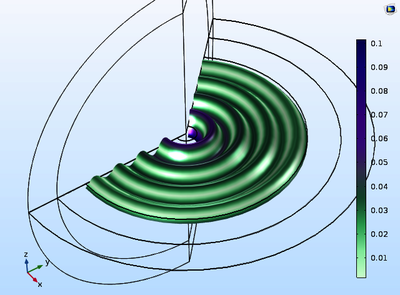
The study of loudspeaker diaphragm geometry is aimed to focus on how does the distribution of mass in the radial direction changes the ‘dynamic and acoustic response’ of the diaphragm. The geometry is subjected to concentrating the mass by changing the shape of our interest in a 2D rectangular geometry in COMSOL Multiphysics®, while the total volume is kept as constant (Total mass is constant). Since the total volume is kept as constant, it is easy to control the shape of the plate by splitting it into segments and possibly inferred as thickness variation in the x-axis of the 2D model and in the radial direction in an axisymmetric model. This study signifies the importance of the ‘Eigen frequency pattern’ changes versus position of the concentrated mass. This study extends from a 2D plate model to 2D circular plate and cone-shaped plate diaphragm.
The model is initially studied for the dynamic responses by establishing the solid mechanic's module and later subject to the acoustics module interface to study the acoustic response. A very simply 2D plate model with 2D and 2D-Axisymmetrical geometries makes the study viable and keeps the research aspects interesting and clear. The motivation of keeping the mass constant while the 2D plate model is subjected to the different mass distributions is to understand the dynamic responses in better and easy way. Another interesting aspect could be 2D shape change influences the acoustic response also radiation aspects of the plate. And the Initial results of 2D (Rectangular) plate are verified by the analytical method.
2D (Rectangular), 2D-Axisymmetric (Circular) plate models were implemented using COMSOL 2D Geometry Operations and controlling this geometry is performed by controlling the volume. For a 2D (Rectangular) plate this operation is straight and easy while 2D-Axisymmetric (Circular) case the volume is subjected to polar coordinates, where Integral calculus is applied with control variables to control the geometry in COMSOL. Achieving the constant mass for every for every different position of concentrated mass is key for the study.
Maintaining the total volume to be constant leads to the importance of keeping the mass constant for the modal analysis and thus enables the study of geometry modification and its influence on modes and mode shapes. It was also our interest not to increase the mass since that directly influences the sensitivity of the driver and this is not the interest of the study.
The computations performed in this analysis will be studying the modes and mode shapes and how does the modes increases or drops with geometry modifications. It would be further extended with the interest of controlling a geometry with the specific interest of frequency contents. This study is currently on the conical shape plate model with distributed mass and the result will be subjected to deep comprehension.
Download
- mageswaran_poster.pdf - 0.59MB
- mageswaran_paper.pdf - 0.66MB
- mageswaran_abstract.pdf - 0.03MB
