The Numerical Challenges in Multiphysical Modeling of Laser Welding with ALE
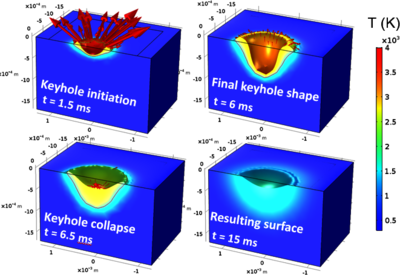
The interaction of high power laser beam with metallic materials produces a number of interconnected phenomena that represent a serious challenge for numerical modeling, especially for creation of auto-consistent models. Additional difficulty consists in lack of data on materials properties at the temperatures superior to their melting point. The present work summarizes the numerical challenges in creation and validation of free-surface models using ALE moving mesh coupled with heat transfer equation and Navier-Stokes fluid flow. The performances of different formulations of ALE method are compared : Lapace, hyperelastic, Winslow and Yeoh. The influence of a set of numerical parameters (inconsistent stabilization, fictive viscosity of solid, mesh quality etc), as well as physical hypotheses (the variation of adsorption coefficient and liquid viscosity with temperature etc) on the dynamics of the keyhole and the characteristics of the melt formed in titanium alloy Ti-6Al-4V is analyzed. Amongst different formulations of ALE method, hyperelastic deformation gives the better results for keyhole digging problem. The main limitation of keyhole digging from the numerical point of view is determined by the rapid increase of mesh distortion (>2.5), which leads to the inaccurate solving of the keyhole bottom followed by calculation error. This problem can be treated with different remesing approaches that increase the time of calculation to the high degree. Another big numerical problem is the parasite velocity field in the part of material considered to remain solid. Insufficient value of fictive viscosity makes important influence on temperature evolution and fluid dynamics, as well as produces unphysical relaxation of solidified matter in the ring around the zone of impact. Too high fictive viscosity, however, leads to the convergence problems. Gradual decrease of fictive viscosity with temperature can be used to stabilize the solution. Finally, the mass conservation during the keyhole progression and collapse was analyzed. The use of incompressible Navier-Stokes equation produced important loss of mass. Weakly compressible Navier-Stokes equation offers excellent mass conservation, however, the convergence of the models is more difficult due to higher temperature and velocity gradients and more rapid deterioration of element quality.
Download
- tomashchuk_poster.pdf - 1.01MB
- tomashchuk_paper.pdf - 0.76MB
- tomashchuk_abstract.pdf - 0.1MB
