Time Domain Analysis of Dielectric Relaxation
When a material is subjected to a sudden change in electric field, the polarization of the material takes a finite time to respond – this phenomenon is referred to as dielectric relaxation. Dielectric relaxation is critical to understanding the important analytic technique of impedance spectroscopy [1], which is widely applied to understand pure materials, composites [2] and more complex systems, including biological cells and tissues [3]. In the context of the study of insulating materials, impedance spectroscopy is sometimes referred to as dielectric relaxation spectroscopy.
The impedance of a material can be represented as a complex dielectric permittivity, and this is frequently the most convenient representation when simulating insulating materials. Frequently, such materials are characterized by multiple relaxation processes, each with a different timescale. In such a case, the complex permittivity of the material can be written in the form:
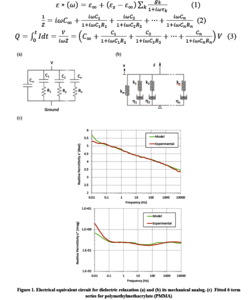
(1) Reference Figure 1, Eq. 1
where is the high frequency permittivity value, is the low frequency value, is the angular frequency and is the relaxation time for the th process. The relative contributions of the different relaxation processes to the permittivity are related to the coefficients with the restriction which is implied by this equation form. The well-known Debye model retains only the first term in this series. To understand this system, consider the impedance of the electrical circuit illustrated in Figure 1a. The total impedance, Z, of the circuit can be written in the form:
(2) Reference Figure 1, Eq. 2
The charge accumulated on all the capacitors is given by:
(3) Reference Figure 1, Eq. 3
Comparing equation (3) to (1) shows that the circuit can be used as an analog of the permittivity response (1), in the time domain. An additional analog is worth highlighting. The circuit of Figure 1a has a mechanical analog, illustrated in Figure 1b. Such an arrangement of springs and dampers is equivalent to the Generalized Maxwell model employed in viscoelasticity to represent the Prony series frequency response of the material. Using COMSOL Multiphysics® simulation software's existing functionality for viscoelasticity as a template, we have implemented equivalent functionality to represent the dielectric relaxation of insulating polymers in the time domain. Additionally, we present example simulation results for the time domain response of a composite polymer system. Figure 1c shows the frequency response of the fit from Equation (1) developed as part of this work.
References
1. E. Barsoukov, J. R. Macdonald, Impedance Spectroscopy: Theory, Experiment, and Applications, John Wiley and Sons (2018)
2. R. C. Smith, J. K. Nelson, and L. S. Schadler, Electrical behavior of particle-filled polymer nanocomposites, in Physical Properties and Applications of Polymer Nanocomposites,Woodhead Publishing (2010)
3. M. Wolf, R. Gulich, P. Lunkenheimer and A. Loidl, Broadband dielectric spectroscopy on human blood, Biochimica et Biophysica Acta 1810(8), 727-740 (2011)
Download
- ransley_presentation.pdf - 0.85MB
