Modeling with PDEs: Vector- and Tensor-Valued Systems of Equations
Here in Part 9 of this course on modeling with partial differential equations (PDEs), we will learn more about setting up systems of PDEs. In particular, we will look at cases where the dependent variables represent the components of a vector or tensor field, such as the displacement vector and displacement field components in structural mechanics. These equations can be set up in the COMSOL Multiphysics® software using either the built-in interface for plane stress or a user-defined plane stress equation system defined using the Coefficient Form PDE interface. While using the predefined interface for plane stress is a lot easier, this article will focus on how to set up the corresponding equation system from scratch. This will prepare you for setting up more general systems, including systems that are not available as a built-in option in COMSOL Multiphysics®.
The Plane Stress Constitutive Relationship
For an introduction to plane stress and other 2D structural mechanics formulations, see our blog post on the difference between plane stress and plane strain. There are several different ways of formulating the constitutive equations for plane stress. We will follow the blog post and use the following notation for the relationship between stress and strain for plane stress:
with all other stress components equal to zero.
Here, the quantities are: the strain tensor components ,
, and
; stress tensor components
,
, and
; Young's modulus,
; Poisson's ratio,
; and the shear modulus
.
We will formulate the plane stress equations in terms of the displacement components and
in the x and y directions, respectively. We sometimes refer to these components collectively as the displacement vector:
In order to do so, we need the relationship between the displacement components and the strain tensor components:
where
is referred to as the engineering shear strain.
Note that to keep things simple, we will assume small deformations as well as small rotations.
Navier's Equation
The undamped version of the equation of motion for continuum mechanics is:
where is the mass density;
is an external force density, such as gravity; and
is the stress tensor.
The law of static equilibrium will give us the equations we need to formulate the PDE system for plane stress. This equation system can be viewed as a single vector-tensor equilibrium equation, formulated using the stress tensor:
representing the balance of the (internal) stress tensor, , with that of the external force density,
.
We will now recast this equation in the multivariable version of the PDE Coefficient Form:
where
and where is not a scalar but, in this case of a strongly coupled system of equations, is an elasticity tensor corresponding to the "diffusion coefficient of stress".
When setting up the equation system for plane stress using one of the Mathematics interfaces, you have several interface choices: the Coefficient Form PDE, General Form PDE, and Weak Form PDE interface. Using the Coefficient Form PDE and General Form PDE is quite elaborate, as you will see in the below derivation. A less elaborate approach is to use the Weak Form PDE, as you will see in Part 11 of this course. However, understanding the weak form requires a lot more mathematics background, so we will start by showing you how to proceed using the Coefficient Form PDE. Note that using the General Form PDE is very similar to using the Coefficient Form PDE.
Let us set up the equations for plane stress using the Coefficient Form PDE. In 3D, the components of the equilibrium equation can be written as:
For 2D plane stress, we get:
Using this form of the equation system, we can write the plane stress constitutive relationship as a tensor relationship between the stress and strain components as follows:
In the COMSOL Reference Manual documentation, in the Multiple Dependent Variables — Equation Systems section, there is a description of how to represent this type of constitutive relationship using the Coefficient Form PDE. Following this, we need to find a formulation in terms of the gradients of the dependent variables and
.
We first arrange the stress tensor as a column vector as follows:
Note that occurs twice in this column vector, corresponding to the two off-diagonal entries in the stress tensor
.
Now, we write the stress in terms of the displacement gradient components:
We need to identify the various entries in the coefficient . We can start by writing:
However, this is not good enough since we cannot obtain the right combinations of the gradient components.
To proceed, we need to take advantage of the fact that the diffusion coefficient components can further be expanded into anisotropic components:
Next, we can write the relationship as a form of the Kronecker product:
Now, compare this with
Identifying the coefficients and going back to the original Kronecker product, we see that:
We can also write this as:
and we now have the Navier's equation:
In the case of plane stress, Navier's equation corresponds to the system:
with
and
Alternatively, we can use the definition of the shear modulus and instead write this as:
Note that although the material is isotropic in this case, the diffusion coefficient of the strongly coupled PDE problem becomes (somewhat counterintuitively) anisotropic.
Boundary Conditions
The built-in interface for solid mechanics, with the plane stress option, offers several options for boundary conditions. Let us look at a few of these options and how they can be implemented using the Coefficient Form PDE.
We will start with how to implement a boundary load. For this type of boundary condition, the built-in interface provides us with Force per unit area, Force per unit length, Total force, and Pressure options.
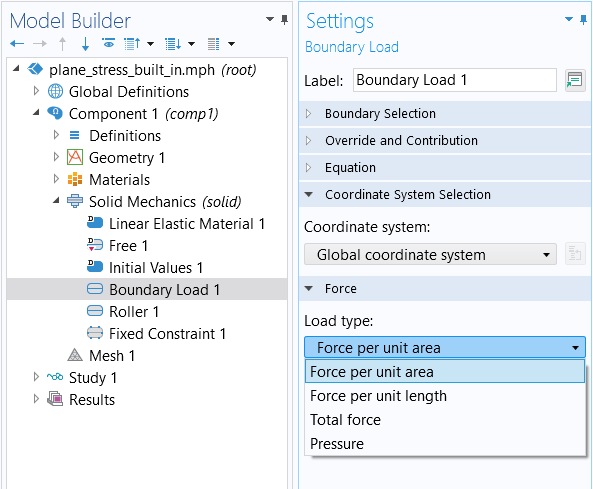
Options for the Load type settings for the Boundary Load boundary condition.
The option for specifying a Force per unit length requires us to specify two vector components:
Compare this with the Flux/Source boundary condition of the Coefficient Form PDE:
and we see that we can enter this as:
The option for specifying a Pressure requires us to give a scalar pressure :
where the negative sign on the right-hand side is due to the fact that the normal vector is defined to be directed outward from a boundary of a solid. Note that a negative pressure would then usually be called a tension.
We see that we can enter this as
Moving on to constraints, using the built-in interface, we can have a Fixed Constraint boundary condition in both displacement variables:
or component-wise:
We can also have a Roller constraint, which limits movement only in the normal direction of the boundary. This can be written in equation form as:
This is a scalar equation. We can choose to apply this constraint to the first "row" of the equation system and leave the second "row" without a constraint.
To completely constrain a boundary we could add a second constraint
where is a tangent vector. Note that in 3D, in order to completely constrain a boundary, we would need two tangential constraints using two tangent vectors. Then, you would get various types of constraints by selectively using various combinations of tangential and normal constraints. However, to fully constrain a boundary, you can, of course, more easily use the Fixed Constraint condition described earlier.
A Rectangular Plate with a Circular Hole, Using the Built-In Solid Mechanics Interface
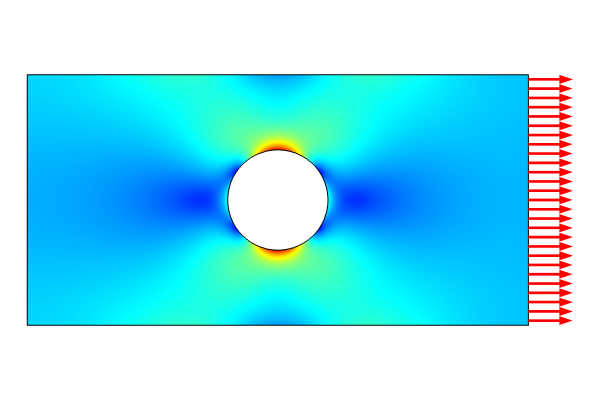
Let us now look at the example from the abovementioned blog post. The example is a simple case of a rectangular steel plate with a circular hole at the center. The rectangle is 2 m wide and 1 m tall, and the hole is centered in the rectangle and has a radius of 0.2 m.
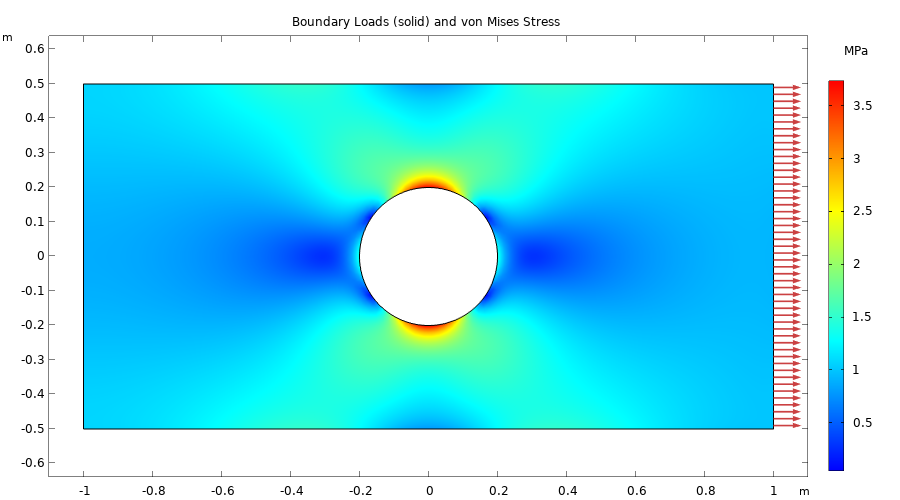
The boundary load and von Mises stress of a rectangular plate with a hole.
An extremely fine mesh setting is used to discretize the model geometry for this example, as shown in the figure below.
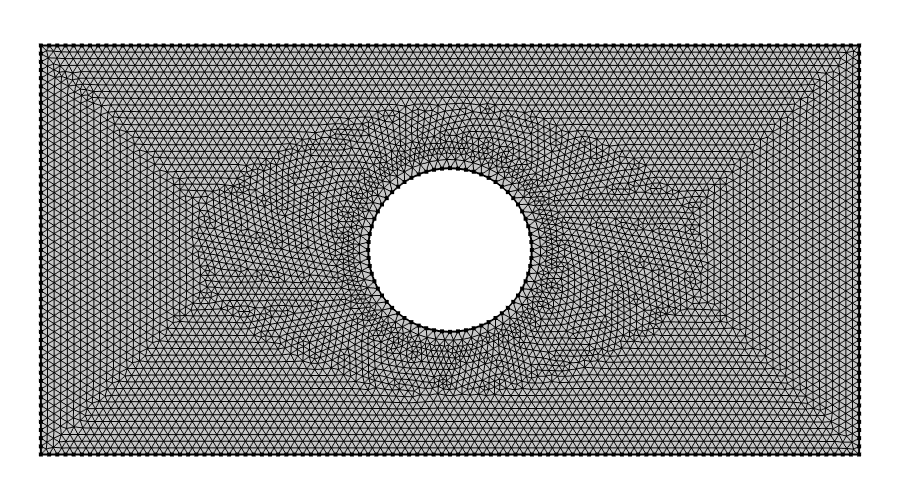
The mesh used in the rectangular plate example. The element type used is second-order triangular Lagrange elements.
In this example model, a tensile load of 1 MPa (1e6 N/m2) is applied to the right boundary, and the left boundary has a roller constraint. To avoid unwanted vertical motion, the lower-left point is fully constrained. The figures below show the settings for various parts of the interface.
 The COMSOL Multiphysics UI showing the Model Builder with the Solid Mechanics interface selected, the corresponding Settings window, and the rectangular plate in the Graphics window.
The Solid Mechanics interface with the 2D Approximation setting set to Plane Stress. The material used is Structural steel, available from the Built-In branch of the material library.
The COMSOL Multiphysics UI showing the Model Builder with the Solid Mechanics interface selected, the corresponding Settings window, and the rectangular plate in the Graphics window.
The Solid Mechanics interface with the 2D Approximation setting set to Plane Stress. The material used is Structural steel, available from the Built-In branch of the material library.
 The COMSOL Multiphysics UI showing the Model Builder with the Boundary Load boundary condition selected, the corresponding Settings window with Force per unit area selected as the Load type, and the Graphics window showing the rectangular plate.
The boundary condition settings for the tensile load.
The COMSOL Multiphysics UI showing the Model Builder with the Boundary Load boundary condition selected, the corresponding Settings window with Force per unit area selected as the Load type, and the Graphics window showing the rectangular plate.
The boundary condition settings for the tensile load.
 The COMSOL Multiphysics UI showing the Model Builder with the Roller constraint selected, the corresponding settings, and the Graphics window showing the rectangular plate.
The boundary condition for the Roller constraint.
The COMSOL Multiphysics UI showing the Model Builder with the Roller constraint selected, the corresponding settings, and the Graphics window showing the rectangular plate.
The boundary condition for the Roller constraint.
 The COMSOL Multiphysics UI showing the Model Builder with the Fixed Constraint boundary condition selected, the Fixed Constraint settings, and the Graphics window showing the rectangular plate.
The COMSOL Multiphysics UI showing the Model Builder with the Fixed Constraint boundary condition selected, the Fixed Constraint settings, and the Graphics window showing the rectangular plate.The lower-left point with a fully constrained condition.
The plots below show some of the result quantities that can be evaluated after solving.
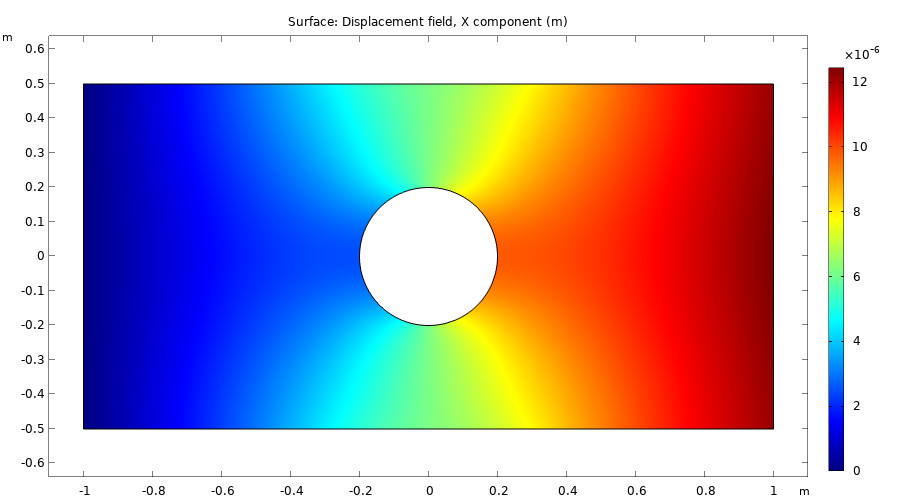
The x-displacement field, u.
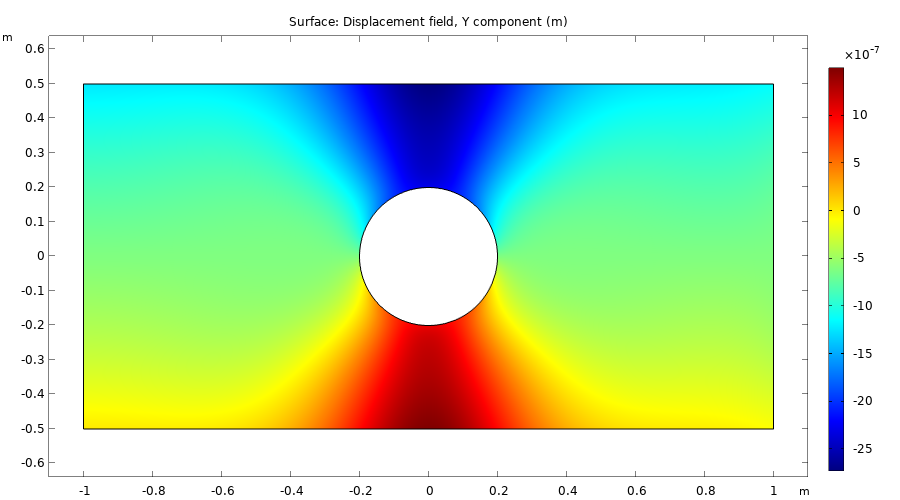
The y-displacement field, v.
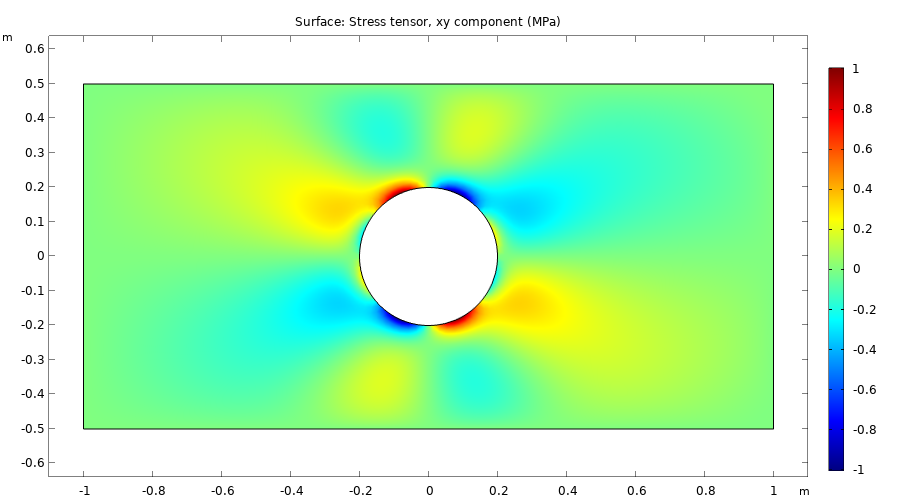
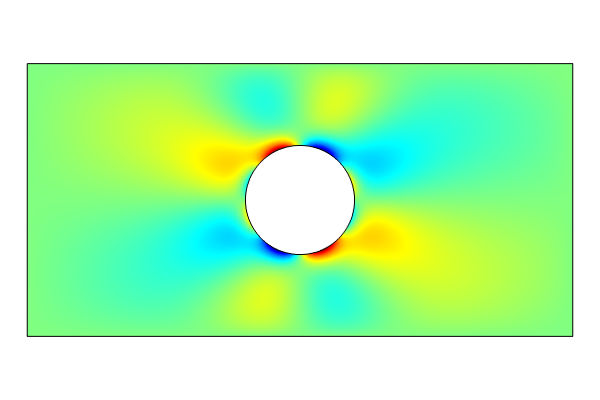
The shear stress sxy.
A Rectangular Plate with a Circular Hole, Using the Coefficient Form PDE Interface
Now, we will recreate this model using equation-based modeling.
To set up the equations for plane stress, the image below shows the Coefficient Form PDE with two dependent variables, u and v, for the displacement in the x and y direction, respectively. The default Discretization settings for Quadratic Lagrange shape functions are used. These are sometimes referred to as second-order isoparametric triangular finite elements.
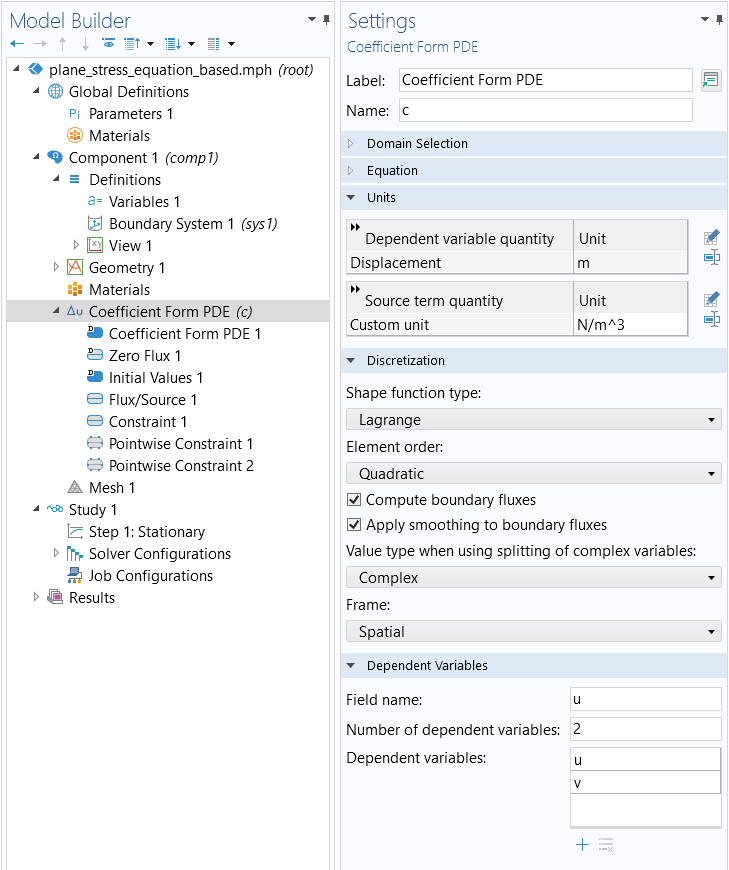
The Coefficient Form PDE settings.
In the Settings window for the Coefficient Form PDE interface, change the Units to Displacement (m) for the Dependent variable quantity and type N/m^3 for the Unit of the Source term quantity. (There is no built-in option for this unit.)
The unit option for Displacement (m).
Note that you can also determine the dependent variable and unit settings in the Model Wizard, as shown in the figure below.
The Select Physics window in the Model Wizard for changing the names and number of dependent variables as well as the units.
We will need to define some parameters for the material properties and the thickness.
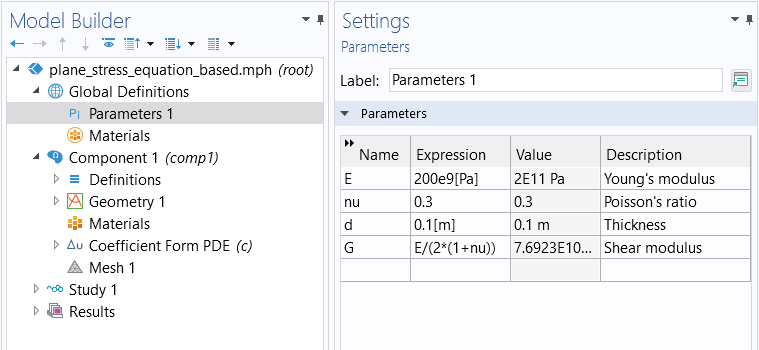
Material parameters for the plane stress example.
The thickness is not needed before or during solving, but to get the right unit when postprocessing the solution.
Recall from earlier that the diffusion coefficient for Navier's equation can be written as:
The figure below shows how to enter the diffusion coefficient components by using the Full and Diagonal options.
 The Model Builder with the Coefficient Form PDE interface selected and the corresponding Settings window with the Diffusion Coefficient, Source Term, Mass Coefficient, and Damping or Mass Coefficient sections expanded.
The Diffusion Coefficient settings for plane stress.
The Model Builder with the Coefficient Form PDE interface selected and the corresponding Settings window with the Diffusion Coefficient, Source Term, Mass Coefficient, and Damping or Mass Coefficient sections expanded.
The Diffusion Coefficient settings for plane stress.
If you have a body load , with two components
enter these in the fields for the Source Term.
The dynamic coefficients Mass Coefficient and Damping Coefficient are ignored in this model since we are using a Stationary study.
To specify the boundary load as a tensile load of 1 MPa = 1e6 N/m3, use the Flux/Source boundary condition and have = 1e6 and
= 0, as shown in the figure below
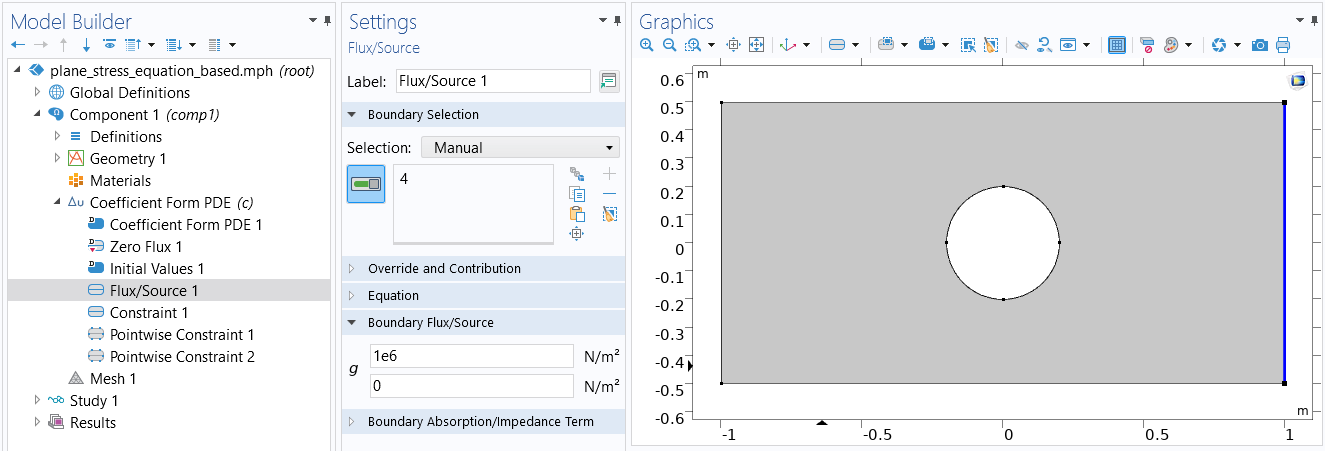
The settings for the tensile load.
In the general case, where the boundary is neither horizontal nor vertical, you can use the variables nx and ny to define boundary conditions. These variables represent the unit normal vector components, facing outward from a solid domain, on boundaries. For example, in this particular case we would get the same boundary condition by entering = 1e6*nx and
= 1e6*ny.
To specify the roller constraint, use the Constraint boundary condition with the constraint
or, written out component-wise,
nx*u+ny*v
You specify this in the fields for the general constraint
Note that since there are two equations, one each for the variables u and v, we gain access to two constraint fields. However, a roller constraint is a scalar constraint, so we only need to use one of the fields, as shown in the figure below.
 The COMSOL Multiphysics UI showing the Model Builder with the Constraint boundary condition selected, the corresponding settings, and the Graphics window showing the rectangular plate.
The settings for the roller constraint.
The COMSOL Multiphysics UI showing the Model Builder with the Constraint boundary condition selected, the corresponding settings, and the Graphics window showing the rectangular plate.
The settings for the roller constraint.
The next step is to fix the displacement of the lower-left point of the rectangle. The built-in interface provides this as one feature node with the combination of both constraints. However, to do so in the equation-based interface we need to use two Pointwise Constraint features, one for u and another for v, as shown in the figures below.
 The COMSOL Multiphysics UI showing the Model Builder with the Point Constraint boundary condition selected, the corresponding Settings window, and the Graphics window showing the rectangular plate.
The Pointwise Constraint settings for the displacement variable u.
The COMSOL Multiphysics UI showing the Model Builder with the Point Constraint boundary condition selected, the corresponding Settings window, and the Graphics window showing the rectangular plate.
The Pointwise Constraint settings for the displacement variable u.
 The COMSOL Multiphysics UI showing the Model Builder with a second Point Constraint boundary condition selected, the corresponding settings, and the Graphics window showing the rectangular plate.
The Point Constraint for the displacement variable v.
The COMSOL Multiphysics UI showing the Model Builder with a second Point Constraint boundary condition selected, the corresponding settings, and the Graphics window showing the rectangular plate.
The Point Constraint for the displacement variable v.
For convenience, we can now define a set of variables that we would like to visualize or evaluate. The figure below shows the variable settings for the strain and stress tensor components as well as von Mises stress.
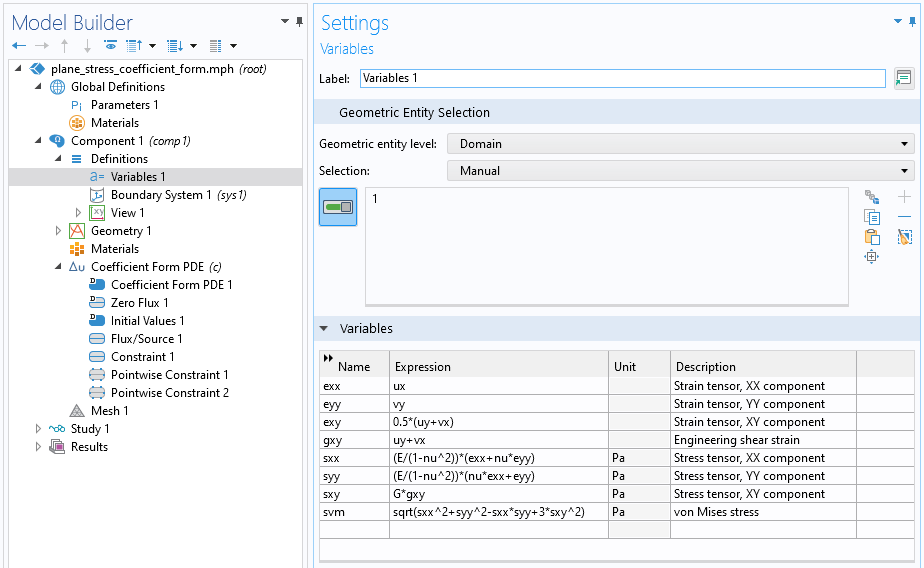
The settings for common structural analysis quantities.
If we now plot these quantities we can see that they are in perfect agreement with the results of the built-in physics interface, as expected if we have entered all the equations correctly. The figure below shows one of the stress tensor components of the equation-based plane stress solution.
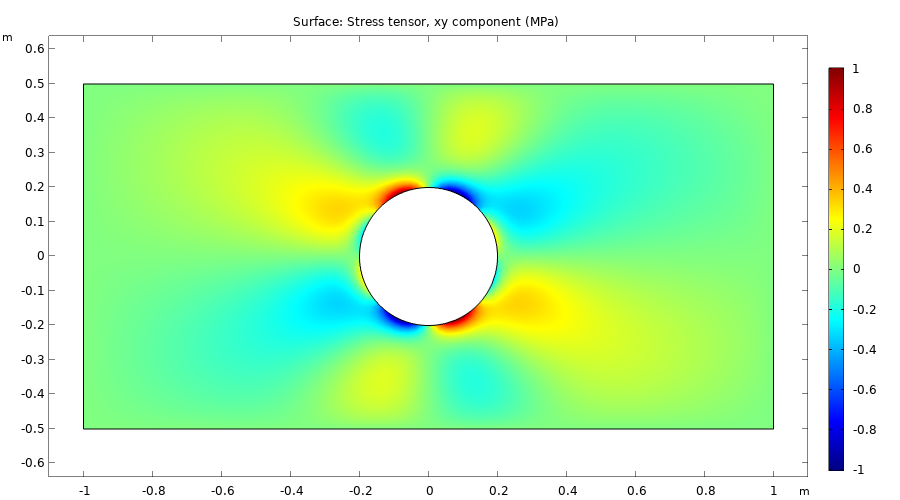
The stress tensor component sxy.
Setting up the plane stress equations using the Coefficient Form PDE requires quite a few steps. In the next couple of parts we will learn about the weak form, which provides a more compact, but also more abstract, way of modeling the same equations.
Further Learning
Although the model used as the example throughout this article is available for download, we encourage you to first build the model yourself, completely from scratch, by following the guidance provided throughout this article. Thereafter, you can open and explore the model files for both the version of the model built using the Coefficient Form PDE interface, as well as the version built using the software's predefined physics interface. This will reinforce learning how to set up equation systems from scratch.
Submit feedback about this page or contact support here.