See How Modeling and Simulation Is Used Across Industries
Multiphysics modeling and simulation drives innovation across industries and academia — as is evidenced by the many uses showcased in the technical papers and posters presented by engineers, researchers, and scientists at the COMSOL Conference each year.
Draw inspiration from the recent proceedings collected below, or, to find a specific presentation or filter by application area or conference year/location, use the Quick Search tool.
View the COMSOL Conference 2025 Collection
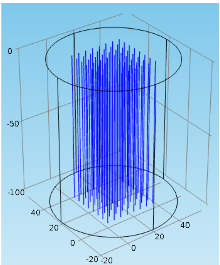
Ground-coupled heat pumps (GCHP) are successfully installed since at about 20 years in many countries to fulfill space conditioning requirements in building applications. In most cases the heat pump is connected to a system of vertical ground heat exchangers (as illustrated in Figure 1) ... Read More
An experimental program has been developed, with the purpose of evaluating the reliability in building diagnosis and characterization of an integrated analysis of several parameters related to heat transfer process through the building material. The Infrared Thermography Technique (IRT) ... Read More
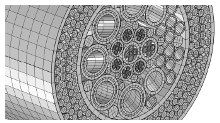
With the ever changing energy requirements & demand for better communication links across the planet, subsea umbilical & cable requirements are becoming more stringent. Where longer service life at a lower cost is now expected from manufacturers. In addition to this, with the ... Read More
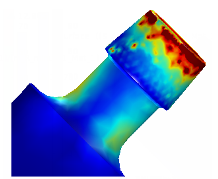
Modular orthopaedic devices are a feature of total joint replacements today. These modular orthopaedic devices allowing surgeons to choose from a variety of available implant sizes, designs & material options for the procedure required and the patient specific requirements. However, ... Read More
Spondylolysis (SL) is a defect of the spinal vertebra, and is typically caused by stress fracture of the pars interarticularis bone of the vertebral arch. It is especially common in adolescents who over train in sporting activities. Spina bifida occulta (SBO) is a malformation of the ... Read More
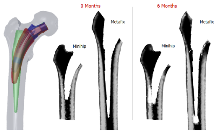
Bone resorption around hip stems, in particular periprosthetic bone loss, is a common observation post-operatively. A number of factors influence the amount of bone loss over time and the mechanical environment following total hip replacement (THR) is important. Conventional long stem ... Read More
The modeling of light propagation through multiple layers of biological tissue are assessed & compared to the theoretical predictions by Perelman at al. [94 & 95] of the most-favorable-path (MFP). The MFP on which photons will be found can be obtained from the path of the net ... Read More
This paper proposes a framework for an efficient integration between geometric modeling program and analysis tool for a coming automated aerodynamic design optimization mission. This demand can be addressed by using both in-house codes and commercial software which have the good ability ... Read More
High Pressure Processing (HPP) is a leading non-thermal food processing technology that is often cited as a major technological innovation in food preservation. Although it is very early to place this emerging technology among the list of breakthroughs in food processing, HPP has started ... Read More
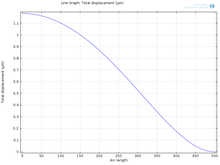
In this work, a MEMS based condenser microphone [1,2] using Polyimide as the diaphragm has been designed. The microphone structure has a backplate placed on top of the diaphragm. The backplate and the diaphragm are made up of polyimide. The two polyimide plates are separated by air gap ... Read More