
Swept meshing is a geometry discretization technique available in COMSOL Multiphysics for specific types of geometries, including thin geometries, geometries with bends, and models with little or no variation in a specific direction. A swept mesh starts at a source boundary and sweeps along to a specified destination boundary. In previous versions of COMSOL Multiphysics, the source and destination boundaries generally needed to be specified by the user. However, in the latest release, COMSOL Multiphysics version 4.3b, the swept mesh has become more automated, minimizing the number of source and destination boundaries manually defined.
Swept Meshing, and Its Advantage
Meshing is one of the bases of finite element analysis. Knowing which type to use in different situations is crucial for accurate and fast simulations. Swept meshes are especially useful for thin geometries, because other (tetrahedral and triangular) meshes create more elements than necessary to account for the skewed dimensions that exist within a thin geometry. The swept mesh creates hexahedral (default) or prismatic mesh elements, which can still effectively handle the disproportional dimension sizes, with far less elements.
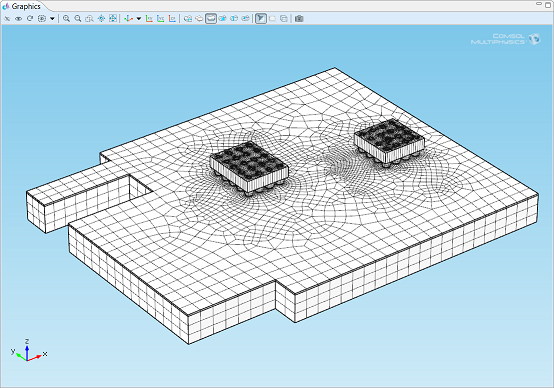
Circuit board model with a swept mesh with 37,027 3D domain elements, automatically generated with
COMSOL Multiphysics 4.3b.
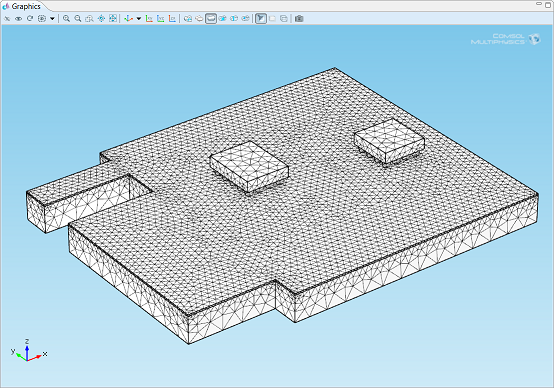
Circuit board model with a tetrahedral mesh with 56,966 3D domain elements: an example of
over-meshing.
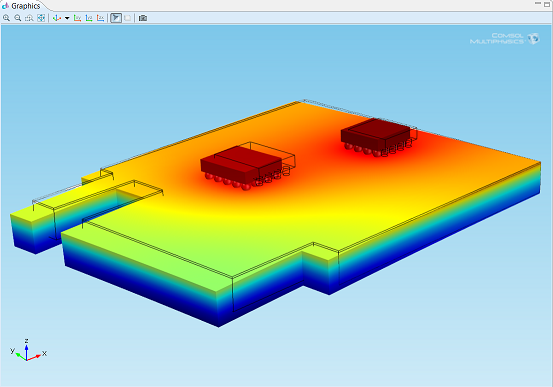
Temperature distribution and deformation of the circuit board.
The denser the mesh, the greater the simulation time, which is unnecessary if changes in the physical properties are minimal in well-meshed regions. In the figure above, the term “over-meshed” is used, as the top plate has an overabundance of elements, while not a lot is actually happening in large regions of this top plate. In addition to this, the tetrahedral mesh is too coarse in the two plates above the solder joints, where changes in the physical properties are more pronounced. Using the swept mesh will lead to results that are both accurate and swift. In this case, second-order elements are used for the thermal analysis which is a good compromise between accuracy and computational efficiency.
New Semi-Automatic Swept Meshing Functionality
With the release of COMSOL Multiphysics 4.3b, the swept mesh can also be created automatically in most cases, without the need to manually define source and destination surfaces for certain types of geometries, such as this one. Since this is all done in the COMSOL environment, you can use swept meshes for any type of simulation: structural, heat, CFD, acoustics, electromagnetics, chemical, and more. COMSOL always endeavors to produce the most powerful, easy-to-use software for our customers to achieve accurate simulation results, and we are certain that this new functionality shows that commitment.





Comments (4)
Ivar Kjelberg
May 10, 2013Nice example of enhancements for 4.3b, looking forwward to use them
One comment though: I understand the over-meshing argument in the X-Y horizontal plane, but one could still ask the question: is one element in the *thickness” along Z really sufficient ?
If this is a transient case, then the alpha=k/(rho*Cp) (that you have now introduced as a predefined variabele, thanks for that) could be used to check the mesh density in the different directions, compared to desired time steps. Just as done classically for CFD.
Sincerely
Ivar
Bjorn Sjodin
May 10, 2013Thanks for your feedback. The swept mesh in the thin plate actually has 3 second order elements through its thickness. The picture resolution makes this difficult to see.
Muhammad Gulzari
March 4, 2018Dear Andrew Griesme,
How one can identify that mesh applied on certain geometry is good enough, like in my case I am working on thin square plate problem which has two small squares as well. Of course one key identifier is mesh convergence plot, but how i can decided for what type of geometry, what type of mesh is perfect? How I can get mesh convergence plot although I searcher a lot inside the forum but did not find any proper way
Thank you
Caty Fairclough
March 29, 2018Hi Muhammad,
Thanks for your comment.
For your question, you may find this blog post helpful: https://www.comsol.com/blogs/how-to-inspect-your-mesh-in-comsol-multiphysics/
You can also find out more by contacting our Support team.
Online Support Center: https://www.comsol.com/support
Email: support@comsol.com