
COMSOL’s Optimization Module is a powerful tool for improving the performance of your devices and systems. Here, we will look at optimizing the power applied to two heaters in a flow channel with the objective of heating up the fluid as much as possible as it passes through the channel, while constraining the peak temperature at the heaters themselves. One application of this technique is improving the efficiency of thermal processes.
Heating up a Fluid, a Thermal Processing Scenario
Let’s consider a very simple case of a fluid passing through a channel, with a couple of heaters on the sides of the channel. The objective of the heaters is to heat up the fluid as much as possible, but to keep the temperature at the surface of the heater below a specified value. For this example, we will consider the fluid to be air, coming into the channel at 20°C, and we want to keep the temperature at the surface of the heaters below 95°C.
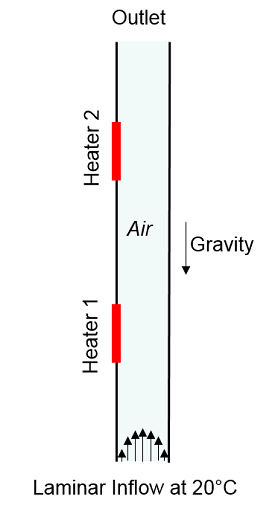
We start our modeling by using the Non-Isothermal Flow interface. This allows us to set the Inlet velocity and Temperature, and an Open Boundary at the outlet. The other boundaries of the channel are left at the default “Wall, no Slip” and two Heat Fluxes of 5W each are applied to two of the channel boundaries. The Volume Force adds a buoyancy term, which acts to accelerate the flow due to the vertical orientation of the channel.
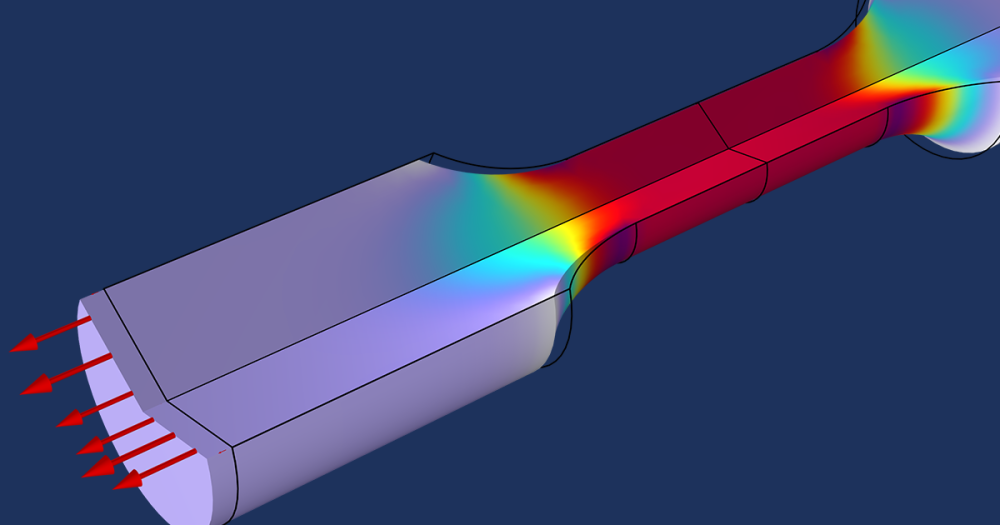
Once we solve this model, we can examine the velocity and temperature field:
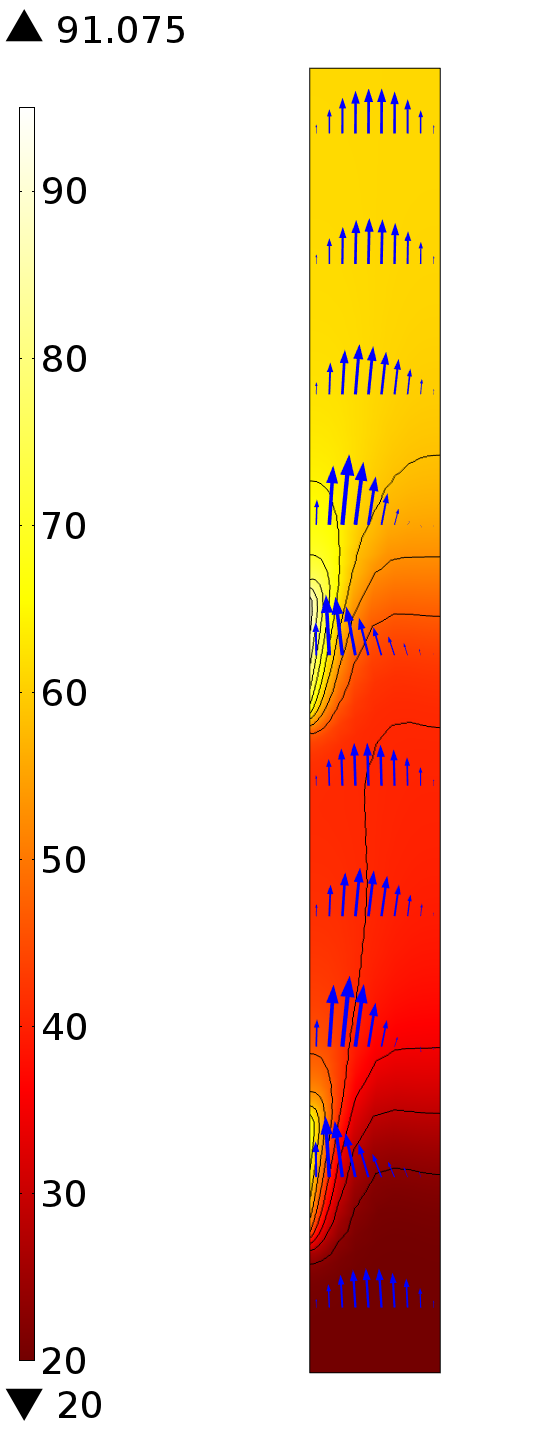
The Non-isothermal Flow interface automatically sets up a useful postprocessing variable at the Open Boundary: the mass-flow-weighted temperature, comp1.nitf.open1.Tave. This variable accounts for the non-uniform velocity at the outlet, as well as any density changes in the fluid. This weighted temperature average over the outlet boundary is about 61°C, while the maximum temperature at the heaters is just above 90°C. The objective of our optimization will be to get the weighted temperature at the outlet as hot as possible, while keeping the heater temperature below 95°C.
Setting up the Optimization Problem in COMSOL
The above scenario can be solved with the Optimization Module using the Nelder-Mead optimization algorithm. The Nelder-Mead algorithm can consider an objective function that is reasonably smooth with respect to the design variables, and constraints that depend upon the computed solution can be included, as well as bounds on the design variables. Let’s take a look at how this is set up.
We start by adding an Optimization interface to the Study branch, which defines the objective function, the constraints, and the design variables.
The Nelder-Mead optimization algorithm is used, with all default settings.
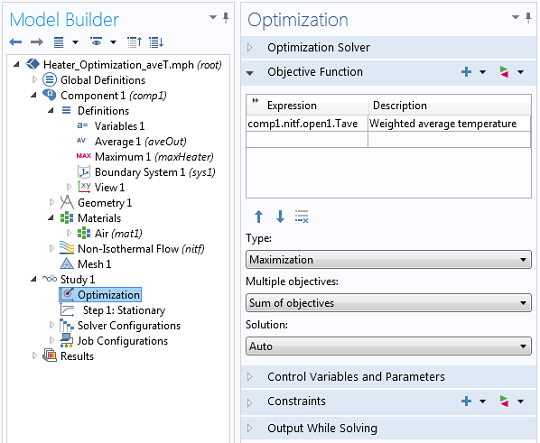
The objective function is to maximize the mass-flow-weighted average temperature at the outlet.
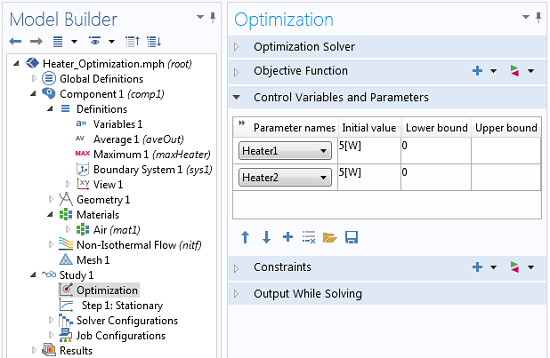
The design variables are the heater power.
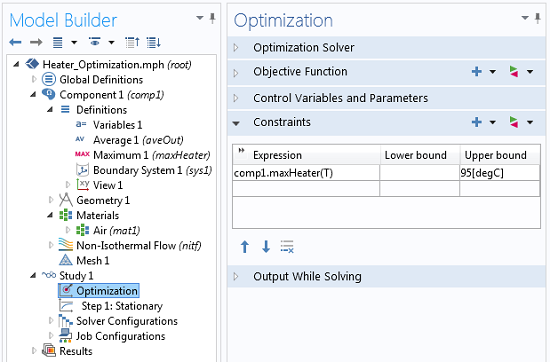
Constraints are applied on the maximum temperature at the heaters.
The global objective is the average temperature at the outlet and the constraint is that the temperature of the heaters stay below 95°C. The two control variables are Heater1 and Heater2, which are Global Parameters used to define the total power at each heater. A lower bound of 0 W is specified, and no upper bound is given. With the set-up as shown, we can compute the solution.
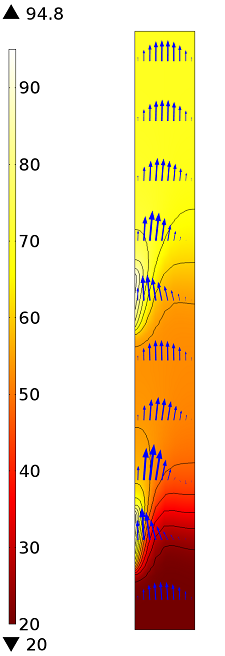
After running the optimization, we can see that the peak temperature at the heaters stays below 95°C. The weighted temperature at the outlet is just under 70°C, and the power at the first and second heaters is 7.9 W and 4.0 W respectively.
Conclusion
The Optimization Module was used to find the heater power that will heat the air as much as possible while keeping the peak temperature at the heaters below a specified value. This approach is useful for process control modeling and optimization. Please contact your local sales representative if you would like to receive this model.



Comments (2)
Amer Al-Damook
July 5, 2015fantastic !!
could I get the download the application files of this tutorial, please??
Walter Frei
July 6, 2015Dear Amer,
Please contact COMSOL Support and this file can be sent out.