The Application Gallery features COMSOL Multiphysics® tutorial and demo app files pertinent to the electrical, structural, acoustics, fluid, heat, and chemical disciplines. You can use these examples as a starting point for your own simulation work by downloading the tutorial model or demo app file and its accompanying instructions.
Search for tutorials and apps relevant to your area of expertise via the Quick Search feature. Note that many of the examples featured here can also be accessed via the Application Libraries that are built into the COMSOL Multiphysics® software and available from the File menu.
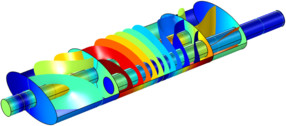
This model simulates the pressure wave propagation in a muffler for a combustion engine. It uses a general approach for analysis of damping of the propagation of harmonic pressure waves. The model is solved in the frequency domain and provides efficient damping in a frequency range of ... Read More
This tutorial series describes in two different ways how to organize a more complex geometry. Read More
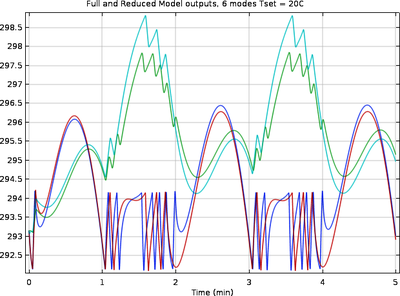
Large FEM simulations can be costly and, if repeated simulations are needed, it can be beneficial to use reduced-order models (ROMs). ROMs are typically valid only in the vicinity of their design conditions and have lower accuracy, but the simulation time is significantly shorter. The ... Read More
This model couples the Navier Stokes equations and the heat transfer equations to examine density driven flow of free fluids. Here the fluid is in a square cavity with a heated wall. The buoyancy force is a Boussinesq term added to the Navier-Stokes equations. The equation is ... Read More
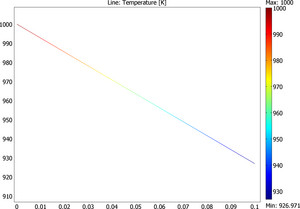
The example shows a 1D steady-state thermal analysis including radiation to a prescribed ambient temperature. The temperature field from the solution of this benchmark model is compared with a NAFEMS benchmark solution. Read More
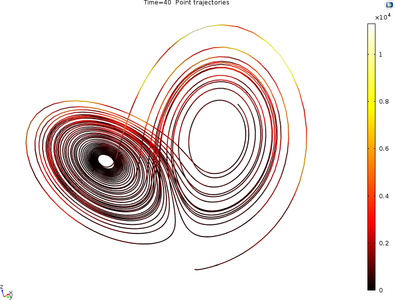
A Lorenz attractor can be described by a system of ordinary differential equations: the Lorenz system. In the early 1960s, Lorenz discovered the chaotic behavior of this system for certain parameter values and initial conditions. The solution, when plotted as a phase space, resembles the ... Read More
In modeling of transport by diffusion or conduction in thin layers, we often encounter large differences in dimensions of the different domains in a model. If the modeled structure is a so-called sandwich structure, we can replace the thinnest geometrical layers with a thin layer ... Read More
Global equations are a way of adding an additional equation to a model. A global equation can be used to describe a load, constraint, material property, or anything else in the model that has a uniquely definable solution. In this example, a structural mechanics model of a spring is ... Read More
The Shallow Water equations are frequently used for modeling both oceanographic and atmospheric fluid flow. Models of such systems lead to the prediction of areas eventually affected by pollution, coast erosion and polar ice-cap melting. Comprehensive modeling of such phenomena using ... Read More
This model illustrates the use of COMSOL Multiphysics for modeling of ionic current distribution problems in electrolytes, in this case in human tissue. The problem is exemplified on a pacemaker electrode, but it can be applied in electrochemical cells like fuel cells, batteries, ... Read More