Modeling Approaches in Heterogeneous Catalysis

Modeling of heterogeneous catalysis traditionally attracts great interest from the chemical engineering community, due to the many industrial processes that utilize this type of catalysis. Here, we discuss the procedure of starting with detailed micro-geometries and then proceeding with approximations through homogenization. By following this procedure, from the microscopic particle level to the macroscopic reactor level, we can design the catalyst in detail and study the influence of this design on the total reactor performance.

Introduction to Heterogeneous Catalysis

Motivated by the enormous amount of production of bulk and fine chemicals and the large-scale removal of environmentally harmful chemicals in processes based on heterogeneous catalysis, the science and engineering community is very interested in this subject. There is also a large focus on understanding these processes through mathematical modeling and simulations.

Heterogeneous catalysis concerns catalytic reactions at the interface between two different phases. Here, we limit our discussion to heterogeneous catalysis at solid-fluid interfaces, which is the most common form of heterogeneous catalysis in industrial processes. In such processes, reactants and products are present in a fluid mixture in contact with a solid catalytic surface where the catalytic reactions take place.

Common large-scale industrial processes based on solid-fluid heterogeneous catalysis include the production of ammonia in the Haber-Bosch process, nitric acid in the Ostwald process, ethylene oxide in the Wacker process, hydrogen by steam reforming, and polyethylene and polypropylene in Ziegler-Natta polymerization.

Electrochemical reactions at the surface of electrocatalysts are also categorized under heterogeneous catalysis. Examples of large-scale industrial processes based on electrocatalysis are the chlor-alkali, chlorate, and water splitting processes.

The catalytic converter used in the automotive industry, where one of the steps is the reduction of nitrogen oxides to nitrogen and oxygen, is another example of a widely used process based on heterogeneous catalysis. Other important processes from an environmental point of view are desulfurization of petroleum and the catalytic oxidation of sulfur dioxide, both with the ultimate goal of reducing the emissions of sulfur oxide to the environment during combustion of petroleum products.

Sensors that are able to detect very small amounts of adsorbed molecules are often based on heterogeneous catalysis. Hydrogen and oxygen sensors are examples of such sensors working through electrocatalysis, as are biosensors based on enzymatic reactions.

The Main Steps

Catalysts in heterogeneous catalysis act in the same way as in homogeneous catalysis — by lowering the activation energy for the catalyzed reactions.

We will not discuss how catalysts actually achieve this, but we can briefly mention that most processes involve two types of solid catalysts: Acid and metal catalysts (as per G. F. Froment, K. B. Bischoff, J. De Wilde in Chemical Reactor Analysis and Design). Acid catalysts, such as aluminosilicates, may act as Lewis or Brønsted acids and in this way form a surface complex with lower activation energy. Metal catalysts are mainly concerned with hydrogenation and dehydrogenation reactions involving a surface complex of adsorbed hydrogen.

The main steps for chemical species in heterogeneous catalytic reactions can be described as follows (as per Chemical Reactor Analysis and Design and H. S. Fogler’s book Elements of Chemical Reaction Engineering):

1. Transport of the reactants from the bulk of a mixture to a catalyst particle
2. Transport of the reactants in the pores of the catalyst particles to an active site
3. Adsorption of the reactants to the active site
4. Reaction of reactants to form an adsorbed product
5. Desorption of the product from the active site
6. Transport of the products in the pores of the catalytic particle out of the particle
7. Transport of the products from the particle to the bulk of the mixture

The figure below shows these seven steps schematically in a cross section of a catalyst particle. The catalyst particle consists of the grains of the catalyst support. The active sites are colored in apricot and are positioned at the surface of the catalyst support (blue pattern).

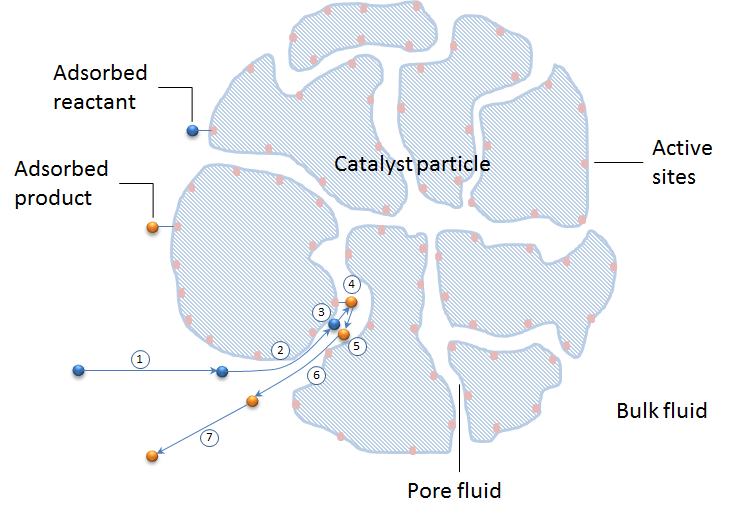
Let’s look at the possible modeling approaches for these seven steps. We can also study how the seven steps are included in a model of a whole catalytic reactor, including the material balance in the bulk of a reacting mixture.

Adsorption-Desorption Models

There are two main types of adsorption: Physisorption and chemisorption.

Physisorption occurs through van der Waals forces, while chemisorption involves covalent chemical bonds. In heterogeneous catalysis, chemisorption is usually a necessary part of the catalytic reaction. Therefore, this is the only type of adsorption that we discuss here.

The most common description of chemisorption in heterogeneous catalysis is through the Langmuir isotherm. The theory for the Langmuir isotherm is based on the following assumptions:

1. Adsorption is energetically uniform for different adsorption sites and at different surface coverages
2. The adsorbed species are assumed to form a monolayer
3. There is no interaction between adsorbed molecules

Here, surface coverage refers to the fraction of adsorption sites occupied.

The Freundlich isotherm is based on the assumption that adsorption is nonuniform with some sites having higher adsorption coefficients and so being covered by molecules first. These sites have a more exothermic heat of adsorption. The heat of adsorption depends logarithmically on the surface coverage. The Temkin isotherm can be obtained by assuming a linear dependency of the heat of adsorption on the surface coverage. Other adsorption models such as the BET isotherm also include multiple layers of molecules, which have to include physisorption in their description.

Surface Reactions

According to Elements of Chemical Reaction Engineering, three possible reaction mechanisms are often used in the modeling of heterogeneous catalysis:

Single-site reaction mechanisms describe the adsorption of a molecule and its isomerization or decomposition on this single site. The figure below shows an example of molecule isomerization.

Dual-site reaction mechanisms describe the adsorption of a reactant molecule that then interacts with another free site on which the product is adsorbed. A dual reaction mechanism may also describe the adsorption of two reactants on different sites, where the adsorbed species then react to form the product, as in the figure below.

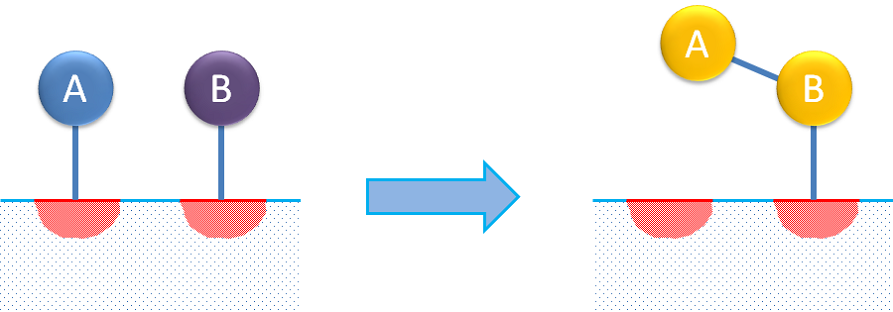
Dual- and single-site reactions are usually considered to follow Langmuir-Hinshelwood or Hougen-Watson kinetics.

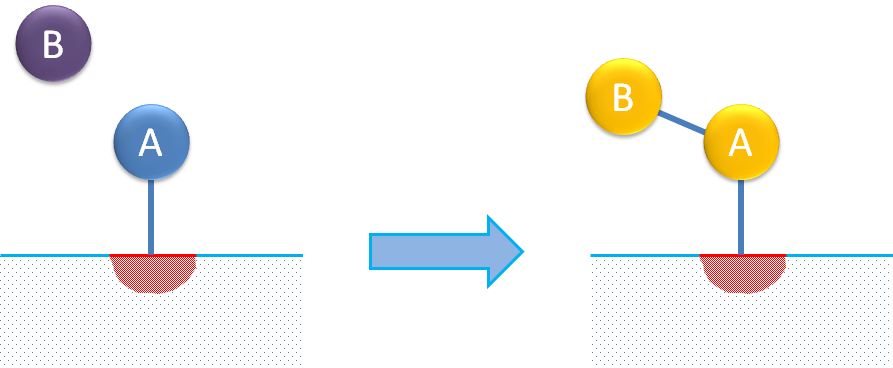
A third surface reaction mechanism describes the adsorption of a reactant molecule on a single site where the adsorbed species reacts with a molecule in the fluid (not adsorbed) to form the adsorbed product. This is usually referred to as the Eley-Rideal mechanism.

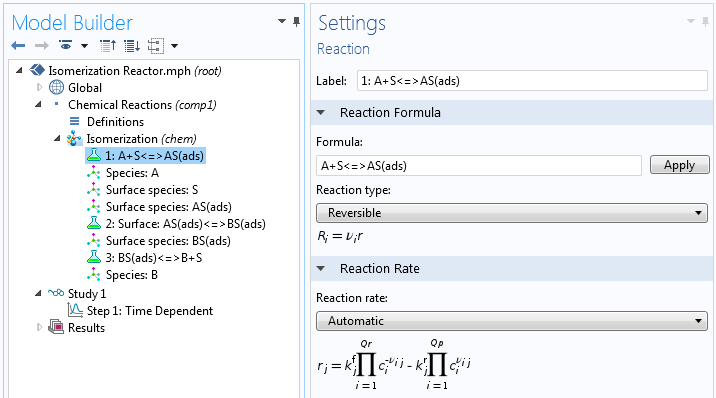
Even for the simplest possible single-site reaction mechanism, the overall rate expression may be relatively complex when expressed analytically as a single expression. We can look at the example of isomerization according to the following total reaction:

(1)

The reaction mechanism may be expressed as follows:

(2)

Here, S denotes the active site, AS(ads) the adsorbed reactant, BS(ads) the adsorbed product, and B the product.

The reaction rate expression even for this simple mechanism, using the law of mass action and the simplification that reactions 1 and 3 are close to steady state, is relatively complicated (as shown by G. F. Froment, K. B. Bischoff, and J. De Wilde in Chemical Reactor Analysis and Design):

(3)

In this equation, \theta denotes the surface concentration of unoccupied active sites, {c_A}, and {c_B} are the concentrations of isomers A and B respectively. {K}, {k_1}, {k_2}, and {k_3} are constants.

When using numerical methods, we do not have to derive a total rate expression for the mechanism. In this case, we can just type in the chemical equations for the mechanism. Instead, we have to give estimates of the rate constants for each of the steps and also an estimation of the surface concentrations at the start of the process.

The combination of deriving an analytical expression and entering the full reaction mechanism, without any simplifications, is also a good alternative. The reason is that the analytical expression contains products of constants and intermediate concentrations that can be obtained from measurements of the total reaction rate of the reaction. We can use these products to estimate the reaction rates for all steps in the detailed mechanism. In addition, this combined approach gives us the possibility to investigate under which conditions the simplifying assumptions are valid and when we have to use the full set of reactions in a model.

The Transport Steps

The description of the transport in the bulk and in a porous catalyst may be done at the particle level at a microscopic scale, where the catalyst particles and pore geometry are described in detail. In addition, when the catalyst is very active, then a porous structure is not required and the geometry can also be described in detail.

However, when the pores are very small compared to the size of the typical representative unit cell of the catalyst geometry, or the number of the pores in this unit cell is too large, a detailed geometrical description of the porous catalyst is not viable. At this stage, we can use a homogenized description of the porous catalyst structure.

Let’s assume that we treat the microstructure of the catalyst with a homogenized model. We can still describe the structure made up of the particles using a detailed model when we study the transport in the bulk mixture in the whole reactor.

When the number of particles becomes too large and the geometry of the particle bed becomes too complex, homogenization at the scale of the bulk mixture has to be used as well.

Let’s have a look at these four possible modeling approaches:

1. Detailed description of the microscopic catalyst structure
2. Homogenized description of every particle
3. Detailed description of the structure of many particles where the description of the individual particles is homogenized
4. Homogenization of the particle bed in combination with homogenized description of the particles

Microscopic Scale

The possibility of modeling very complex irregular structures has increased with the development of X-ray microtomography and the computing performance available for engineers and scientists working with modeling and simulations.

A small part of a porous catalyst in a battery.

In addition, the ability to manufacture microstructures with well-defined catalyst and pore geometries has also increased the interest for studying these regular structures using their detailed geometry. Let’s look at a hypothetical example of a catalyst particle constructed of a regular geometry of channels, according to the figure above. The geometry consists of around a hundred overlapping catalyst grains that together form a spherical catalyst particle of about 10 micrometers in diameter. The voids between the catalyst’s grains form a tortuous microchannel system.

The equations for the material balances describe the accumulation and flux balance in the domain. The adsorption, reaction, and desorption processes are described as boundary conditions at the surface of the catalyst grains. The grains themselves are not part of the modeling domain; only the fluid outside the particles and the fluid in the pores inside the particles are part of the modeling domain. The material balance for a species, _i, in the fluid in the absence of homogeneous reactions is:

(4)

Here, {{\bf{N}}_i} denotes the flux vector for species _i.

The flux of species at the boundaries that represent the catalyst surface is then given by the reaction rate, R_i, for the consumption or production of species _i in the catalytic reaction:

(5)

where {\bf{n}} represents the outwards normal vector to the surface of the catalyst.

The figure below shows the results of a simulation of the flow around a particle and the concentration of the reactant. The surface plot shows the concentration of a species that reacts at the surface of the catalyst grains. The streamlines show the velocity field.

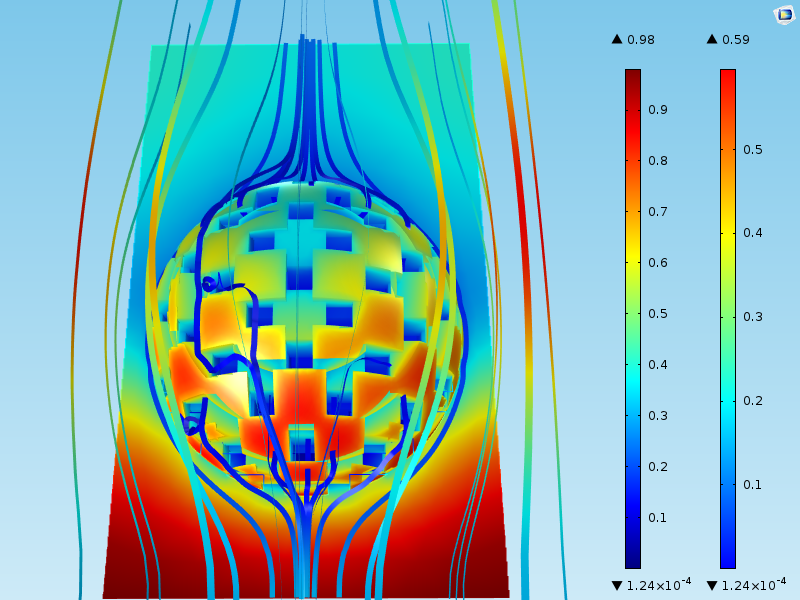
We can see that the concentration in the bulk around the particles varies between 0.98 mol/m³ at the inlet (at the bottom of the domain) to around 0.4 mol/m³ at the outlet (at the top of the domain). Furthermore, the highest concentration at the catalyst grain surface, which is found at the bottom of the sphere, is 0.59 mol/m³. This means that even when the fluid first makes contact with the catalyst particle at the lower part of the sphere, there is a mass transport boundary layer where the concentration varies by about 0.30 mol/m³ (= 0.98-0.59).

The concentration difference between the bulk and the surface of the sphere varies around the spherical catalyst particle. This mass transport boundary layer corresponds to Step 1 in the list outlined in the “Main Steps” section above.

Not all of the reactant molecules are consumed at the outer surface of the catalyst particle. Some of the molecules diffuse into the porous structure to later adsorb and react at the surface of the pore walls, i.e., the surface of the catalyst grains inside the porous particle. This transport process corresponds to Step 2 in the list.

Homogenization at the Microscopic Scale

If we want to model a large number of particles, then we cannot afford to model the geometry in the same level of detail as shown above. In that case, we may model the porous structure through homogenization. Essentially, this means that we treat the porous particle as a homogeneous slab containing both the fluid and the catalyst. The fluid is modeled using the porosity in the description with effective transport properties that depend on the porosity and tortuosity of the particles.

After homogenization, the adsorption, reaction, and desorption processes become sources and sinks in the material balances. In other words, they are no longer described as boundary conditions to the fluid domain. Instead, the reactions are represented as sources or sinks in the porous domain of the catalyst particles.

(6)

In this equation, {S_a} represents the specific catalytic surface area of the particles, which is the surface area per unit volume.

In addition, we now have two different modeling domains with two different sets of domain equations: One for the bulk fluid surrounding the particle, without the catalytic reaction term, and one for the porous particle. In the internal boundaries between these two domains, we have continuity in concentration and in flux of chemical species.

We also find continuity in the fluid flow equations, which for the bulk fluid are described by the Navier-Stokes equations, while the Brinkman equations may describe the fluid flow in the porous domain.

The figure below shows the flow field and the concentration at the surface and around a homogenized particle. Note that the surface now only shows the concentration at the outer surface of the porous pellet. In the detailed case above, the surface plot represented the surface of the grains all the way into the center of the particle.

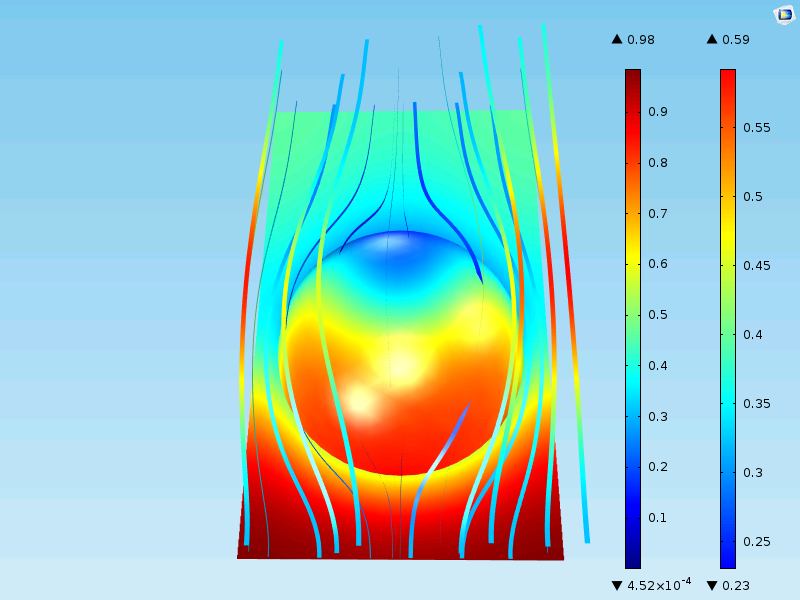
The results are close to those including the full geometrical description. The maximum concentration at the surface of the pellet is 0.59 mol/m³ and the minimum is almost 0 mol/m³ in the middle of the particle, just as in the case with the detailed description. Also, the outlet of the unit cell is about 0.40 mol/m³, as in the case for the detailed description.

Why is there decent agreement? Well, it’s because the catalyst grains in the detailed geometry are relatively small compared to the total size of the particle. When the catalyst grains become larger and more irregular in shape, homogenization becomes a less accurate description.

It may also be interesting to look at the concentration inside of the particle in the homogenized case and in the detailed case. The figure below shows that the concentration distribution in the particle is also decently described in the homogenized model. It is extremely important that the homogenized model gives a good description of the transport and reaction inside the particles if we want to use it for design purposes. The reaction distribution gives us a picture of how much of the internal parts of the catalyst are used in the adsorption, reaction, and desorption processes. If the internal parts are not used, then we are actually wasting a lot of catalyst material and we may instead use a nonporous catalyst, like in the monolithic reactors. For very active catalysts, we usually do not need the enlarged surface area provided by the porous particles.

Detailed Description in the Macroscopic Scale of Many Homogenized Particles

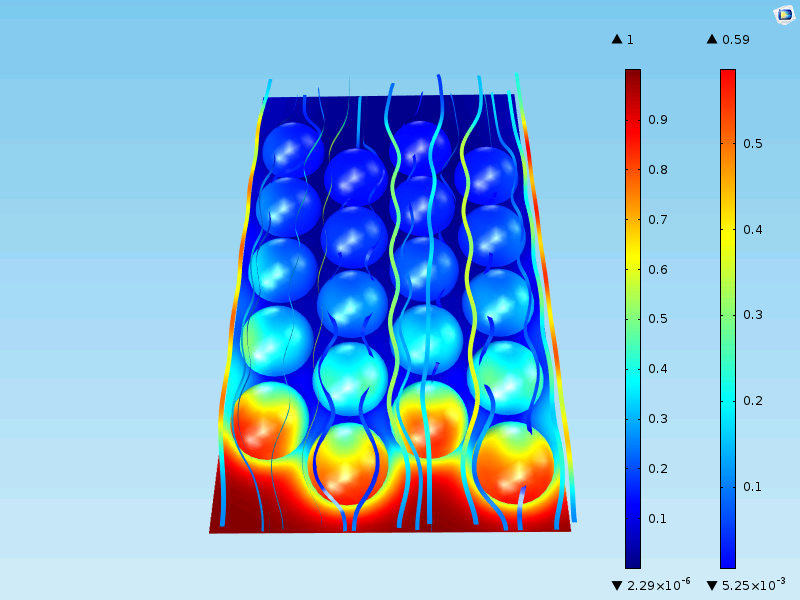
Once we know that a homogenized particle model gives us a decent approximation of the detailed geometry, we may use this approximation for describing a large number of particles in a fixed bed reactor. An example may be a micro-reactor, where the detailed geometry may be constructed using microtechnology. Such reactors may be used for detailed kinetic studies and for lab-on-a-chip (LOC) devices.

Also, in this case, we have two types of domains: One for the bulk fluid and one for the porous particles. We also find continuity in flux and concentration across the internal boundaries between the bulk fluid and the porous particles.

Now, the concentration decreases to small values in the bulk mixture outside of the catalyst particles as well. The maximum concentration at the surface of the particles is still the same, 0.59 mol/m³. That is to be expected, as the first row of particles experiences an inlet that is almost identical to the single-particle model above.

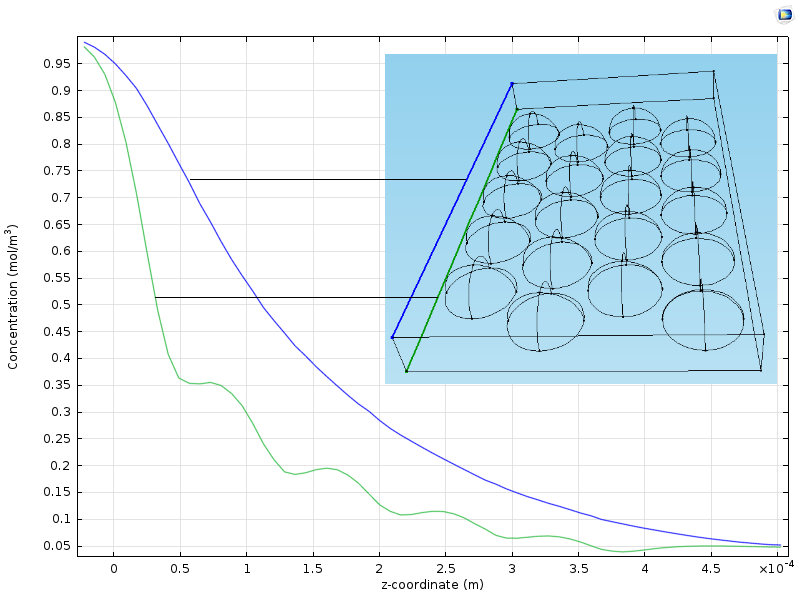
The figure below shows two plots of the concentration from the inlet to the outlet along two vertical lines. One line runs in a plane slightly above the particles and another runs in a plane along the position of the center of the particles. We can see that the curve along the line closer to the particles (green) reveals the position of the particles with its wavy pattern. The concentration curve along the line a bit further from the particles is smooth because it is smoothed by diffusion. The average concentration along the reactor, from the inlet to the outlet, is somewhere in between the green and the blue curves.

Homogenized Description in the Macroscopic Scale

In the example above, we introduce a first homogenization for the inner parts of the catalyst particles. See the figure below:

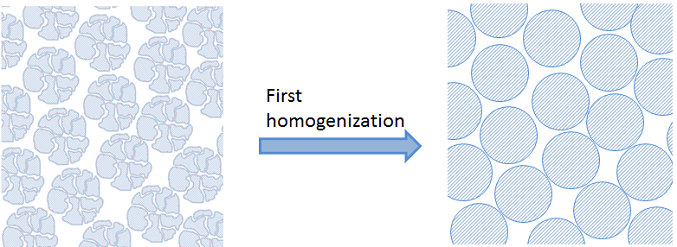
When there are too many particles in a fixed bed reactor, the particles are also very small in comparison to the dimension of the fixed bed. In that case, we cannot afford to describe the detailed geometry of the bed. Instead, we may use a second homogenization for that and the bulk fluid in the fixed bed.

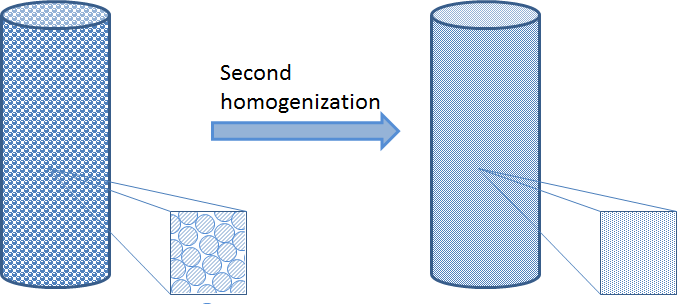
Since the porous particles are very small compared to the size of the bed, we can collapse the particles to sources and sinks in the porous bulk domain. However, in this homogenization, we have to keep the description of the transport across the boundary layer that surrounds every particle and the transport-reaction process inside the porous particles. We also have to keep the approximate description of the transport and the flow in the porous bulk domain. See the figure below for the principle depicted on the non-homogenized particles. We can achieve this by introducing an independent variable, r, in every point in the fixed bed, which corresponds to the radius of the porous particles, including the boundary layer just outside of this particle.

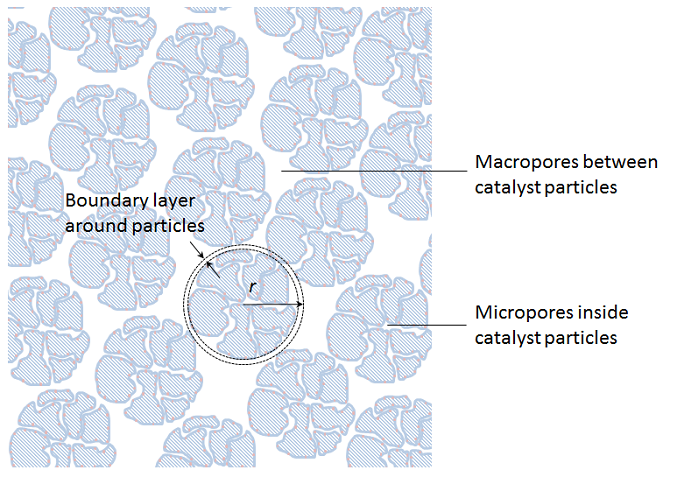
The transport in the boundary layer and the transport reaction process inside the particles is then approximated with a spherically symmetrical material balance along the radius. The advective flux in the detailed models in our example above mainly runs axially (in the direction down-up across the particle), while the second homogenization only accounts for radial variations in the particles. However, some of this advection may be accounted for as a slightly increased effective diffusivity, which gives dispersion in addition to molecular diffusion in the simplified description.

If we model the fixed bed in three dimensions, this actually means that we obtain four independent space variables: x, y, z, and r for the variable along the particle radius. The fifth independent variable is time. In addition, we have to use a so-called bimodal porosity description, which describes the micro-porosity inside the catalyst particles and a macro-porosity for the void between the particles where the bulk mixture flows (see the figure above).

The coupling between the 1D transport-reaction equations at the particle level and the bulk of the fixed bed is obtained by introducing the flux in and out of the porous particles as sources and sinks in the porous bulk domain. Conversely, the local concentration in the bulk domain is the boundary condition for the concentration at the boundary layer in the particle model in every point in the porous bed.

For steady-state models with relatively simple reaction kinetics described as a polynomials of one concentration, the transport reaction process along the radius of the particle (including the boundary layer) may be solved analytically. This solution is tabulated for different types of particles and kinetic reaction orders by using the Thiele modulus and the so-called effectiveness factor. In such cases, the analytical expressions for the flux in and out of the porous particles are used as sources and sinks in the material balance for the bulk of the fluid in the fixed bed.

Also, at the macroscopic scale, the accuracy of the homogenized approximation depends on the relative size of the particles compared to the size of the fixed bed. The accuracy of the approximation increases with a decreasing particle size.

We may also note something interesting. If we have small variations along the width and depth in a fixed bed reactor (or radius if it is a cylindrical reactor), we can describe the macroscopic model with a 1D model along the height of the reactor, from the inlet to the outlet. We obtain a model with two independent space variables, one in the z-direction and one for the porous catalyst particle radius, r. In the case of our microreactor above, such a simplification gives a decent agreement with the more detailed model for the average concentration along the height and for the total conversion of the reactants.

The figure below shows a case different from the one that we modeled above. Here, the reactor is in the meter scale and there are millions of catalyst particles in the fixed bed. The catalyst is less active than the cases we studied so far. The fixed bed reactor in this figure cannot be simplified with a 1D model, since the inlet nozzles (in red) influence the concentration distribution in the reactor. In this case, the model is 3D in the macroscale with an additional fourth dimension for the particle radius and a fifth independent variable for time.

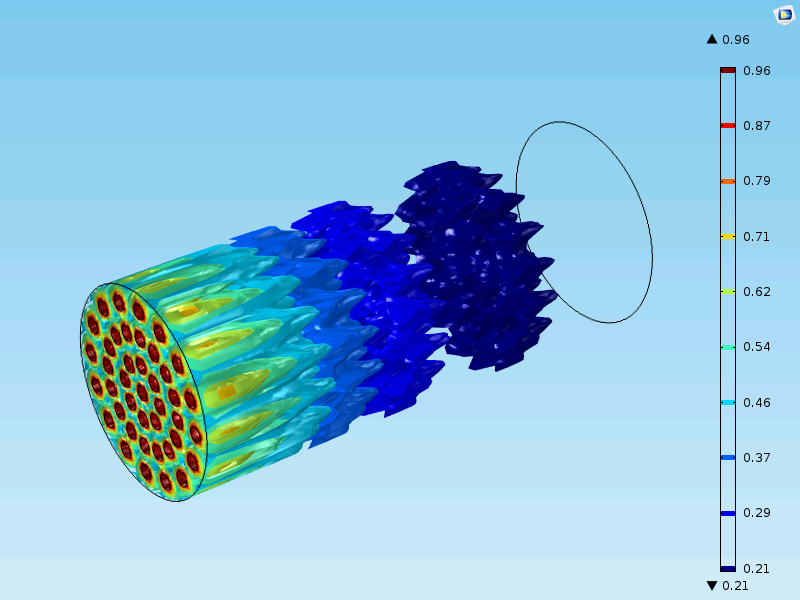
Concluding Remarks

We have seen that we may describe fairly complex catalytic geometric structures at the microscopic level including the transport, adsorption, reaction, and desorption steps.

This description was approximated at a microscopic level using homogenization, which depicts the catalyst particles as porous slabs.

In the next step, we used the simplified particle model to model a large number of particles, but then describing the position and shape of every particle in detail, only the internals of the particles were simplified.

Then, when the number of particles became too large as well, we also homogenized the fixed bed domain at the macroscopic reactor level.

By following the procedure of homogenization and approximation, from the microscopic particle level to the macroscopic reactor level, we can design the catalyst in detail and study the influence of this design on the total reactor performance. In addition, this methodology can also be used ”backwards”. In other words, we can study how the macroscopic operation may influence the operating conditions at the microscopic level, thus allowing us to adapt the catalyst and bed design for the relevant operating conditions at different positions in the reactor.