
A question that we are asked all of the time is if COMSOL Multiphysics can model laser-material interactions and heating. The answer, of course, depends on exactly what type of problem you want to solve, as different modeling techniques are appropriate for different problems. Today, we will discuss various approaches for simulating the heating of materials illuminated by laser light.
An Introduction to Modeling Laser-Material Interactions
While many different types of laser light sources exist, they are all quite similar in terms of their outputs. Laser light is very nearly single frequency (single wavelength) and coherent. Typically, the output of a laser is also focused into a narrow collimated beam. This collimated, coherent, and single frequency light source can be used as a very precise heat source in a wide range of applications, including cancer treatment, welding, annealing, material research, and semiconductor processing.
When laser light hits a solid material, part of the energy is absorbed, leading to localized heating. Liquids and gases (and plasmas), of course, can also be heated by lasers, but the heating of fluids almost always leads to significant convective effects. Within this blog post, we will neglect convection and concern ourselves only with the heating of solid materials.
Solid materials can be either partially transparent or completely opaque to light at the laser wavelength. Depending upon the degree of transparency, different approaches for modeling the laser heat source are appropriate. Additionally, we must concern ourselves with the relative scale as compared to the wavelength of light. If the laser is very tightly focused, then a different approach is needed compared to a relatively wide beam. If the material interacting with the beam has geometric features that are comparable to the wavelength, we must additionally consider exactly how the beam will interact with these small structures.
Before starting to model any laser-material interactions, you should first determine the optical properties of the material that you are modeling, both at the laser wavelength and in the infrared regime. You should also know the relative sizes of the objects you want to heat, as well as the laser wavelength and beam characteristics. This information will be useful in guiding you toward the appropriate approach for your modeling needs.
Surface Heat Sources
In cases where the material is opaque, or very nearly so, at the laser wavelength, it is appropriate to treat the laser as a surface heat source. This is most easily done with the Deposited Beam Power feature (shown below), which is available with the Heat Transfer Module as of COMSOL Multiphysics version 5.1. It is, however, also quite easy to manually set up such a surface heat load using only the COMSOL Multiphysics core package, as shown in the example here.
A surface heat source assumes that the energy in the beam is absorbed over a negligibly small distance into the material relative to the size of the object that is heated. The finite element mesh only needs to be fine enough to resolve the temperature fields as well as the laser spot size. The laser itself is not explicitly modeled, and it is assumed that the fraction of laser light that is reflected off the material is never reflected back. When using a surface heat load, you must manually account for the absorptivity of the material at the laser wavelength and scale the deposited beam power appropriately.
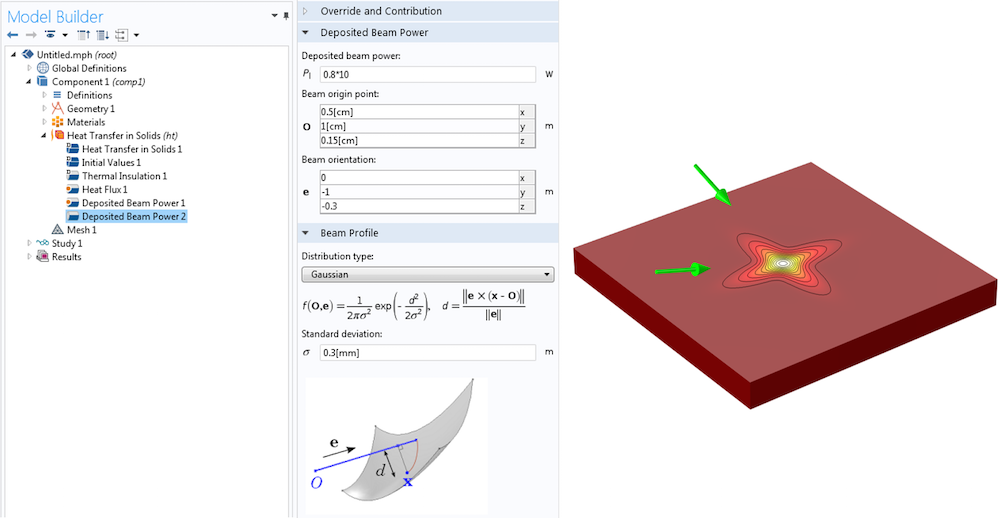
The Deposited Beam Power feature in the Heat Transfer Module is used to model two crossed laser beams. The resultant surface heat source is shown.
Volumetric Heat Sources
In cases where the material is partially transparent, the laser power will be deposited within the domain, rather than at the surface, and any of the different approaches may be appropriate based on the relative geometric sizes and the wavelength.
Ray Optics
If the heated objects are much larger than the wavelength, but the laser light itself is converging and diverging through a series of optical elements and is possibly reflected by mirrors, then the functionality in the Ray Optics Module is the best option. In this approach, light is treated as a ray that is traced through homogeneous, inhomogeneous, and lossy materials.
As the light passes through lossy materials (e.g., optical glasses) and strikes surfaces, some power deposition will heat up the material. The absorption within domains is modeled via a complex-valued refractive index. At surfaces, you can use a reflection or an absorption coefficient. Any of these properties can be temperature dependent. For those interested in using this approach, this tutorial model from our Application Gallery provides a great starting point.
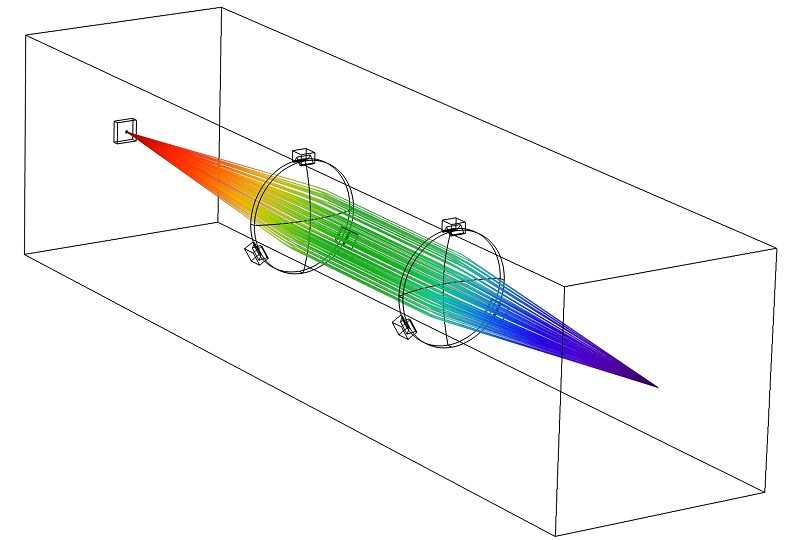
A laser beam focused through two lenses. The lenses heat up due to the high-intensity laser light, shifting the focal point.
Beer-Lambert Law
If the heated objects and the spot size of the laser are much larger than the wavelength, then it is appropriate to use the Beer-Lambert law to model the absorption of the light within the material. This approach assumes that the laser light beam is perfectly parallel and unidirectional.
When using the Beer-Lambert law approach, the absorption coefficient of the material and reflection at the material surface must be known. Both of these material properties can be functions of temperature. The appropriate way to set up such a model is described in our earlier blog entry “Modeling Laser-Material Interactions with the Beer-Lambert Law“.
You can use the Beer-Lambert law approach if you know the incident laser intensity and if there are no reflections of the light within the material or at the boundaries.
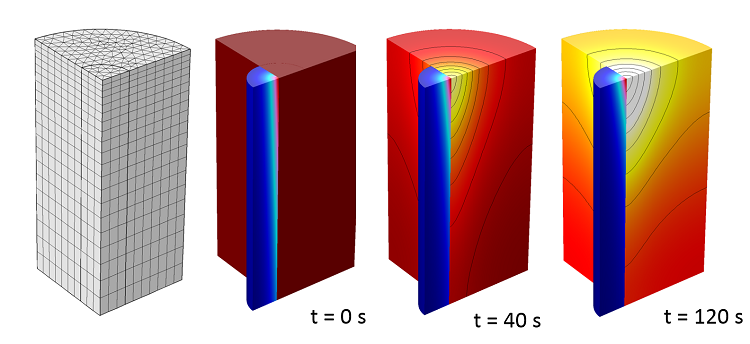
Laser heating of a semitransparent solid modeled with the Beer-Lambert law.
Beam Envelope Method
If the heated domain is large, but the laser beam is tightly focused within it, neither the ray optics nor the Beer-Lambert law modeling approach can accurately solve for the fields and losses near the focus. These techniques do not directly solve Maxwell’s equations, but instead treat light as rays. The beam envelope method, available within the Wave Optics Module, is the most appropriate choice in this case.
The beam envelope method solves the full Maxwell’s equations when the field envelope is slowly varying. The approach is appropriate if the wave vector is approximately known throughout the modeling domain and whenever you know approximately the direction in which light is traveling. This is the case when modeling a focused laser light as well as waveguide structures like a Mach-Zehnder modulator or a ring resonator. Since the beam direction is known, the finite element mesh can be very coarse in the propagation direction, thereby reducing computational costs.
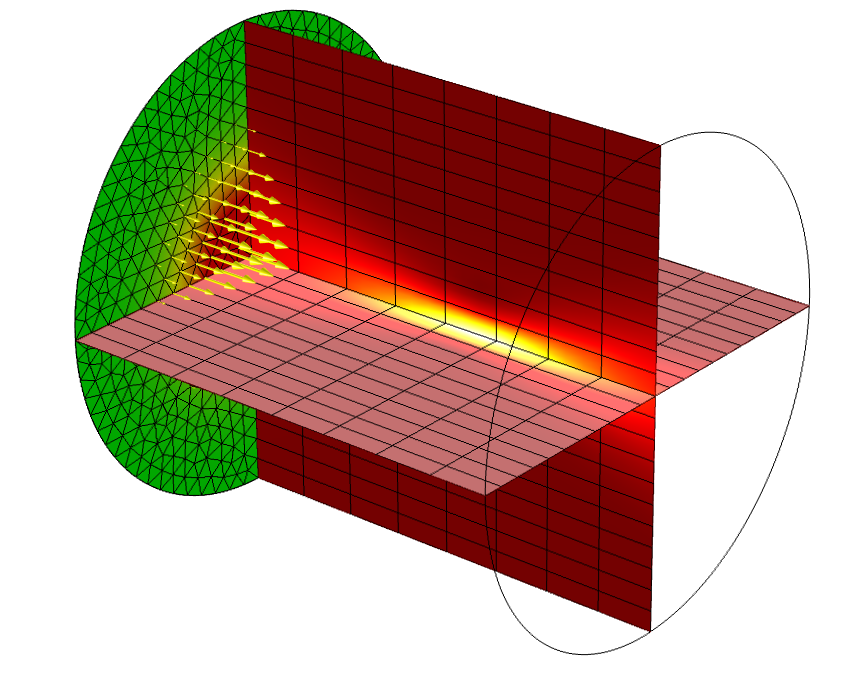
A laser beam focused in a cylindrical material domain. The intensity at the incident side and within the material are plotted, along with the mesh.
The beam envelope method can be combined with the Heat Transfer in Solids interface via the Electromagnetic Heat Source multiphysics couplings. These couplings are automatically set up when you add the Laser Heating interface under Add Physics.
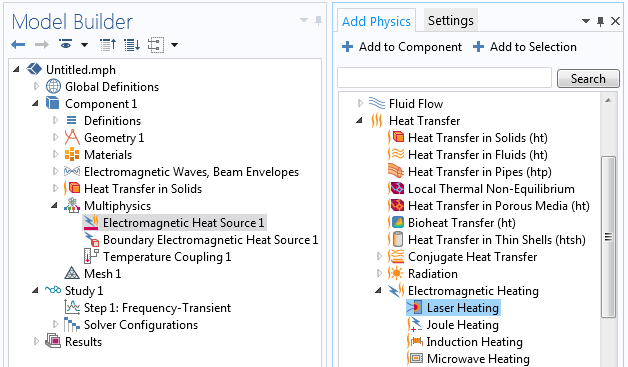
The Laser Heating interface adds the Beam Envelopes and the Heat Transfer in Solids interfaces and the multiphysics couplings between them.
Full Wave
Finally, if the heated structure has dimensions comparable to the wavelength, it is necessary to solve the full Maxwell’s equations without assuming any propagation direction of the laser light within the modeling space. Here, we need to use the Electromagnetic Waves, Frequency Domain interface, which is available in both the Wave Optics Module and the RF Module. Additionally, the RF Module offers a Microwave Heating interface (similar to the Laser Heating interface described above) and couples the Electromagnetic Waves, Frequency Domain interface to the Heat Transfer in Solids interface. Despite the nomenclature, the RF Module and the Microwave Heating interface are appropriate over a wide frequency band.
The full-wave approach requires a finite element mesh that is fine enough to resolve the wavelength of the laser light. Since the beam may scatter in all directions, the mesh must be reasonably uniform in size. A good example of using the Electromagnetic Waves, Frequency Domain interface: Modeling the losses in a gold nanosphere illuminated by a plane wave, as illustrated below.
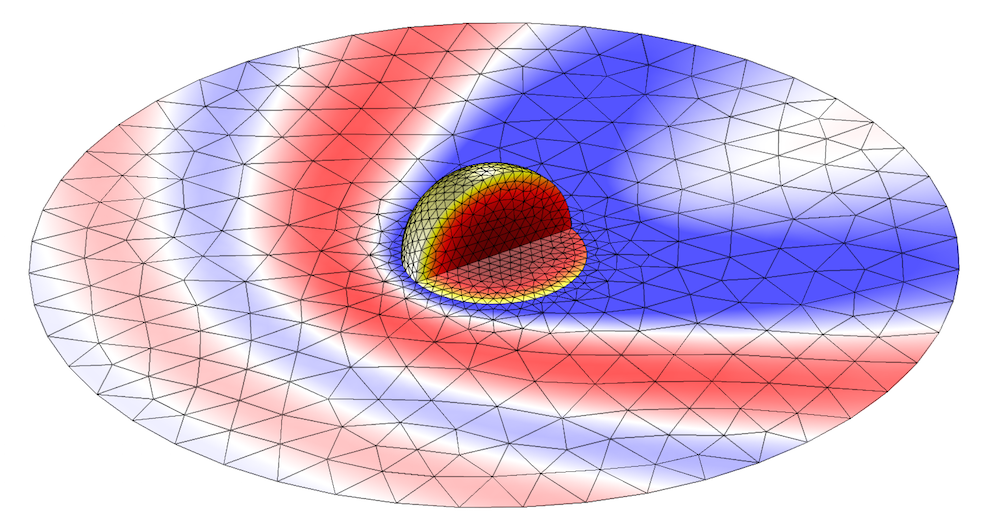
Laser light heating a gold nanosphere. The losses in the sphere and the surrounding electric field magnitude are plotted, along with the mesh.
Modeling Heat Transfer, Convection, and Reradiation Within and Around a Material
You can use any of the previous five approaches to model the power deposition from a laser source in a solid material. Modeling the temperature rise and heat flux within and around the material additionally requires the Heat Transfer in Solids interface. Available in the core COMSOL Multiphysics package, this interface is suitable for modeling heat transfer in solids and features fixed temperature, insulating, and heat flux boundary conditions. The interface also includes various boundary conditions for modeling convective heat transfer to the surrounding atmosphere or fluid, as well as modeling radiative cooling to ambient at a known temperature.
In some cases, you may expect that there is also a fluid that provides significant heating or cooling to the problem and cannot be approximated with a boundary condition. For this, you will want to explicitly model the fluid flow using the Heat Transfer Module or the CFD Module, which can solve for both the temperature and flow fields. Both modules can solve for laminar and turbulent fluid flow. The CFD Module, however, has certain additional turbulent flow modeling capabilities, which are described in detail in this previous blog post.
For instances where you are expecting significant radiation between the heated object and any surrounding objects at varying temperatures, the Heat Transfer Module has the additional ability to compute gray body radiative view factors and radiative heat transfer. This is demonstrated in our Rapid Thermal Annealing tutorial model. When you expect the temperature variations to be significant, you may also need to consider the wavelength-dependent surface emissivity.
If the materials under consideration are transparent to laser light, it is likely that they are also partially transparent to thermal (infrared-band) radiation. This infrared light will be neither coherent nor collimated, so we cannot use any of the above approaches to describe the reradiation within semitransparent media. Instead, we can use the radiation in participating media approach. This technique is suitable for modeling heat transfer within a material, where there is significant heat flux inside the material due to radiation. An example of this approach from our Application Gallery can be found here.
Summary
In this blog post, we have looked at the various modeling techniques available in the COMSOL Multiphysics environment for modeling the laser heating of a solid material. Surface heating and volumetric heating approaches are presented, along with a brief overview of the heat transfer modeling capabilities. Thus far, we have only considered the heating of a solid material that does not change phase. The heating of liquids and gases — and the modeling of phase change — will be covered in a future blog post. Stay tuned!






Comments (16)
ashkan razmara
September 7, 2015hello
I want to simulate phase change with laser heating over metal ( solid material ) to see how laser melt it. can you help me about that please.
regard
amir
Walter Frei
September 22, 2015Dear Amir,
This would be a question which would be appropriate to ask directly to your COMSOL Support Team.
Best,
Lyubo
July 13, 2020Mr Frei,
Which one is the best for Laser Ablation?
OLUWASEUN ADEYEMI
August 29, 2017I want to model Laser cutting and Laser drilling using COMSOL Multiphysics can you please help me on the step by step approach of the Simulation.
Caty Fairclough
September 11, 2017Hi Oluwaseun,
Thanks for your comment.
For questions related to your modeling, please contact our Support team.
Online Support Center: https://www.comsol.com/support
Email: support@comsol.com
zoubir bekkari
October 27, 2017I want to model Laser cutting and Laser drilling using COMSOL
mona aghaee
January 29, 2018Hi,
I have problem modeling radiation heat transfer in a slab. A constant radiation hits an slab and part of that is transferred through the slab, part is absorbed within the slab and part is reflected. How should I model this? I already know the absorptance, reflectance and transmittance of the slab. Please advise.
Thanks
Mona
Tran Hung
March 8, 2018Hi all,
Now I’m modeling the nano pulsed laser heating a nano-object to predict the temperature of the object and the air around it. I have some questions:
1. How can I describe the laser beam as Gaussian beam in Electromagnetic Waves, Frequency domain? (The wavelength is 1064nm and the spot size is 20 um).
2. Which field should I use for the simulation, the scattered field has Gaussian beam background wave type or full-field? With the full-field, now I don’t know how to put the laser beam into the model.
3. Is the Microwave heating physic suitable for use in this case?
Please help me or recommend the related topic!
Thank you!
Rishabh Bhatia
June 18, 2018I need help in designing the optical cable with a nanoparticle attached at its one end and study the effect of passing a laser through it. Is there any procedure to follow to accomplish this?
I was thinking of drawing two separate geometries:-
1- A spherical nanoparticle
2- An optical fiber cable
Then I can attach the two models together.
Can anyone guide me through the procedure to follow for it?
adried Allemand
February 11, 2022The question is quite simple , in RF (frequency domain) we can find , A(ω), R(ω) , Τ(ω) : absorption ,refrection and transimition as a function of frequency. In general this problem can be solved in a lot and different geometries using ports. Imagine I excite a laser beam in frequency domain, I solve the problem for all frequencies of interest, can I get with an inverse Fourier Transform ( FREQUENY TO TIME ) the Reflectivity as a function of time or/and space?
Walter Frei
February 11, 2022 COMSOL EmployeeHello adried, Note that you can also solve a time-domain model, as in: https://www.comsol.com/model/time-to-frequency-fft-analysis-of-a-distributed-bragg-reflector-89811
Alp Aydin
March 7, 2022Do you have example for top-hat square model?
Walter Frei
March 7, 2022 COMSOL EmployeeHello Alp,
If you’re referring to the beam profile, I’d suggest looking over the Radiative Beam in Absorbing Media interface. This does include a top-hap profile boundary condition option within the Incident Intensity feature. Happy modeling!
Alison Felix
September 28, 2022Hello Walter,
Is there a blog entry or tutorial model for the beam envelope method? I’m trying to obtain an output very similar to the one illustrated in this post but I can’t get the Laser Heating coupling quite right. It would be very helpful if there was an example in similar description format as the one using the Beer-Lambert Law.
Walter Frei
September 29, 2022 COMSOL EmployeeHello Alison,
A good example to build upon is:
https://www.comsol.com/model/self-focusing-14639
You could simply add heat transfer in solids, and then use the laser-heating multiphysics coupling.
Especially since this domain is of a homogeneous material illuminated by a steady beam, and would not have features sizes comparable to the phonon and IR wavelengths nor short-time duration phenomena that might motivate a more complex thermal model, such as a Cattaneo-type equation . But, f you want some inspiration for such cases, see: https://www.comsol.com/blogs/hydrodynamic-thermal-transport-in-the-kinetic-collective-model/
Happy Modeling!
The Linh Pham
August 17, 2023Hello,
I’m trying to reproduce my experiment in COMSOL. I have metamaterial sample (with periodicity of 5 micrometers), and the sample size is 1×1 mm^2. I used CW laser source and measure the transmission and reflection. Can I also simulate the impact of heating, and the expansion and compression of the microstructure over time? I think the dynamics should be in picosecond time scale.
Best,
Linh