
Today, guest blogger Björn Fallqvist of Lightness by Design, a COMSOL Certified Consultant, discusses using simulation to provide insight into the mechanical behavior of cells.
Biological cells are essential for life as we know it. They not only store and replicate hereditary information in the form of DNA but also are instrumental in biological processes. In most, if not all, of these processes, the mechanical behavior of cells is a main factor in ensuring normal physiological functions.
The Importance of Biological Cells
It goes without saying that we would not exist or function without cells. Vertebrates utilize the circulation of red blood cells, erythrocytes, to deliver oxygen to body tissue. Fibroblasts use their contractile machinery to migrate to — and start the healing process of — wounds. The endothelial cells lining our blood vessels serve as filtration barriers. These cells not only rely on biochemical/transport mechanisms but also on their mechanical behavior to ensure normal physiological functions.
The structural entity responsible for providing cellular stiffness is an interconnected network known as the cytoskeleton, visualized in the image below. This cytoskeleton primarily consists of three types of polymerized filaments, each with their own distinct structure and mechanical characteristics:
- Actin
- Intermediate filaments
- Microtubules
This complex foundation provides cells with the ability to adapt their mechanical properties to the environment, both instantaneously and over time.
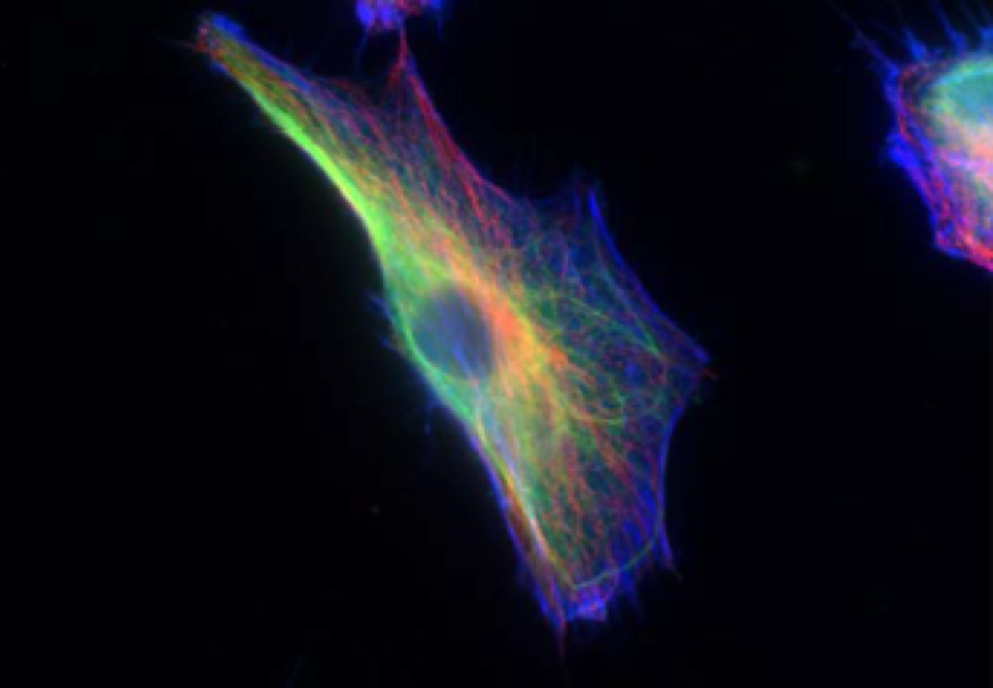
A fibroblast cell with the cytoskeleton visualized, including actin (blue), intermediate filaments (green), and microtubules (red). Used with permission from Rathje et al. from the paper “Oncogenes induce a vimentin filament collapse mediated by hdac6 that is linked to cell stiffness”.
Both cells and cytoskeletal networks are highly viscoelastic, as you can see in the plot below of a relaxation curve from a cell indentation experiment by atomic force microscopy (AFM).
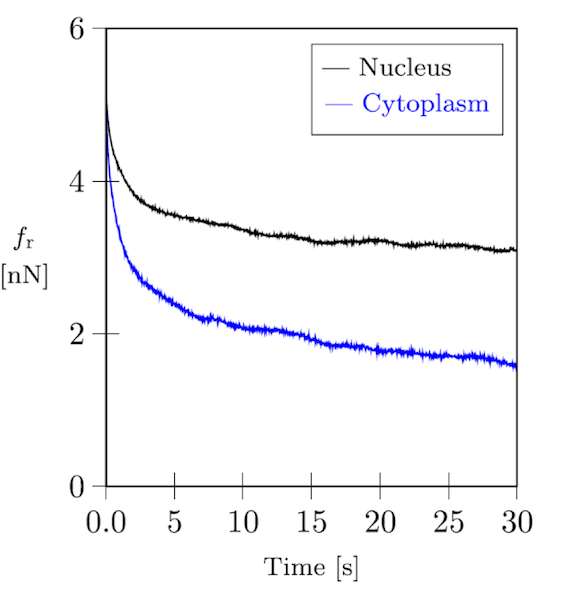
Force relaxation curve of a fibroblast cell.
Numerous examples exist in which a diseased cell exhibits abnormal mechanical properties, promoting the progression of pathology. The cytoskeleton found in these cells is often found to behave differently compared to healthy cells. For example, cancer cells are known to exhibit significant stiffness variations compared to control cells. In many cases, this can be linked to the cytoskeleton. The intermediate filament network could be collapsing around the nucleus or there could be increased cell spreading (closely linked to the actin cytoskeleton through focal adhesions).
Investigating the Mechanical Behavior of Filaments and Cells
As mentioned, the cytoskeleton is a dynamic entity with the capability of remodeling itself on a time scale from milliseconds to hours. A consequence of this is a pronounced viscoelastic behavior, due to the nature of the constituent networks. For example, a solution of actin filaments behaves like a solid at short time scales and a liquid at longer time scales. This is due to the link between the thermal fluctuations of semiflexible filaments and their propensity to slide between each other; i.e., they are more or less kinematically constrained at short time scales. The temperature is also an important factor, partly because it affects the thermal behavior, but also because of various linking proteins in the solution.
Taken together, the mechanical behavior of this type of underlying polymer network, together with other cell constituents (e.g., cell nucleus and membrane), it is clear that a detailed analysis accounting for all of these factors is nearly impossible. However, it is possible to circumvent this challenge and obtain results by considering the cell at a macroscopic level.
By creating a finite element model in the COMSOL Multiphysics® software, you can essentially ignore the heterogeneous intracellular structure and instead view it as a continuum; i.e., the displacement field is continuous. This is an acceptable approximation if your goal is to quantify the macroscopic cell response to external stimuli.
The computational model described in this blog post is that of a relaxation test. A rigid indenter is pressed into the soft, viscoelastic cell, and the resulting relaxation of the indentation force is measured and compared to experimental data.
Computational Model of a Cell
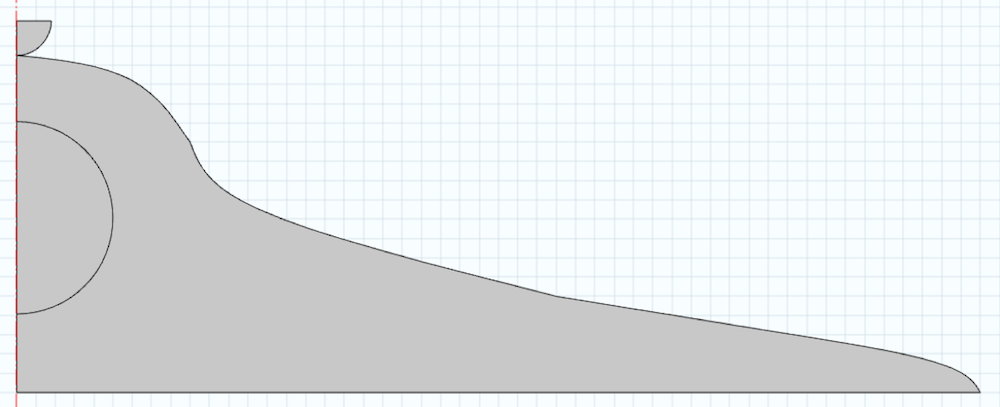
A model of a cell with typical dimensions is seen below. Note that the domain is created around the centerline. The semicircular section is the cell nucleus, which will also influence the mechanical response. We also create an indenter in the geometry and neglect the cell membrane in this analysis. For simplicity, we perform a 2D analysis by assuming the cell is axisymmetric.
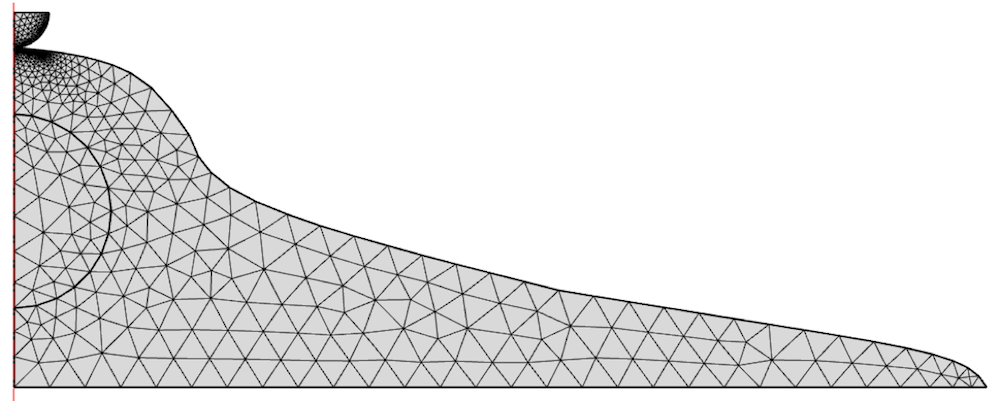
The model is meshed with 2D elements and refined under the indenter.
The choice of material model for the cell cytoplasm and nucleus should reflect both the instantaneous and long-term response of the material. A linear elastic model is far too simple, as cells can typically withstand large strains and exhibit significant strain hardening. For the cytoplasmic response, we can choose a simple hyperelastic material model, the neo-Hookean model, in which stresses and strains are computed from a strain energy density function Ψ on the form
In this form, where the material is assumed (nearly) incompressible, the shear modulus µ, elastic volume ratio Jel, bulk modulus κ, and isochoric first invariant \overline{I}_1 are included. To incorporate the viscoelastic behavior, two generalized Maxwell branches are also included. The nucleus has been found to be mainly elastic and is therefore modeled without viscoelastic branches.
The chosen material parameters are shown in this table:
| Domain | Shear Modulus | Bulk Modulus | Energy Factor 1 | Relaxation Time 1 | Energy Factor 2 | Relaxation Time 2 |
|---|---|---|---|---|---|---|
| Nucleus | 1.667 kPa | 5000 kPa | N/A | N/A | N/A | N/A |
| Cytoplasm | 0.155 kPa | 1000 kPa | 10 | 0.5 s | 10 | 50 s |
The bottom of the cell is constrained vertically. While in reality, the cell adheres to the substrate through focal adhesions, this should be a local effect and not significantly influence the force response.
Contact between the indenter and the cell is enforced by a penalty formulation, using the indenter as the source boundary. The indenter domain is prescribed a velocity of 0.1 µm/s, until the total vertical displacement is 4.6 µm. It is subsequently held fixed for the remainder of the analysis, up to a total time of 30 s.
Simulation Results
The local deformation of the cell after indentation is shown in the plot below.
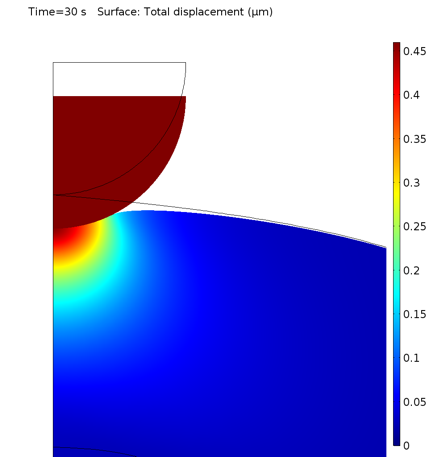
Deformation of the cell under the indenter.
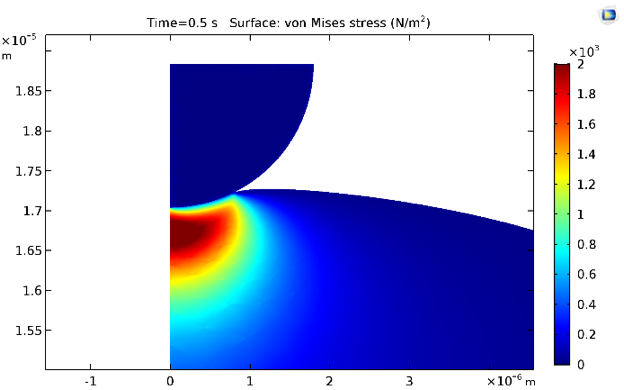
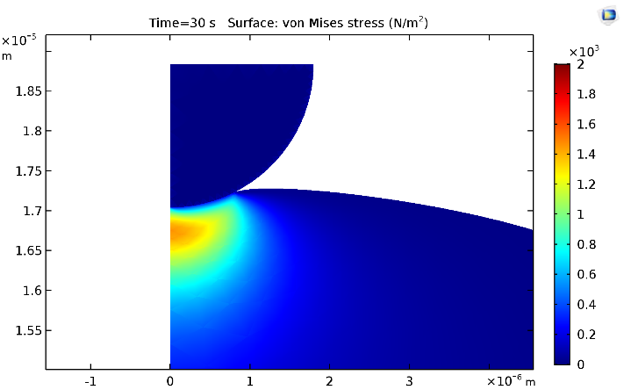
The equivalent von Mises stresses at times 0.5 s and 30 s are shown below. Naturally, the stresses decrease due to stress relaxation because of the inclusion of viscoelastic branches for the cytoplasmic material model.
Stress distribution at 0.5 s (left) and 30 s (right).
The vertical reaction force on the indenter can be extracted from COMSOL Multiphysics and compared with experimental data.
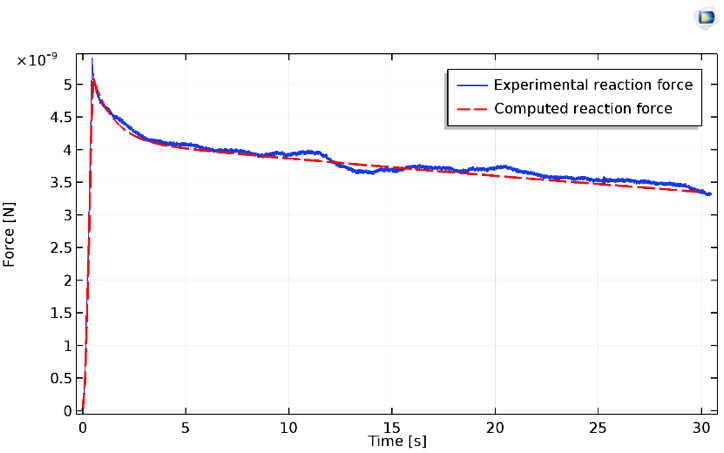
Results for the indentation force of the cell, both experimental (blue) and computed (red).
The relaxation, as measured by experiments, typically exhibits at least two distinct regimes. These values are reasonably well predicted by the simple neo-Hookean model, along with its two viscoelastic branches. It should be noted that the initial indentation regime exhibits severe strain hardening prior to the constant slope (apparent in the plot above).
Final Thoughts on Biomechanical Modeling
As discussed, COMSOL Multiphysics can be easily used to replicate the viscoelastic behavior of cells by (comparatively) simple material models. Naturally, an increasing level of complexity can be obtained by using more complicated material models. In this case, using other hyperelastic models, such as the Mooney-Rivlin or Ogden models, in combination with a greater number of viscoelastic branches may yield even more accurate results. Keep in mind that as more material parameters are needed, more experimental data points must be available for the material in question.
The cell is in reality a far more complex system than modeled here. There is a constant exchange of mechanical and biochemical signals that constantly alter the intracellular structure, cell shape, and locomotion behavior. Suffice to say, modeling the cell as a continuum is a major simplification, but such an approximation can serve us well in many cases. If we were to analyze metastasizing cells, for example, it may be enough to characterize their macroscopic stiffness in order to assess their capability to squeeze through tissue or arteries. In such a case, the stiffness of the cell as a whole in comparison to the obstacle would be the determining factor, not the detailed interactions of, say, the cytoskeleton and cell nucleus.
It should also be mentioned that the cell is not only a complex system but also far from deterministic and not uniquely characterized by a set of geometrical and material parameters. The response between individual cells varies depending on their health, state of locomotion, and cell cycle state, among other factors. To properly assess the mechanical cell response of a cell type experimentally, a greater number of individual cells would need to be probed. However, we are content with evaluating the capability of modeling the response of an individual cell.
In general, not only cells but also other biological materials can often be modeled by utilizing hyperelastic material models. Depending on the particular material and time scale, viscoelastic behavior can also be included. This opens up some interesting opportunities in the field of biomechanical modeling.
For example, a common type of cardiovascular condition is atherosclerosis in which white blood cells accumulate on the arterial wall, reducing blood flow and increasing the risk of a heart attack due to a blood clot. A common procedure to alleviate this condition is angioplasty, when a balloon is inserted into the artery and inflated. A mechanical stent is then often used to stabilize the artery section. Using COMSOL Multiphysics, we could capture the hyperelastic-viscoelastic behavior of the arterial wall, as well as composite characteristics due to collagen fiber directions, and compute the instantaneous and transient development of stresses and strains.
Editor’s note, 8/20/18: The corresponding cell relaxation model file has been added to the Application Exchange. You can find it here.
About the Author
Björn Fallqvist is a consultant at Lightness by Design working with product development based on numerical analysis. He obtained a PhD from the Royal Institute of Technology in 2016, working with developing constitutive models to capture the mechanical behavior of biological cells. His main professional interest and specialization is in the fields of material characterization and using various material models to capture physical phenomena.
References
- Rathje et al, “Oncogenes induce a vimentin filament collapse mediated by hdac6 that is linked to cell stiffness”, Proceedings of the National Academy of Sciences, 111, pp. 1515–1520, 2014.
- B. Fallqvist et al., “Experimental and computational assessment of F-actin influence in regulating cellular stiffness and relaxation behaviour of fibroblasts”, Journal of the Mechanical Behavior of Biomedical Materials, Vol 59, pp. 168–184, 2016.




Comments (24)
Maohua Lin
January 14, 2018can i get this comsol file? mlin2014@fau.edu
Thanks,
Gizem Aydemir
May 8, 2018Can I get this Comsol file?
aydemir.gizem@outlook.com
Thanks..
CHUKWUEMEKA ANI
June 29, 2018Please can i get the Comsol file on this model
My email is: cjani@wpi.edu
Hirohito Yamazaki
August 6, 2018Can I get this COMSOL file? This is similar to what I am trying to do. I tried to make the model by referring to your paper.
My email: h.yamazaki@northeastern.edu
Tong Ling
August 16, 2018Can I get the COMSOL file for this model? We’re studying cellular dynamics and would try to make a model by referring to your paper.
My email is: tongling@stanford.edu
Thanks!
Sugriva Raiford
November 10, 2018Hi,
Would you please explain about why did you use the order 4 integral of Lagrange multiplier for displacement to calculate the force rate?
Björn Fallqvist
November 15, 2018Hi,
Using the lagrange multiplier as a weak constraint is just another means of calculating the reaction force of the indenter (see “Computing accurate fluxes” in the Comsol Multiphysics Reference Manual). I was originally intending to create an optimization loop for the material parameters with regards to experimental data, and to perform gradient-based optimization, the post-variable reaction force cannot be used, but lagrage-multiplier variables can.
Ryan Greenhalgh
May 17, 2019Please can I get the Comsol file on this model
My email is: rdg31@cam.ac.uk
pawan tiwari
June 3, 2019I would appreciate a demo of your comsol cell model
pawan tiwari
June 3, 2019I would appreciate a comsol file at pawan.ktiwari@gmail.com
Björn Fallqvist
June 4, 2019Ryan and Pawan, the link to the file is included in the blog post itself.
Best regards Björn
pawan tiwari
June 4, 2019Dear Bjorn Fallqvist,
I downloaded the mph file (Experimental comparison_relaxation_base), however, unable to run and visualize the results.
Do you have an instruction manual to draw and run the model step-wise.
Thank you very much
With regards
Pawan
fedaoui kamel
July 19, 2019Please can I get the Comsol file on this model
My email is: kamel.fedaoui@umc.edu.dz
Björn Fallqvist
August 12, 2019Dear Pawan, it appears that the COMSOL file specified in the blog is corrupt. I have provided a new file to COMSOL which I hope will be available soon.
Best regards
Björn
EL HAFI TARIK
May 23, 2020I would appreciate a demo of your comsol cell model.
Please can I get the Comsol file on this model
My email is: tarik.elhafi@gmail.com
Thanks
Cho youngheun
October 3, 2019Please can I get the Comsol file on this model
My email is: dudgms123@naver.com
Thanks..
Brianne Christopher
November 12, 2019 COMSOL EmployeeHi Cho,
You can download the MPH-file featured in this blog post via the Application Exchange link: https://www.comsol.com/community/exchange/631/
EL HAFI TARIK
May 23, 2020I would appreciate a demo of your comsol cell model.
Please can I get the Comsol file on this model
My email is: tarik.elhafi@gmail.com
Thanks
Seyedeh Golsa Ghetmiri
July 7, 2020I’d appreciate it if you can email me the COMSOL file.
Email: golsa.ghetmiri@gmail.com
Nurzhanna Bakuova
July 10, 2021I would appreciate a demo of your comsol cell model.
Please can I get the Comsol file on this model
My email is: 2610301b@student.gla.ac.uk
Thanks
amin sha'bani
November 13, 2022can i get this comsol file?
amin.shabani.elec92@gmail.com
Thanks.
SEYHAN OKUYAN AKCAN
December 25, 2022Please can i get the Comsol file on this model
My email is: seyhan.okuyan@boun.edu.tr
Fedai Inanir
May 24, 2023can Iget this comsol file?
inanir@yildiz.edu.tr
I am appreciated in advanced
Thank you so much.
xiao bai
May 13, 2024I would appreciate a demo of your comsol cell model.
Please can I get the Comsol file on this model
My email is: xiaoxiaobai830@gmail.com
Thanks