All posts by Temesgen Kindo

Exploiting Maximum Principles to Save Time and Resources
By exploiting maximum principles in large and complex models, you will save time and computational resources without having to buy a bigger computer or leave your model to solve overnight.
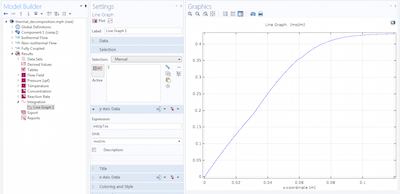
Integrals with Moving Limits and Solving Integro-Differential Equations
Learn how to analyze spatial integrals over variable limits, whether they are prescribed explicitly or defined implicitly. (Part 2 of 2)
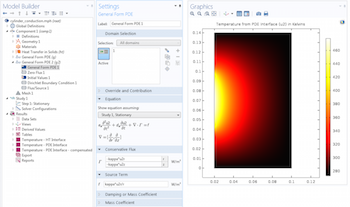
Guidelines for Equation-Based Modeling in Axisymmetric Components
Here’s your comprehensive guide to equation-based modeling for problems with cylindrical coordinates and axisymmetric components.
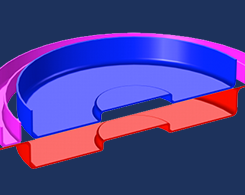
How to Reuse a Deformed Shape as a Geometry Input
Let’s say you deform a shape in your model (say, by applying a mechanical load to a thin piece of metal) and want to use this deformed object as part of a new geometry construction. How?

How to Integrate External Data Files with Your COMSOL® App
Have you ever wanted to integrate your simulation apps, built with the Application Builder in COMSOL Multiphysics®, with external data files? In this blog post, we show you how…
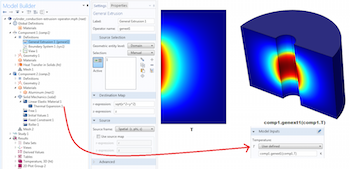
Part 2: Mapping Variables with General Extrusion Operators
Learn how to use the General Extrusion operators, which are designed to handle nonlinear mappings and the mapping of variables between geometric entities of different dimensions. Part 2 of 2.
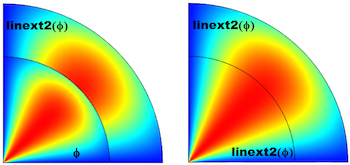
Accessing Nonlocal Variables with Linear Extrusion Operators
In some modeling scenarios, you may need to transfer variables from one region of a computational domain (the source) to another (the destination). This can be done with an extrusion operator.
Verify Simulations with the Method of Manufactured Solutions
The Method of Manufactured Solutions involves assuming a solution, obtaining source terms, solving the problem, and comparing the results with the assumed solution. Use it to verify your models.
