All posts by Walter Frei

Implementing a Simple Temperature Controller with a Component Coupling
Learn how to implement a simple temperature controller (a feedback loop) in a thermal process simulation in COMSOL Multiphysics®. We demonstrate with a silicon wafer example >>

Computing and Controlling the Volume of a Cavity
See a method for modeling enclosed volumes containing incompressible fluids (under the additional assumption that the momentum and energy transfer via the fluid is small) in COMSOL Multiphysics®.
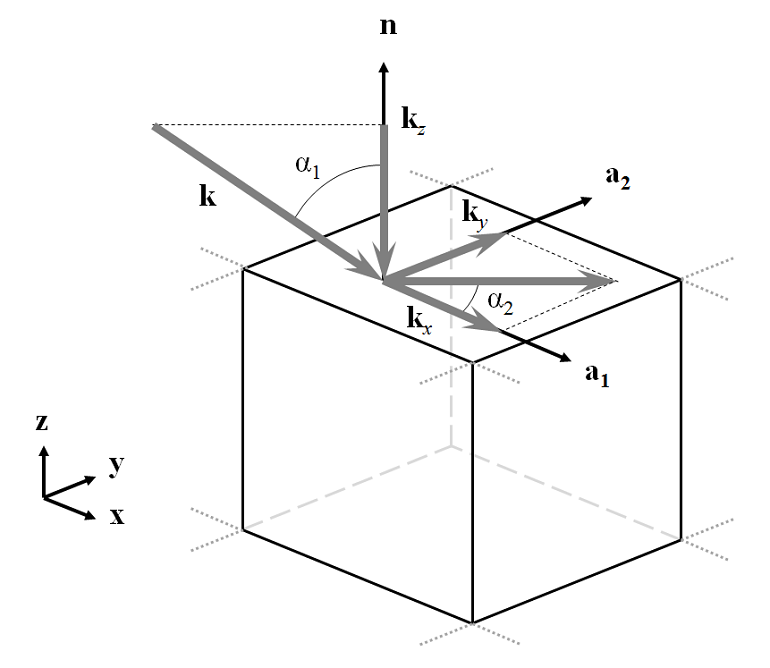
Modeling Electromagnetic Waves and Periodic Structures
Oftentimes, it is of interest to model an EM wave (light, microwaves) incident upon periodic structures, such as diffraction gratings, metamaterials, and frequency selective surfaces.
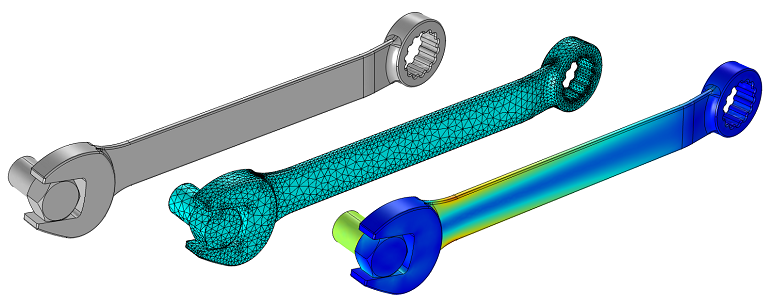
Parameterizing the Dimensions of Imported CAD Files
Learn how to modify an imported geometry with some clever usage of the Deformed Geometry interface in COMSOL Multiphysics®.

Using Adaptive Meshing for Local Solution Improvement
One of the perennial questions in finite element modeling is how to choose a mesh. We want a fine enough mesh to give accurate answers, but not too fine, as that would lead to an impractical solution time. As we’ve discussed previously, adaptive mesh refinement lets the software improve the mesh, and by default it will minimize the overall error in the model. However, we often are only interested in accurate results over some subset of the entire model space. […]
Learning to Solve Multiphysics Problems Effectively
One of the questions we get asked often is how to learn to solve multiphysics problems effectively. Over the last several weeks, I’ve been writing a series of blog posts addressing the core functionality of the COMSOL Multiphysics software. These posts are designed to give you an understanding of the key concepts behind developing accurate multiphysics models efficiently. Today, I’ll review the series as a whole.
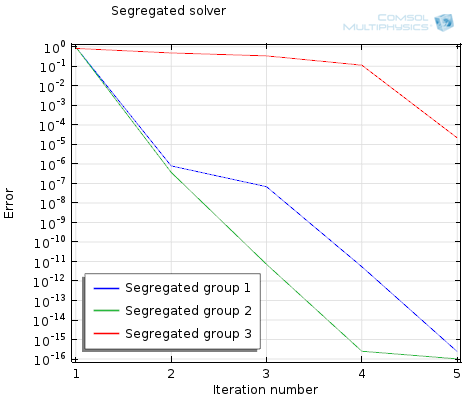
Improving Convergence of Multiphysics Problems
In our previous blog entry, we introduced the Fully Coupled and the Segregated algorithms used for solving steady-state multiphysics problems in COMSOL. Here, we will examine techniques for accelerating the convergence of these two methods.
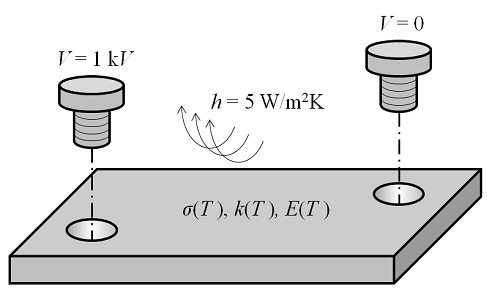
Solving Multiphysics Problems
Here we introduce the two classes of algorithms used to solve multiphysics finite element problems in COMSOL Multiphysics. So far, we’ve learned how to mesh and solve linear and nonlinear single-physics finite element problems, but have not yet considered what happens when there are multiple different interdependent physics being solved within the same domain.



