
Have you ever wondered why boaters wear polarized sunglasses? It’s because sunlight reflecting off the water is primarily polarized in one direction, and polarized sunglasses will block this component of the reflected light, thus reducing glare. To understand why this is, we can use COMSOL software. This example solves the governing Maxwell’s equations using the RF Module or Wave Optics Module to simulate light incident at an angle upon a dielectric medium, and the solution shows agreement with analytic solutions.
When Light Hits a Dielectric Medium
Sunlight is essentially incoherent light; it is composed of many wavelengths and varying polarizations. However, we can assume linearity of the electromagnetic fields, so any polarization of light can be treated as the sum of two orthogonal polarizations — one that has the electric field polarized parallel to the plane of the interface, and the other that has the magnetic field parallel to the plane of the interface.
When a ray of light (an electromagnetic wave) propagating through free space hits a dielectric medium, part of the light will be transmitted and part will be reflected. The fraction of the light that is reflected or transmitted is dependent upon the angle of incidence, the permittivity of the dielectric, and the polarization. This can also be described by the Fresnel equations, which are an analytic solution to Maxwell’s equations.
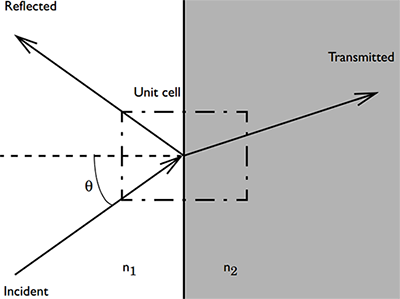
Schematic showing light incident upon a dielectric interface. The angle of incidence is denoted by θ. Part of the light will be transmitted and part will be reflected.
Instead of solving the Fresnel equations, we can build a COMSOL model to simulate an infinite plane wave of light incident upon a dielectric medium. Using either the RF Module or the Wave Optics Module, we can build a unit cell describing a small region around the dielectric interface. We solve the full Maxwell’s equations in the unit cell, with periodic boundary conditions and ports to truncate the modeling domain.
Fresnel Equations and COMSOL Model Results Agree
Let’s take a look at the results of our benchmark model, which solves for two orthogonal polarizations of light and computes the reflection and transmission coefficients with respect to incident angle.

The electric field in the y-direction (surface slice plot) and the power flow (arrow plot).
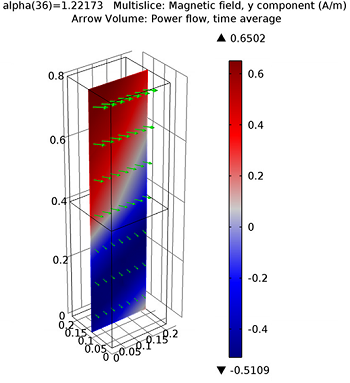
The magnetic field in the y-direction and the power flow. Both are shown for θ = 70°.
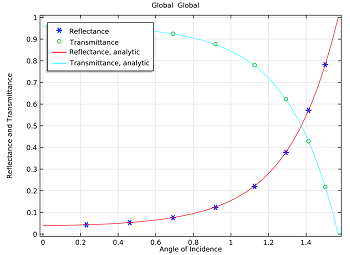
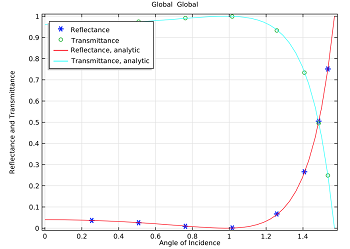
Comparing COMSOL model results with analytic solution for reflectance and transmittance for electric field incidence (left) and magnetic field incidence (right).
As you can see in the above plots, the benchmark model results agree with the analytic solution. We can also see that different polarizations of light will reflect differently off of an air-dielectric interface, and this tells us why polarized sunglasses are popular with boaters!



Comments (1)
Maturi Renuka
July 6, 2018How to match the phase of the reflected and transmitted wave with analytical formulas?