
The electron energy distribution function (EEDF) plays an important role in plasma modeling. Various approaches can be used to describe the EEDF, such as using an analytic function like a Maxwellian or Druyvesteyn function or solving the Boltzmann equation. Today, we will demonstrate the influence that the EEDF has on a plasma model’s results.
Editor’s note: This blog post was updated on July 5, 2024. It now includes links to related supplementary materials and the proof-of-concept model.
Electron Energy Distribution Function (EEDF)
The electron energy distribution function is essential in plasma modeling because it is needed to compute electron source terms and transport parameters from appropriate cross sections for electron impact collisions. By default, the Plasma interface uses a Maxwellian EEDF. This is a good start to prepare a model and obtain general tendencies (e.g., electron density vs. applied voltage). However, for more detailed studies, a computed EEDF should be used because for most cold plasma applications, the EEDF is strongly in nonequilibrium. In other words, the EEDF deviates considerably from a Maxwellian distribution. In the following sections, we show several options to use for analyzing the EEDF and its influence in the results of a model of a DBD reactor.
Describing the EEDF
To describe the EEDF, several possibilities are available, such as a Maxwell or Druyvesteyn function. In addition, a generalized form is available, which is an intermediate between the Maxwell and the Druyvesteyn function.
Functions That Describe the EEDF
| Maxwell |
f(\epsilon)=\varphi^{-3/2}\beta_1\exp\left(-\frac{\epsilon\beta_2}{\varphi}\right)
\beta_1=\Gamma(5/2)^{3/2}\Gamma(3/2)^{-5/2},\ \beta_2=\Gamma(5/2)\Gamma(3/2)^{-1}
|
| Druyvesteyn |
f(\epsilon)=\varphi^{-3/2}\beta_1\exp\left(-\left(\frac{\epsilon\beta_2}{\varphi}\right)^2\right)
\beta_1=\Gamma(5/4)^{3/2}\Gamma(3/4)^{-5/2},\ \beta_2=\Gamma(5/4)\Gamma(3/4)^{-1}
|
| Generalized |
f(\epsilon)=\varphi^{-3/2}\beta_1\exp\left(-\left(\frac{\epsilon\beta_2}{\varphi}\right)^g\right)
\beta_1=\Gamma(5/2g)^{3/2}\Gamma(3/2g)^{-5/2},\ \beta_2=\Gamma(5/2g)\Gamma(3/2g)^{-1}
|
Here, ϵ is the electron energy, (eV); \varphi is the mean electron energy, (eV); and g is a factor between 1 and 2.
For a Maxwell distribution function, g is equal to 1, while g equals 2 for a Druyvesteyn distribution. Lastly, \Gamma is the incomplete Gamma function.
The distribution functions assume that elastic collisions dominate, thus the effect of inelastic collisions (e.g., excitation or ionization) on the distribution function is insignificant. In such a case, the distribution function becomes spherically symmetric. In elastic collisions with neutral atoms, the electrons’ direction of motion is changed, but not their energies (due to the large mass difference).
Maxwellian Function
If the electrons are in thermodynamic equilibrium among each other, the distribution function is Maxwellian. However, this is only true if the ionization degree is high. Here, electron-electron collisions drive the distribution toward a Maxwellian shape. The figures below show Maxwellian EEDFs represented in two different forms.
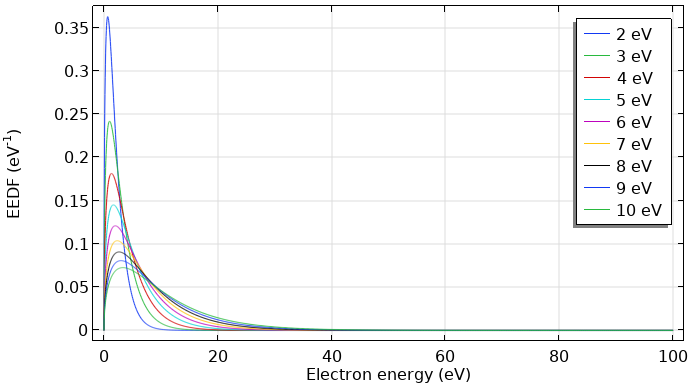
Maxwellian EEDF in eV–1 for mean electron energies from 2–10 eV.
Normally, the distribution function is divided by \sqrt{\epsilon}. This kind of distribution function is also known as an electron energy probability function (EEPF). For a Maxwellian function, this results in a straight line with a slope of (-1/k_B T), as shown below.
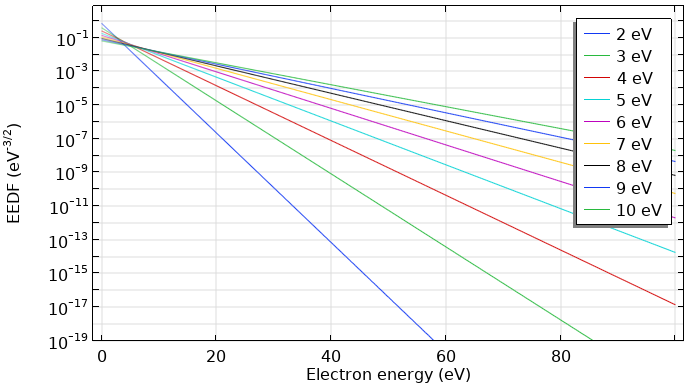
Maxwellian EEDF in eV–3/2 for mean electron energies from 2–10 eV.
Druyvesteyn Function
Instead of using a constant collision frequency, like in the Maxwellian EEDF, the Druyvesteyn EEDF assumes a constant, electron-energy-independent cross section. This leads to a drop of the EEDF at higher electron energies for the same mean electron energy.
The Boltzmann Equation
Furthermore, the EEDF can be computed by solving the Boltzmann equation. The Boltzmann equation describes the evolution of the distribution function, f, in a six-dimensional phase space:
To solve the electron Boltzmann equation in a reasonable time, and therefore compute the EEDF, drastic simplifications are necessary. A common approach is to expand the distribution function in spherical harmonics. The EEDF is assumed to be almost spherically symmetric, so the series can be truncated after the second term (a so-called two-term approximation). This approach is used in the Boltzmann Equation, Two-Term Approximation interface.
From the above-mentioned distribution functions, this approach is the most accurate way to compute the EEDF because an anisotropic perturbation is introduced. Another point that makes this approach more accurate is that, commonly, the EEDF is computed based on provided coherent sets of electron impact cross sections that describe how electrons lose/gain energy in collisions with the background gas. This way, the EEDF describes how electrons gain energy from the electric field and lose it in collisions for a specific gas or mixture of gases.
Comparing the Maxwell, Druyvesteyn, and Computed Distribution Functions
As shown below, the computed EEDF strongly deviates from a Maxwellian EEDF. The main difference is that the high-energy tail drops considerably when the electrons reach energies of the first electronic excited state of argon at 11.5 eV. The computed EEDF is also underpopulated at low energies and overpopulated in the mid energies, giving a slower slope in the region before the first excitation level. This EEDF shape is commonly obtained in low-temperature plasmas of noble gases.
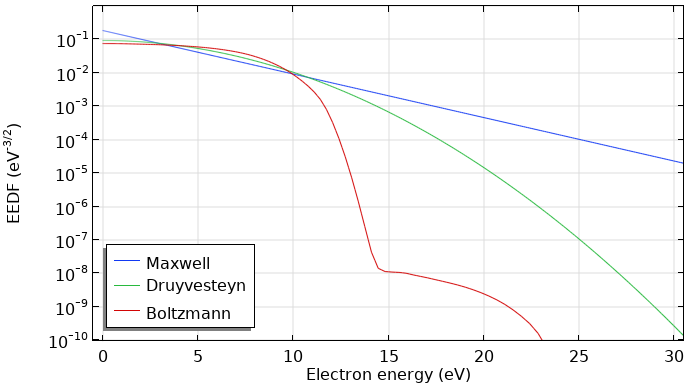
Comparison of a Maxwell, Druyvesteyn, and computed EEDF using the Boltzmann Equation, Two-Term Approximation interface for argon. All EEDFs have a mean electron energy of 5 eV.
Rate Coefficients and Transport Parameters
In the plasma model, the EEDF is needed to compute the rate coefficients, k_k, for the electron collisions reactions, according to the equation:
In the above equation, \gamma = \sqrt{2q/m_e}, the electron energy is ϵ, and \sigma_k is the cross section for reaction, k.
The rate coefficients for excitation and ionization highly depend on the shape of the EEDF. This is mainly due to the fast drop-off in the population of electrons at energies exceeding the first excitation level threshold. Using a Maxwellian EEDF can lead to an overestimation of the ionization rate, which is shown below.
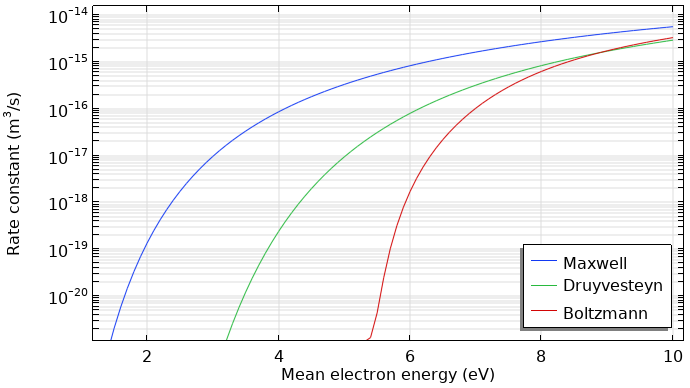
Rate coefficients for argon ionization computed with different kinds of EEDFs.
Furthermore, the electron transport properties can be computed by means of the EEDF, using the Boltzmann Equation, Two-Term Approximation interface. The computed transport coefficients have less dependence on the type of EEDF.
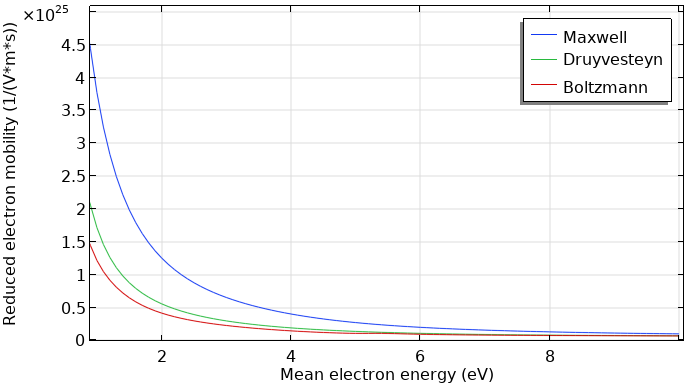
Reduced electron mobility computed with different kinds of EEDFs.
Comparing the Model Results of a Dielectric Barrier Discharge
Although the rate coefficients can differ by orders of magnitude, we must be aware that tendencies of macroscopic and averaged quantities do not change that drastically when changing the EEDF. In the Application Gallery, there is a model of dielectric barrier discharge (DBD). This model simulates electrical breakdown in atmospheric pressure argon.
For demonstration purposes, the model mentioned above was recomputed using the three different kinds of EEDFs. If you are interested in reviewing details of how the EEDF can be obtained from the Boltzmann Equation, Two-Term Approximation interface and then used in the Plasma interface, please check out this blog post. The key step is consecutive export/import of the EEDF function and other relevant properties, such as reduced electron mobility. You can also download the modified up-to-date file using the button at the end of this blog post.
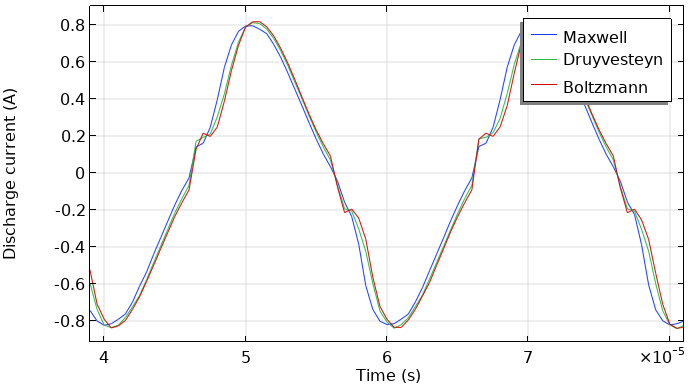
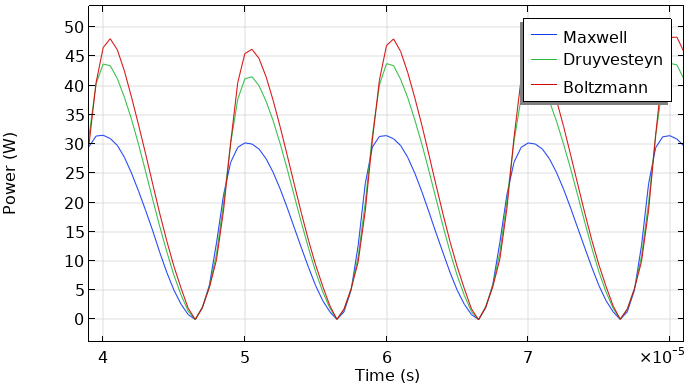
Here the focus is on the obtained results. The next two figures show the total current at the grounded electrode and the instantaneously absorbed power in the plasma. The plasma is driven with a sinusoidal voltage with a frequency of 50 kHz. The figures show the behavior over two periods. The results look similar. So, the choice of the EEDF influences the modeling results, not orders of magnitude (but in this case, much less than a factor of two). This, of course, depends on the model and the specific results you wish to extract.
Total discharge current in the DBD vs. time (left). Absorbed power of the DBD vs. time (right).
Next Step
Try out the model discussed in this blog post by clicking the button below, which will take you to the Application Gallery:
Further Learning
- Read more about the interface on the COMSOL Blog:
- Explore another model using the Boltzmann equation:
- Check out this Learning Center course devoted to plasma modeling:


Comments (2)
Mark Baldry
March 17, 2020Thanks for this blog. Please elaborate on the quantitative difference between high and low degree of ionisation in terms of choosing between the Maxwellian and Druyvesteyn EEDF.
khalid hussain
September 6, 2022hi, I am Khalid I want to talk to you I am also PhD scholar in electrical engineering
so please send me your email so that I can talk you related to my study