
Space frames have been used as the foundation for the construction of many modern buildings, from the Louvre in France to Globen in Sweden. When designing space frames, we need to asses the risk of instability.
A Design Element in Modern Building Construction
With its notable display of historical artwork, the Louvre has become a central landmark in Paris, France. As the Louvre grew in popularity — eventually ranking as one of the world’s most visited museums — it became evident that the building’s original entrance could no longer handle the large number of guests admitted on a daily basis. The need for an entrance with a greater capacity prompted the construction of the Louvre Pyramid within the museum’s courtyard in 1989. This structure now serves as the main entrance to the building, descending visitors into a spacious lobby and then moving them up to the museum level.

The Louvre Pyramid. (“Courtyard of the Louvre Museum, with the Pyramid” by Alvesgaspar — Own work. Licensed under Creative Commons Attribution Share-Alike 3.0, via Wikimedia Commons).
In comparison to the Louvre’s classical architecture, the pyramid was based on a more modern design approach — the space frame. A space frame is a truss-like structure composed of interlocking struts that form a geometric pattern. Requiring few interior supports, these structures offer a lightweight and elegant solution in structural engineering. Additionally, due to their inherent rigidity, space frames are able to span large areas while maintaining a strong resistance.
The Louvre pyramid is just one example of a building based on a space frame design. Many other structures, such as the Eden Project in England and Globen in Sweden, have also used a space frame as the basis for their construction. With its common application in modern buildings, it is important to study how loads affect the stability of such structures.
Applying Loads to Space Frames
In the new COMSOL Multiphysics version 5.0 model, Instability of a Space Arc Frame, we set up and analyze a space frame. In this benchmark model, the frame undergoes concentrated loading at various points, with a small lateral load implemented to break the structure’s symmetry. The description of the space frame and the applied loads are based on the example from “A Mixed Co-rotational 3D Beam Element for Arbitrarily Large Rotations” by Z.X. Li and L. Vu-Quoc.
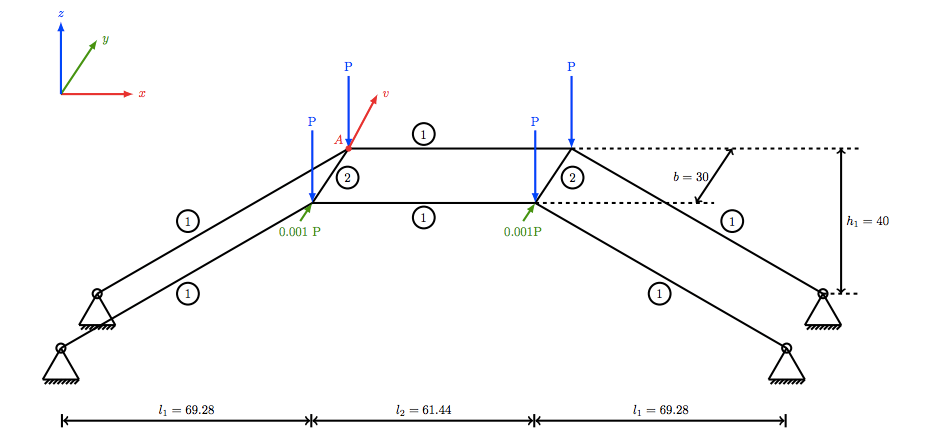
A schematic depicting the space frame’s geometry.
As a constraint, all of the frame’s base points are pinned. Vertical concentrated loads P are applied to the top four corners of the space frame. Meanwhile, lateral loads of 0.001*P are applied to the frame’s two front corners. These lateral loads are designed to perturb the frame’s symmetry to implement a controlled instability. The figure below shows the final state of the deformed frame.
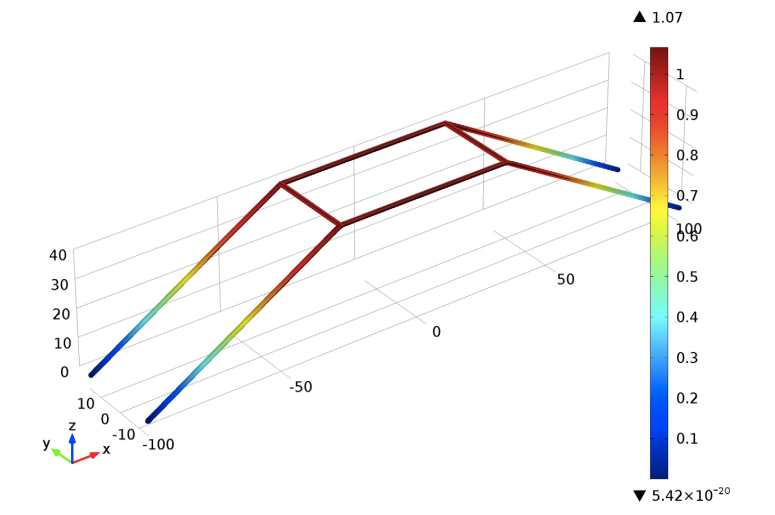
Deformed space frame.
Next, we can evaluate the relationship between the compressive load and the horizontal displacement on point A of the frame. Comparing the reference data with the simulation results, the plot below illustrates a strong agreement between the two findings.
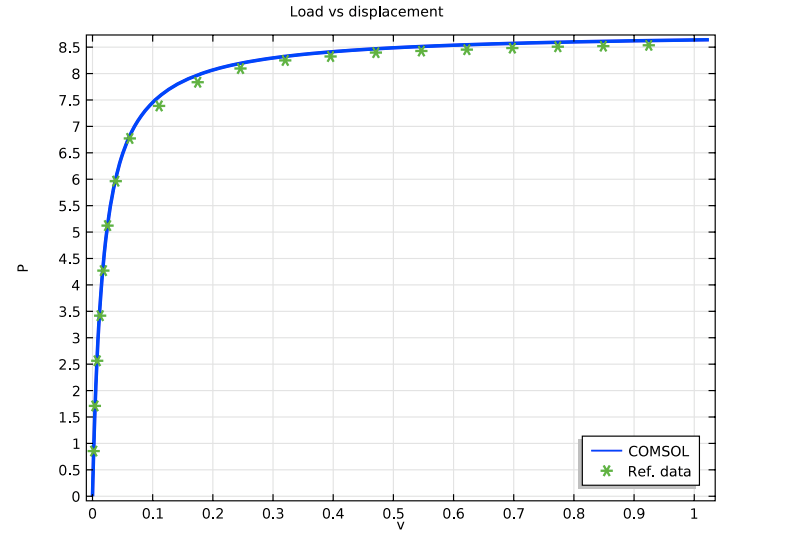
A plot relating load parameter P and displacement v. Here, the simulation results are compared with the reference data.
Furthermore, this plot highlights an instability occurring at a parameter value of around 8.0, even though a deviation from linearity can be seen much earlier. In practice, an imperfect structure’s critical load is often far lower than that of the ideal structure, as was discussed in this previous blog post.
Try It Yourself
- Download the model: Instability of a Space Arc Frame




Comments (0)