
When solving a chemical species transport problem, we are often dealing with cases that have a high Péclet number, where the ratio of the advection to diffusion is very high. We may also be dealing with such problems in structures that are periodic along the flow direction, and where the flow field itself is periodic. Using COMSOL Multiphysics, we can greatly reduce our computational requirements for such problems by using General Extrusion component couplings and the Previous Solution operator.
This is the second blog post in a two-part series. Read Part 1 here.
Multiphysics Modeling of a Microfluidic Device with Periodicity
I recently wrote a blog post about exploiting periodicity to reuse the flow solution in the modeling of a microfluidic device. To quickly refresh our memories, a microfluidic device may feature small serpentine channels, as shown in the image below. Two inlets introduce different solutes in the same solvent, and good mixing at the outlet is desired.

A typical microfluidic device. Image by IX-factory STK — Own work. Licensed under CC BY-SA 3.0, via Wikimedia Commons.
We know that it is possible to compute the fluid flow field in only one of the repeating unit cells, and to pattern this flow solution along the repeating structure to define the flow field along the entire device. The Transport of Diluted Species problem can then be solved in the repeated section, as shown in the figure below.
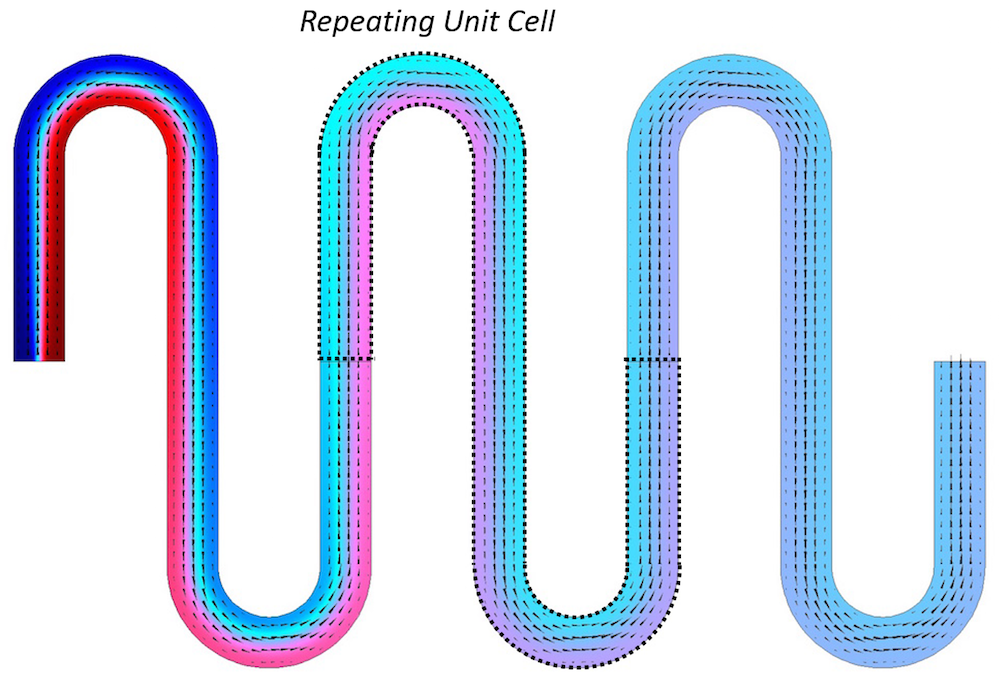
One approach is to compute the flow field on one unit subcell. This flow solution can be used by the chemical species transport problem, solved over the entire domain.
Shortly after finishing my earlier blog post on this topic, one of my colleagues challenged me to come up with an even simpler way of modeling the same situation, which made me think of the following problem.
It may not be immediately obvious from the above image that this case has a very high Péclet number, meaning that the transport of the species due to the motion of the fluid is far greater than the transport via species, via diffusion. Stated another way, the solution downstream does not affect the solution upstream.
Now, if the Péclet number is high, then we do not necessarily need to solve the Transport of Diluted Species problem on the entire domain. We can solve it on the same unit cell used to compute the fluid flow field, but we need to come up with a way to map the species distribution at the output boundary back to the input boundary and rerun the simulation. Let’s find out how to do this.
General Extrusion Operators, Boundary Equations, Previous Solutions, and Parametric Sweeps
The modeling procedure we should follow is sketched out in the figure below. We can reduce our entire modeling domain down to one unit cell. We will compute the flow field in this unit cell using laminar inflow and outflow conditions. This computed flow field will be used as the transport term in the Transport of Diluted Species interface, which additionally requires a concentration profile at the inlet.
We can start by assuming a particular species concentration at the inlet and solve for the concentration field throughout the modeling domain. Then, we evaluate the concentration profile at the outlet; map that profile back to the inlet boundary, where it can be applied as a new inlet condition; and solve the model again. Each time we repeat this process, we are essentially solving for the concentration profile in the next (downstream) unit cell of our microfluidic device.
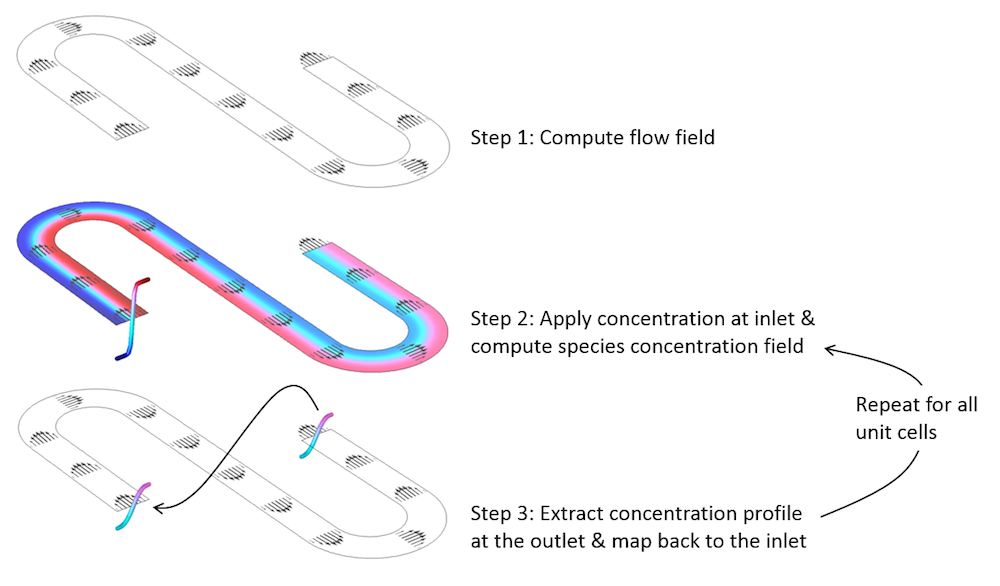
The solution procedure for modeling a repeated microfluidic device with a single unit cell.
The modeling implementation begins with a General Extrusion component coupling, named genext1, defined at the outlet boundary. This coupling simply maps the fields at the outlet boundary back to the inlet boundary by specifying a displacement along the x-axis, similar to the method shown in an earlier blog post.
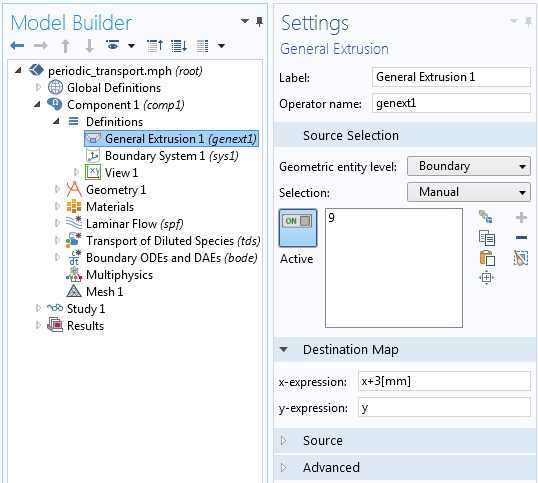
The General Extrusion component coupling maps the solution on one boundary to another boundary by the specified offset of 3 mm.
Next, a Boundary ODEs and DAEs interface is added to the inlet boundary. The settings for this interface are shown below. The variable is named c_b and the discretization is set to Lagrange — Linear to match the discretization of the Transport of Diluted Species interface. The Source Term for the Distributed ODE is (c_b-genext1(c))[m^3/mol], which sets the value of c_b at the inlet equal to c. The species concentration is computed at the outlet, which is mapped back to the inlet via the General Extrusion operator.
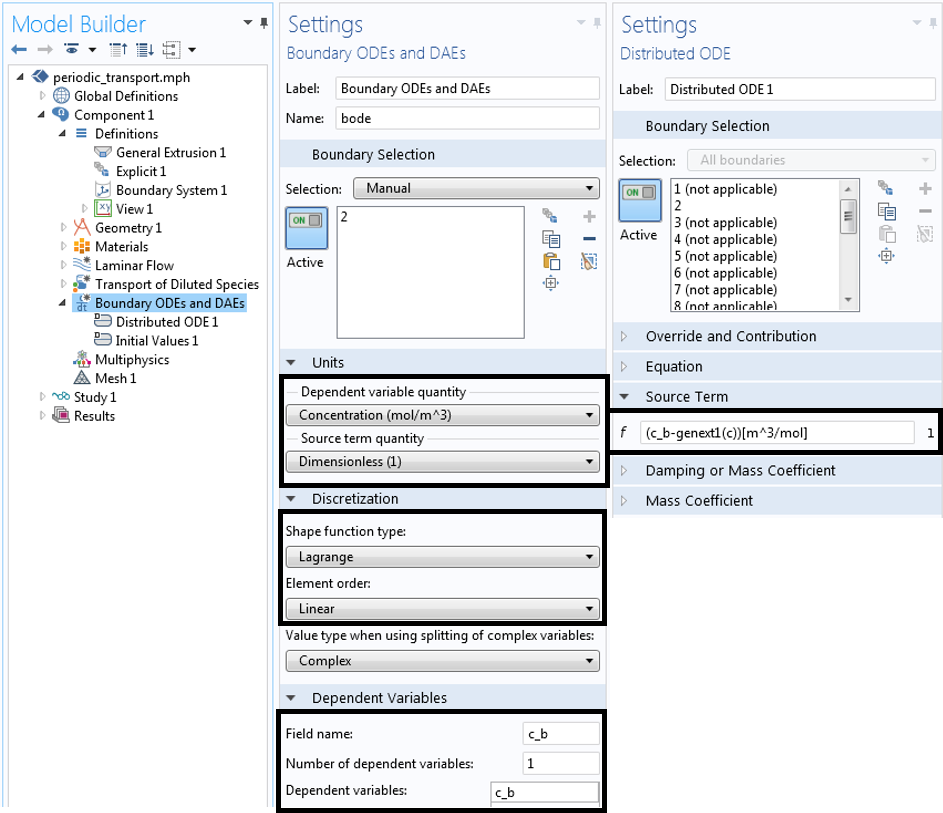
The Boundary ODEs and DAEs interface. Relevant settings are highlighted.
Next, let’s look at where the variable c_b is used. The screenshot below shows the Inflow boundary condition for the Transport of Diluted Species interface.
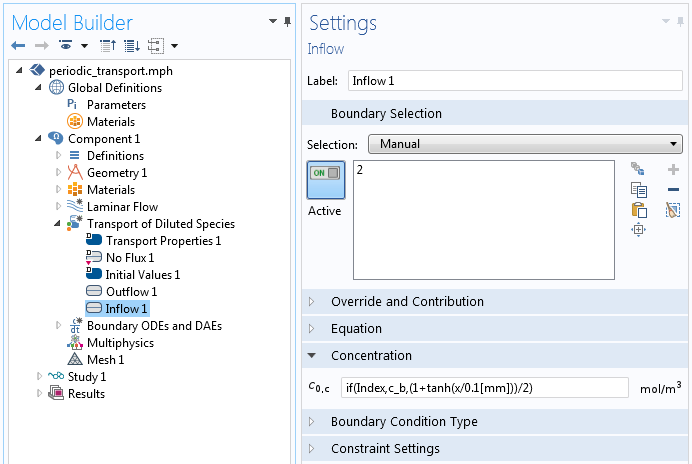
The inlet condition for the Transport of Diluted Species interface.
The expression entered into this field is if(Index,c_b,(1+tanh(x/0.1[mm]))/2), which uses the if() statement to set up a different inlet concentration based upon a Global Parameter, Index. The expression (1+tanh(x/0.1[mm]))/2 is the assumed species concentration at the inlet of the device (this concentration is arbitrarily set to range from zero to one) and is only applied if Index is equal to zero. For any other values of Index, the species concentration at the inlet is actually taken from the computed species concentration at the outlet.
But how do we specify that we want the previously computed outlet concentration to be used as the inlet concentration? For that, we need to modify our Study settings. The Study is composed of two sequential Stationary Steps. The first step solves the Laminar Flow interface alone. The resulting steady-state fluid velocity field is automatically passed along to the second step, which solves for both the Transport of Diluted Species and Boundary ODEs and DAEs interfaces.
The second Stationary Step includes an Auxiliary Sweep, as shown in the screenshot below. Note that the Index parameter is swept over the values 0, 1, and 2, which represent the three-unit cells of the system that we want to model. Also note that Run continuation for is set to No parameter (since there is no benefit of using load ramping or nonlinearity ramping in this case) and that Reuse solution for previous step is set to Yes.
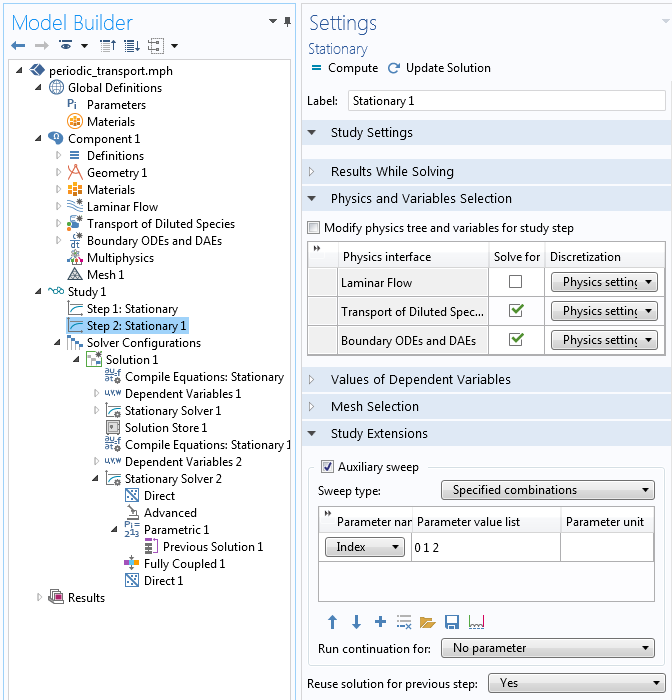
The Stationary study step with the Auxiliary sweep enabled.
There is one more modification that needs to be made to the Solver Configurations. We need to manually add a Previous Solution node to the Parametric node and specify that the variable c_b should be accessed at the previous step in the parameter sweep. The settings are shown below.
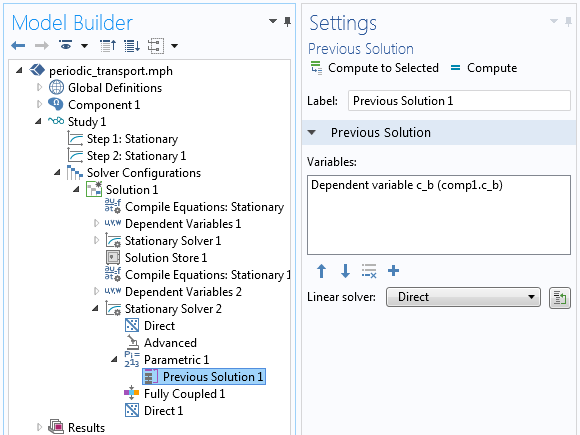
The Previous Solution node settings.
With these study settings, we repeat the simulation for each one of the three unit cells, passing the concentration field from the outlet back to the inlet before computing the concentration field. The results can be combined into a single plot showing the concentration profile throughout the entire domain of interest.
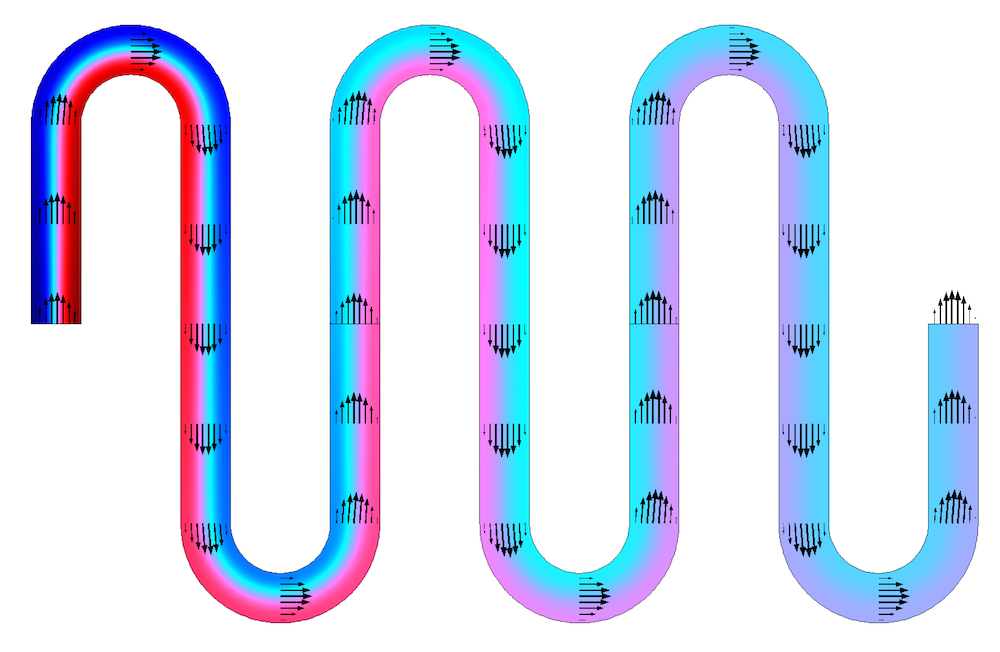
The concentration solution plotted for three unit cells, solved sequentially.
Summarizing Remarks on Modeling Periodic Structures with High Péclet Numbers
The approach shown in this blog post is valid for models of chemical species transport in periodic structures where the Péclet number is high. The process is certainly valid for solving other transport-dominant problems in COMSOL Multiphysics as well. Even though we assume here that the flow is periodic and the properties of the fluid are invariant, this approach can be extended to mapping the flow field from the outlet back to the inlet.
The problem shown here could also be addressed via LiveLink™ for MATLAB®, which provides us with a scripting interface that allows us to extract data, remap it, and rerun solutions with different inputs. Still, it is nice to see that we can build such models in the graphical user interface (GUI) as well.
The computational advantage here will grow with the number of unit cells that we have to analyze. If there are N unit cells, the memory requirements and the solution times for using this approach will be approximately N times smaller than building an entire model.
If you have questions about this, and are interested in using COMSOL Multiphysics for your modeling needs, please contact us.







Comments (5)
Jan Jäger
July 6, 2017Hey,
I tried this on my unit cell and it worked instantly (!). Nice tutorial. Just had to replace the (1+tanh(x/0.1[mm]))/2) term with my c_in.
“The results can be combined into a single plot showing the concentration profile throughout the entire domain of interest.”
How do you do this? I can’t figure out how to get the different indexes alligned in a 2D Array.
Walter Frei
July 7, 2017 COMSOL EmployeeHello Jan,
What you can do is make several different plots within a single plot group, and add a “Deformation” subfeature to move them to different locations.
Jan-Willem H
February 2, 2021Hi Walter,
It’s been a while since the most recent activity on this blog but I had a question with regard to simulating a unit cell.
I came across the following issues:
– In my simulation, I’ve employed a periodic flow condition to a channel with obstructions. However when doing so, the concentration profile at the outlet does no longer match the concentration at the inlet of the next unit cell
– When employing a mass flux at one of the walls, the introduced inflow concentration profile; (1+tanh(x/0.1[mm]))/2) does not enter the simulation (i.e. the inlet concentration profile is automatically zero)
Do you have any clue what might cause these problems?
Kind regards,
Jan-Willem
Jay Chou
October 24, 2022Dear Walter,
Very impressive and useful! May I ask a question?
Your case is a stationary problem. I am doing a similar study, but the transport process is non-steady. In this situation, can I still use this periodic method to simulate?
Hope to have your answer and help.
Thanks very much!
Jay Chou
洪博 郑
October 8, 2023Hello, Professor Walter Frei! I have achieved good results in my research using the method mentioned above. However, I’m wondering how to simultaneously extend the periodicity of both concentration and velocity variables. I would greatly appreciate it if you could provide some insights on this!