Hyperthermia oncology studies the biological effects of heat in the treatment of cancer. The goal is to propose noninvasive therapies, relying on devices such as thin microwave antennas or radio-frequency probes, inserted directly in the tumor through the skin of the patient. The numerical simulation of thermal damage due to electromagnetic heating of the biological tissue helps to optimize the clinical setup. Let’s see how to model this process with the COMSOL Multiphysics® software.
Hyperthermia Treatments for Cancer Therapy
In hyperthermia therapies, the power and spatial position of the electromagnetic heat source device should be adjusted depending on blood perfusion and the thermal and electrical properties of the healthy and necrosed tissues, in order to completely remove the tumor cells without damaging the surrounding tissue. The optimization of the clinical setup relies on a good understanding of the physical phenomena involved in the process.
Take the example of a hepatic tumor ablation using radiofrequency heating. The probe, made of a trocar and four electrode arms, is inserted into the tumor. An electric current passes through the probe and creates an electric field in the tissue, resulting in a heat source due to resistive heating. The trocar is electrically insulated, so the heat source is located in the immediate vicinity of the electrode arms. Heat is transferred by conduction around the electrodes, and within the limited volume, where the temperature stays above 45°C to 50°C for a certain period of time, the tumorous cells are damaged.
The image below shows the numerical prediction of thermal damage (green volume) by solving for the electric potential and temperature distributions in a schematic representation of a liver as a cylinder. A T = 37°C condition is applied on the outer boundary of the cylinder and on the thin vertical cylinder standing for a blood vessel. An electric potential of 22 V is imposed on the electrode surfaces.
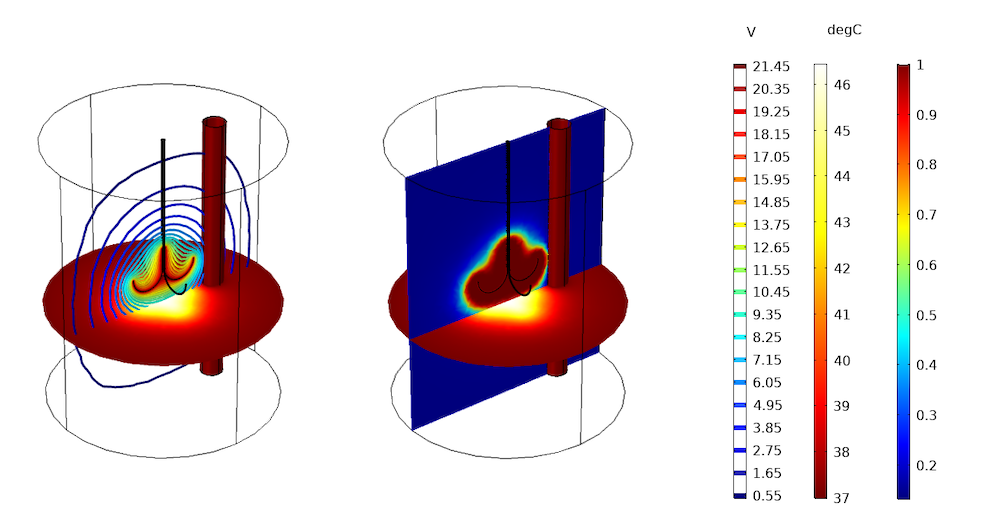
Numerical prediction of damage in liver tissue: contour plot of electrical potential distribution and slice plots of temperature distribution and fraction of damage after 10 minutes.
The transient analysis involves the Bioheat Transfer interface, the Electric Currents interface, and the Electromagnetic Heating multiphysics coupling. Transposed to a patient-specific geometry, in which the tumor is surrounded by the hepatic blood vessels and arteries, a similar multiphysics approach helps to optimize the probe position and power input for tissue damage conditions, despite the cooling provided by the surroundings.
The key concepts for modeling radiofrequency tissue ablation can be found in a previous blog post, with details about the modeling of the electric field in particular.
As another example, let’s consider microwave coagulation therapy, in which a thin microwave antenna operating at 2.45 GHz is inserted in the tumor. The device is made of a thin coaxial cable with a ring-shaped slot cut on the outer conductor and short-circuited at the tip. A plastic catheter surrounds the antenna. The image below shows the numerical prediction of damage by taking advantage of the rotational symmetry of the model (with the antenna represented at the left of the computational 2D domain).
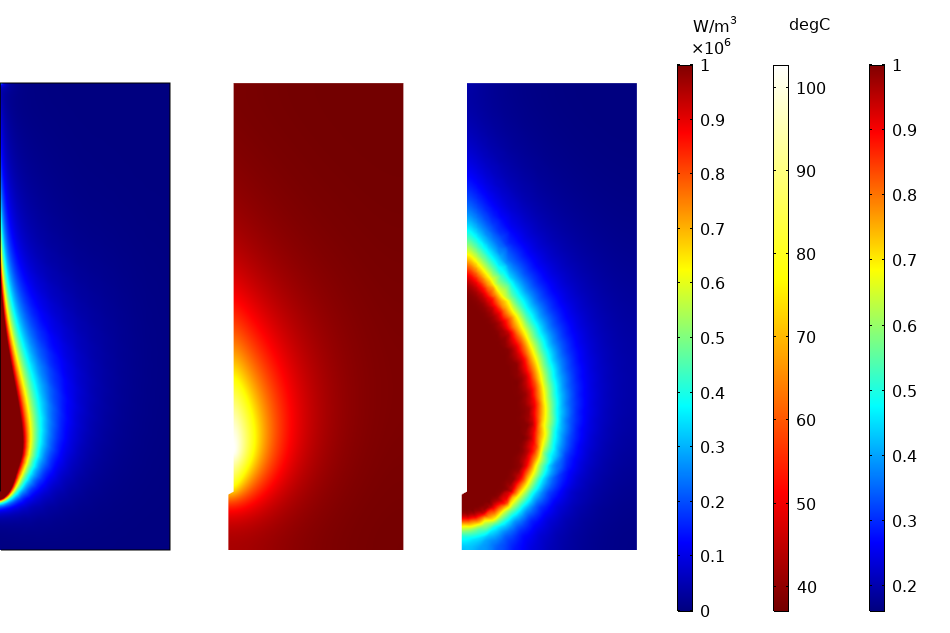
Numerical prediction of damage in tissue: surface plots for electromagnetic heat source (left), temperature (center), and damage fraction (right) after 10 minutes.
The model uses a first study step solving for the Electromagnetic Waves, Frequency Domain interface. The resistive heating term is then passed over to the transient thermal problem through the Electromagnetic Heating multiphysics coupling. A time-dependent study step involving the Bioheat Transfer interface computes the change in temperature over time and the resulting thermal damage.
The two examples presented above rely on the computing of heat transfer in biological tissue and thermal damage analysis. Let’s present in more detail the corresponding features available in COMSOL Multiphysics for the implementation of such models.
Analyzing Heat Transfer in Biological Tissue
The bioheat equation provides a standard description of heat transfer within biological tissue following Pennes’ approximation:
This equation accounts for thermal conduction and heat storage in a living tissue, modeled as a solid medium with density \rho, heat capacity C_p, and thermal conductivity k. It is predefined in the Biological Tissue feature of the Bioheat Transfer interface, with the solid tissue thermal properties available as user inputs.
Convective cooling of blood perfusion is modeled through the transfer term Q_\textrm{perf}=\rho_\textrm{b}C_{p,\textrm{b}}\omega_\textrm{b}(T_\textrm{b}-T), in which \rho_\textrm{b} is the blood density, C_{p,\textrm{b}} is the blood heat capacity, and T_\textrm{b} is the blood temperature. The blood perfusion rate, \omega_\textrm{b}, which controls the amount of cooling, may depend on space, time, temperature, or the health status of the tissue.
Blood’s thermal and flow properties are available as user inputs in the Bioheat subfeature of the Biological Tissue feature, as shown below.

The Settings window of the Bioheat feature.
Note that blood perfusion is modeled as a nondirectional heat sink, which is valid for the representation of a set of small blood vessels with isotropically distributed orientations. The cooling from larger vessels may be modeled as a boundary condition on the corresponding geometrical entities.
The electromagnetic heat source, Q_{e}, depends on the type of heating device. It is added by the Electromagnetic Heating multiphysics coupling, which also accounts for electromagnetic surface losses. Specific expressions are computed for Q_{e}, depending on which electromagnetics physics interface is included as part of the Joule Heating, Laser Heating, Induction Heating, and Microwave Heating predefined multiphysics interfaces.
Finally, heat generation from metabolism can be accounted for in the Q_\textrm{met} term. When modeling medical treatments based on tissue heating, this heat source is, in general, much smaller than the electromagnetic heat source and may be neglected.
Accounting for the Thermal Damage of Biological Tissue
Living tissue can die or be permanently damaged under specific temperature conditions. For the purpose of this blog post, let’s consider hyperthermia processes only. Cryogenic processes may be modeled by defining similar criteria involving low temperatures.
In hyperthermia processes, damage occurs either when a critical high temperature is exceeded (typically boiling), or when an excessive thermal energy is absorbed.
Correspondingly, the Thermal Damage subfeature, found under the Biological Tissue feature, includes two transformation models: Temperature threshold and Arrhenius kinetics.
The Temperature Threshold Model
The Temperature threshold model is a simple integrated inequality of how long tissue has been above a certain temperature. User-defined parameters include the Damage temperature, Damage time, and Necrosis temperature.
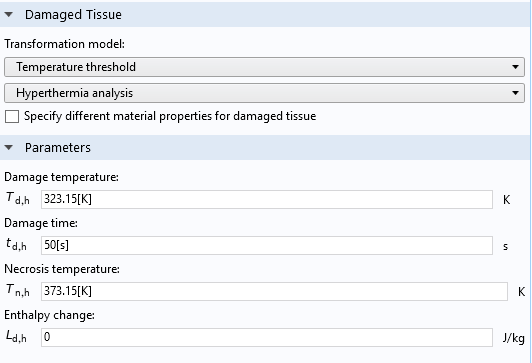
Settings window of the Thermal Damage feature, when the Temperature threshold option is selected for the Transformation model.
In this case, tissue necrosis is assumed to occur due to the following two mechanisms:
- When the tissue temperature exceeds the damage temperature T_\textrm{d,h} for more than a certain time period t_\textrm{d,h}
- Instantly after the tissue temperature exceeds the necrosis temperature T_\textrm{n,h}
The degree of tissue injury, \alpha, is expressed as:
with \alpha_0 as the initial degree of injury.
The Arrhenius Kinetics Model
The Arrhenius kinetics model uses a polynomial Arrhenius equation to directly estimate the absorbed energy. User-defined parameters include the Frequency factor and Activation energy for the integrated Arrhenius kinetics equation:
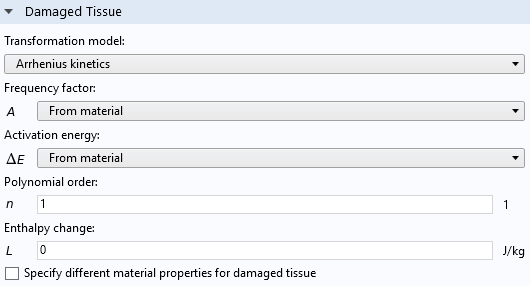
Settings window of the Thermal Damage feature, when the Arrhenius kinetics option is selected for the Transformation model.
These parameters are tissue specific and are available for generic biomaterials (Fat, Liver, Prostate, and Skin), included in the Bioheat material library in the Heat Transfer Module.
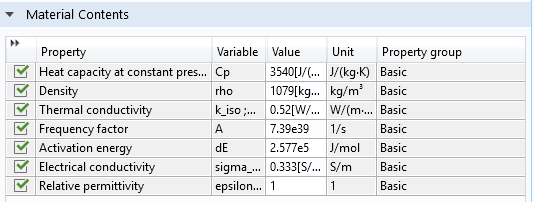
Settings window of the Liver (human) material available under the Bioheat material library.
The degree of tissue injury, \alpha, is expressed as:
Predicting the Fraction of Tissue Damage
In both models, the fraction of damage, \theta_\textrm{d}, is deduced from the degree of tissue injury, \alpha. For the temperature threshold model, \theta_\textrm{d} is either taken as the minimum between \alpha and 1, or set to 1 if the temperature exceeds or has exceeded the necrosis temperature T_\textrm{n,h}.
The plot below shows the numerical prediction of the fraction of damage at three different tissue locations for the radiofrequency example described at the beginning of this post:
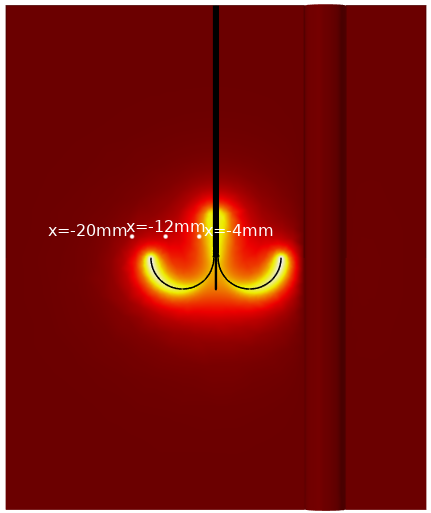
Probe positions for the evaluation of the fraction of damage, superposed on a slice of temperature distribution at time 10 minutes.
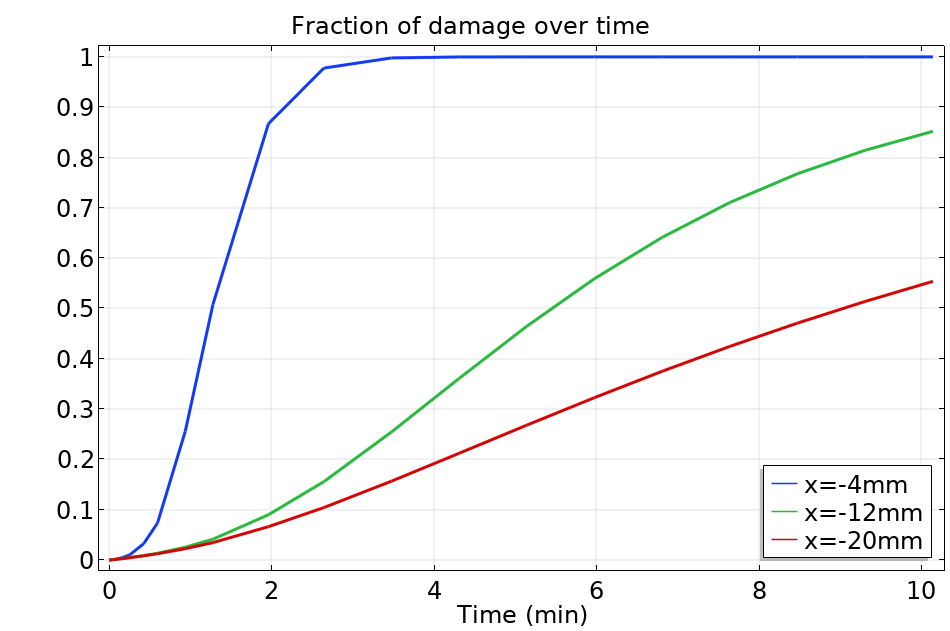
Fraction of damage at the probe positions.
Note that it is also possible to implement a user-defined equation for damage in the user interface of the Thermal Damage feature.
Specifying Material Properties for the Damaged Tissue and Handling the Damage Heat Source
Tissue damage due to hyperthermia has a feedback effect on heat transfer by altering the material properties of the biological tissue and by providing a latent heat source to the system.
By selecting the Specify different material properties for damaged tissue check box in the Thermal Damage feature, you account for the influence of tissue damage on effective heat capacity and thermal conductivity in the bioheat equation. In particular, the thermal conductivity reads:
Finally, the enthalpy variation associated to damage can be accounted for. By providing a positive value for the Enthalpy change user input in the Thermal Damage feature, you account for the heat sink associated to damage by hyperthermia.
Closing Remarks
We have described how to use the features available as part of the Heat Transfer Module for the modeling of heat transfer in biological tissue with thermal damage analysis. When considering hyperthermia cancer therapies, the physics interfaces and couplings available within the AC/DC Module complete the functionality to build a multiphysics model. The couplings between the different physical processes are summarized in the sketch below.
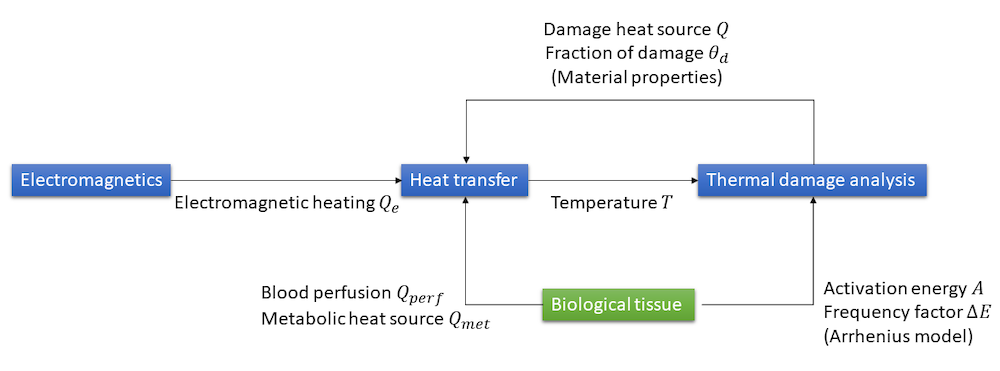
Couplings between the electromagnetics, heat transfer, and thermal damage analyses for the modeling of hyperthermia therapies.
Additional couplings, like the dependency of electrical properties upon temperature and fraction of damage, can be added to enhance the modeling.
Next Steps
Learn more about how the COMSOL® software can fit your bioheating analysis needs. Contact COMSOL to evaluate the software via the button below.
Try It Yourself
Check out the tutorial models featured in this blog post:







Comments (1)
Dany Berube
October 9, 2020Hi,
Do you know where I can find the Arrhenius coefficients for the heart (myocardium)?
Please let me know.