
Guest blogger Julia Christmann from the Alfred Wegener Institute discusses using simulation to understand the ice loss of Greenland’s glaciers…
The Greenland and Antarctic ice sheets are the world’s largest ice masses, being several-thousand kilometers in length and hundreds of meters thick. Glacier acceleration and surface melting are major contributors to sea level rise from Greenland. Viscoelastic simulations represent viscous creep and elastic short-term deformation, giving insight into the occurrence of crevasses in glaciers and iceberg calving.
Region of Interest
To reduce uncertainties in sea level rise projections, all relevant processes in ice masses have to be simulated as realistically as possible. We aimed to do that for Nioghalvfjerdsbræ (79 North Glacier, 79NG), a massive outlet glacier in northeastern Greenland. Completely gone, this glacier would raise the global sea level by ~1.1 m. It has one of the three remaining floating tongues — a floating extension in a fjord of around 70 km length — in Greenland. Ocean tides with a range of about 1 m cause the floating body to rise and fall and alter the hydrological system beneath the grounded glacier. In addition, ice experiences bending caused by ocean tides in the transition zone between grounded and freely floating ice. All those processes result in horizontal and vertical displacement variations observable by GPS measurements and satellite interferometry, and are reproducible by a finite element model in the COMSOL Multiphysics® software.

Images of the Nioghalvfjerdsbræ glacier. Images courtesy of Julia Christmann and Angelika Humbert (AWI).
Viscoelastic Simulation
Normally, large ice sheet models of Greenland only simulate the non-Newtonian viscous flow behavior of ice using a nonlinear power law for the viscosity (Glen’s flow law) that includes the effective strain rate. However, cracks and crevasses in glaciers are the nature of a solid, demonstrating that ice also behaves elastically and does so on short time scales. At the Alfred Wegener Institute (AWI) Helmholtz Centre for Polar and Marine Research, we do both large-scale ice sheet simulations and viscoelastic modeling.


Crevasses and cracks in the Nioghalvfjerdsbræ glacier. Images courtesy of Julia Christmann (AWI).
Elastic effects are also observable for tides that modify the flow of slow-moving ice on a far shorter time scale — rather than taking several years, it takes less than a day. To model both viscous and elastic effects, a Maxwell material model is appropriate, hence the deviatoric viscous stress is equal to the deviatoric elastic stress.
The stress is divided into a volume-changing (hydrostatic) part and a volume-preserving deviatoric (anisotropic) part. The stress deviator can be used to model the shape change of a material. Either the viscous or elastic strain is an unknown variable that we can include with an additional Coefficient Form PDE in COMSOL®. The momentum balance is the second equation that COMSOL® has to solve for the unknown displacements of ice motion. The derivation of this equation can be found in many books on continuum mechanics and is included as a General Form PDE in COMSOL®. For ice, the only external force that is considered in the momentum balance is gravity.
Boundary Conditions for 79NG
To adapt the general simulation of a viscoelastic Maxwell material to the conditions of 79NG, we built its irregular ice geometry and applied suitable boundary conditions. The geometry is a cross section along a central flow line of 79NG and was observed by airborne radar observations. To model a plane strain 2D cross section instead of a 3D geometry, different assumptions in the cross-flow directions have to be valid. The shape and the loading should not vary too much in the third dimension, which means the width of the considered ice domain should be sufficiently large. The stress state is independent of the third dimension, the displacement cross-flow direction is set to zero, and all strain components in the direction of the width vanish. Plane strain assumptions in the cross section of 79NG are valid, as it’s the geometry of a central flow line and the influence of lateral boundaries is negligible.
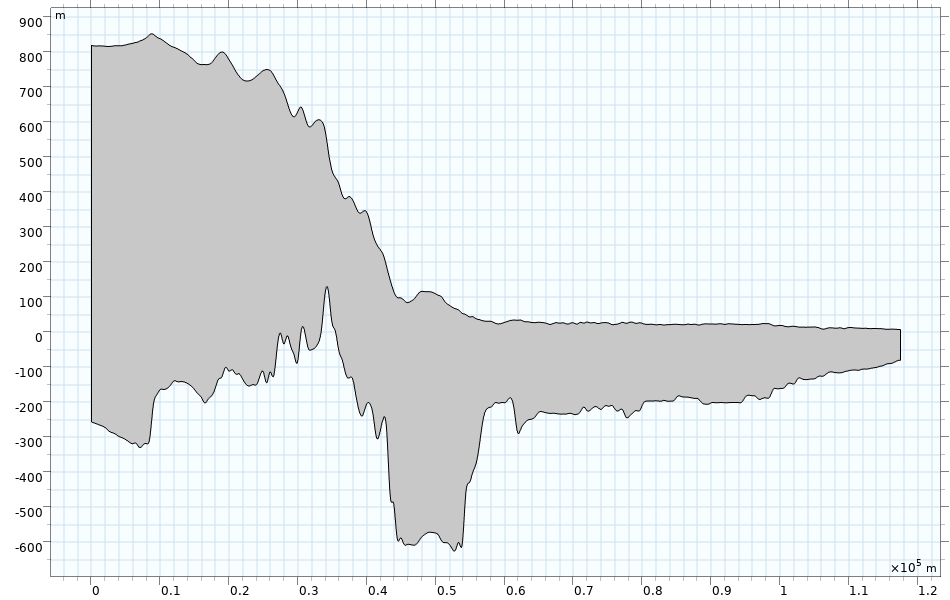
Geometry of a cross section along a central flow line of the Nioghalvfjerdsbræ glacier.
The crucial boundary conditions are the two different stress boundary conditions at the ice’s base. At the floating tongue, water pressure that can include tidal variations serves as normal stress at the base. Where the glacier is grounded, sliding is acting in the tangential plane at the base. Common sliding laws obey a nonlinear dependency of basal shear stress, the roughness of the base, effective normal pressure, and velocity. The effective normal stress is determined by the pressure in the subglacial hydrological system — the water acts as a lubricant for the ice. As it’s not sufficient to compute the subglacial water flux for a flow line only, the normal water pressure is carried over from AWI’s three-dimensional confined–unconfined aquifer system (CUAS) model. The effective pressure is the difference between ice overburden pressure and subglacial water pressure. We additionally include the tidal signal directly to the subglacial water pressure in the hydrological model: CUAS. The roughness parameter is poorly known; therefore, it’s optimized using inversion of observed surface velocities by satellite remote sensing in the Ice-Sheet and Sea-Level System Model (ISSM). ISSM is an open-source finite element flow model appropriate for continental-scale and outlet glacier applications. Using the same cross section as in the COMSOL® simulation, the ice flow is modeled by the full-Stokes equations, meaning that a viscous material law is applied.
79NG: What Insights Are Gained in the Glacier Flow of This Special Region?
Simulation results fit very well to observed tidal displacements. In the bending zone, where the ice begins to float, a phase shift is observable for the viscoelastic vertical displacement that fits the measurements. A purely viscous material simulation cannot reproduce any phase shift to the included tidal signal.
Another — even more — surprising find is that even beyond the reach of the tidal signal, elastic deformation appears. Elastic strains are found wherever the glacier flows with a speed of more than 70 cm per day (a relatively high velocity for ice) over rough bed undulations below the ice.
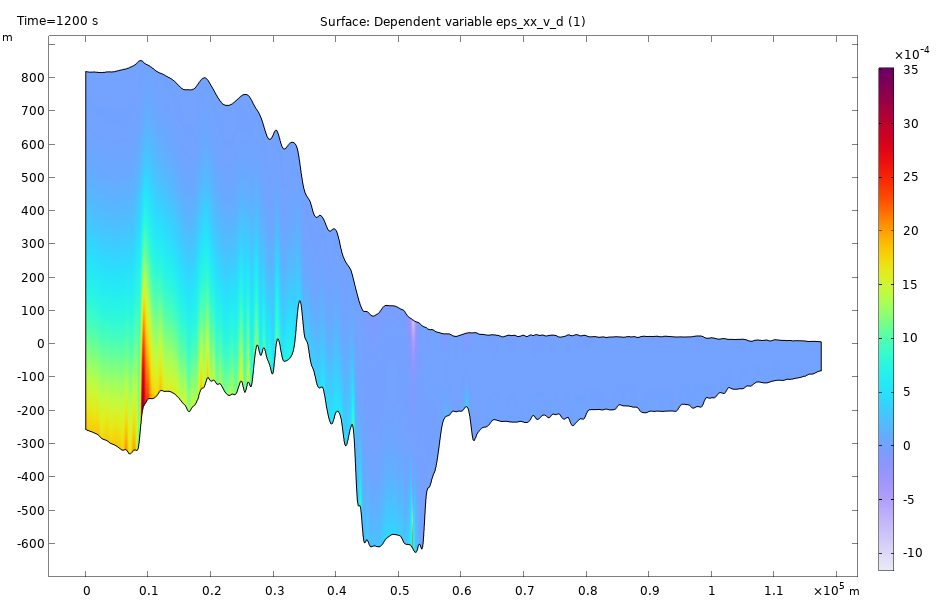
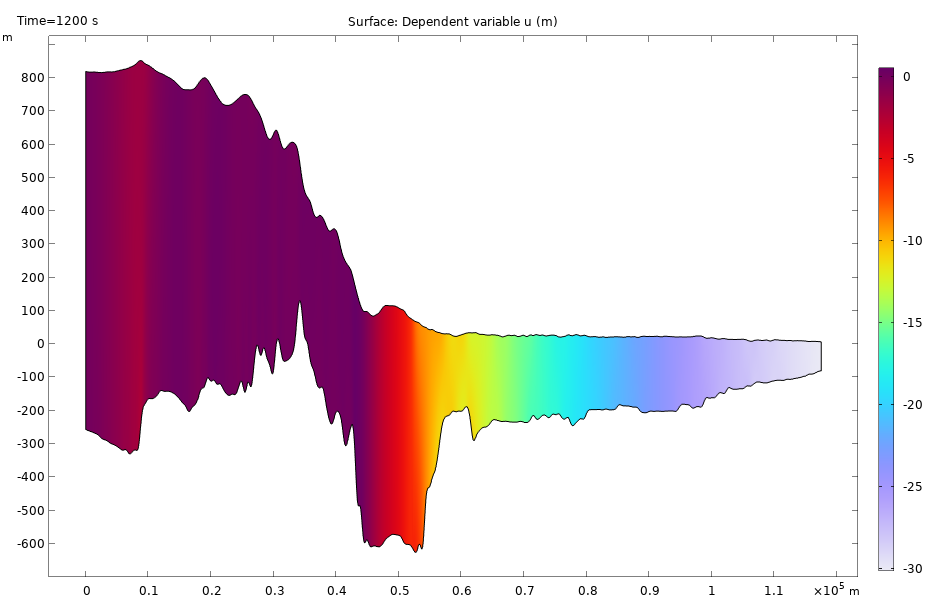
The graph on the left shows the viscous strain in flow direction shortly after the start of the simulation (t = 1200 s). The elastic strain could be computed as the difference of simulated strain (also observable by measurements) and viscous strain (internal variable in the viscoelastic model). The graph on the right shows the horizontal displacement in flow direction just after the start of the simulation (t = 1200 s) where viscous deformation is negligibly small.
Big Picture: What Does This Mean for Greenland?
At sites where we obtain high elastic strain values in our model, we can see huge fields with massive crevasses in satellite images. Those crevasse fields show that elastic deformation needs to be taken into account, as pure fluids don’t have any cracks or crevasses. However, at the moment it’s computationally not feasible or necessary to compute flow velocities in Greenland with a viscoelastic simulation. Nevertheless, one should pay special attention to regions where fast ice flows over undulated beds resulting in elastic deformation.
Acknowledgement
The outcome of our modeling study was enhanced by the availability of in situ and airborne measurements. We would like to thank the AWI field team and aircraft crew of Polar 6, who enabled the data acquisition.
About the Authors
This blog post was written by Julia Christmann, a postdoc at the Alfred Wegener Institute Helmholtz Centre for Polar and Marine Research, with help from Angelika Humbert, head of ice sheet modeling and remote sensing at the AWI Helmholtz Centre for Polar and Marine Research.
Julia Christmann graduated from the Technical University of Kaiserslautern (TUK) with a diploma thesis in applied mathematics in 2010. In 2011, she started her PhD in applied mechanics at TUK. She worked as a research scientist at TUK from 2011–2017, and in 2017 she completed her dissertation at the Institute of Applied Mechanics, TUK. She is currently a postdoctoral researcher in the Ice Modeling Group at the AWI Helmholtz Centre for Polar and Marine Research. She is also a guest lecturer on mechanics at different universities of applied science.
Angelika Humbert received her diploma thesis in physics at Technical University of Darmstadt (TU Darmstadt) in Germany in 1996. She completed her dissertation in the Department of Mechanics at TU Darmstadt in 2005. She worked as a professor of glaciology at the University of Hamburg from 2010–2012. She currently is the head of the Ice Modeling Group and Remote Sensing Group at AWI. She is also a professor for ice modeling at the University of Bremen, as well as a guest lecturer on ice mechanics at TU Darmstadt.
Related Resources
- Read the complete paper from the Alfred Wegener Institute via Nature: “Elastic deformation plays a non-negligible role in Greenland’s outlet glacier flow”
- Read our article based on their work in the User Story Gallery: “Forecasting the Ice Loss of Greenland’s Glaciers with Viscoelastic Modeling”
- Browse a related presentation on their work via Copernicus Meetings
ISSM is Copyright (c) 2008–2020, California Institute of Technology. License information available at https://issm.jpl.nasa.gov/download/.




Comments (0)