
COMSOL Multiphysics includes two interfaces for manually defining the deformation of finite element mesh, the Deformed Geometry interface and the Moving Mesh interface. In this blog post, we will address when to use these interfaces and how to use them to efficiently model translational motion.
Benefits of Using the Deformed Mesh Interfaces
Suppose we want to set up a COMSOL Multiphysics model of a solid object moving around inside of a larger domain filled with fluid such as air, or even just a vacuum. To start, let’s assume that we know what path the object will take over time. We won’t worry about which physics we need to solve the model, but we’ll assume that we want to solve for some fields in both the moving domain and the surrounding domain. Of course, we will need a finite element mesh in both of these regions, but this finite element mesh will need to change.
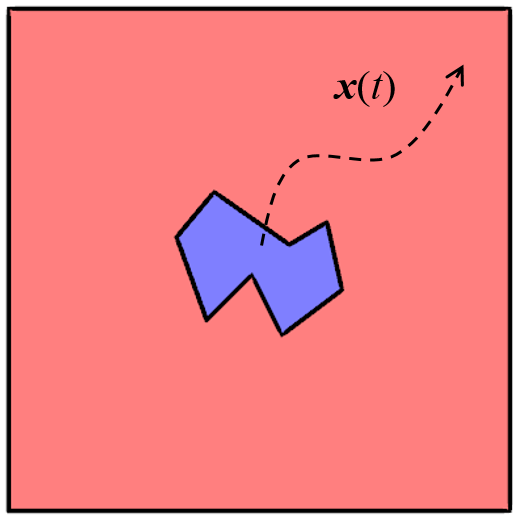
A solid object moves freely around inside of a larger domain along a known path.
For situations like this, there are two options: The Deformed Geometry interface and the Moving Mesh interface. These two interfaces actually work identically, but are meant to be used in different situations.
- The Moving Mesh interface is appropriate if we want to uniquely define the material strain at every point in the domain. It is most applicable for modeling a solid domain if the deformation of the domain can be completely defined. A change in the volume implies that the material is being stretched or compressed, but the total mass always stays the same.
- The Deformed Geometry interface is most applicable for modeling fluid, or free space, domains. If applied to a solid domain, a deformation of the boundary corresponds to a material addition or removal along that boundary. A change in the total volume of the domain implies that mass is being added or removed from the model.
The actual use of these two interfaces is identical, but choosing between them depends on which other physics you want to solve, as the interfaces handle each type of physics differently. Although we won’t cover how to choose between these two interfaces in this blog post, it is worth reading the sections “Deformed Mesh Fundamentals” and “Handling Frames in Heat Transfer” in the COMSOL Multiphysics Reference Manual as a starting point.
It is also worth mentioning that the Solid Mechanics interface cannot be combined with the Moving Mesh interface. The Solid Mechanics interface already computes the domain deformation via the balance of momentum. Other physics, such as heat transfer in solids, are solved on this deformed shape. On the other hand, it is reasonable to combine the Deformed Geometry interface with the Solid Mechanics interface if you want to study the change in stresses due to material removal, or if you want to perform a parametric sweep over a dimension without parameterizing the geometry, as described in this previous blog post.
Here, we look at the conceptual case of an object moving around inside of a larger domain with stationary boundaries, as shown in the figure above. The path of the object over time is known. We will look at how to set up the Deformed Geometry interface for this problem. But first, we need to take a quick look at which equations will be solved in COMSOL Multiphysics.
Which Equations Are Being Solved?
Our case of an object moving around inside of a domain is actually a boundary value problem. All boundaries have known displacements, and these boundary displacements can be used to define the deformation of the mesh within the interior of both domains.
There are four types of approaches for computing the deformation of the mesh within each domain: Laplace, Winslow, Hyperelastic, and Yeoh smoothing types. Here, we will address only the simplest case, referred to as a Laplace smoothing, and demonstrate how this approach is sufficient for most cases. The Laplace smoothing approach solves the following partial differential equation within the domain:
for x, and also similarly for y and z, the deformed positions of the mesh. The uppercase (X,Y,Z) are the original, underformed positions.
Since the displacements at all boundaries are known, this is a well-posed problem, and theoretically, the solution to this equation will give us the deformation of the mesh. However, in practice, we may run into cases where the computed deformation field is not very useful. This is illustrated in the figure below, which shows the original mesh on the original domain and the deformed mesh as the part is moved along the diagonal. Observe the highlighted region and note that the mesh gets highly distorted around the moving part edges, especially at sharp corners. This high distortion prevents the model from solving the above equation past a certain amount of deformation.
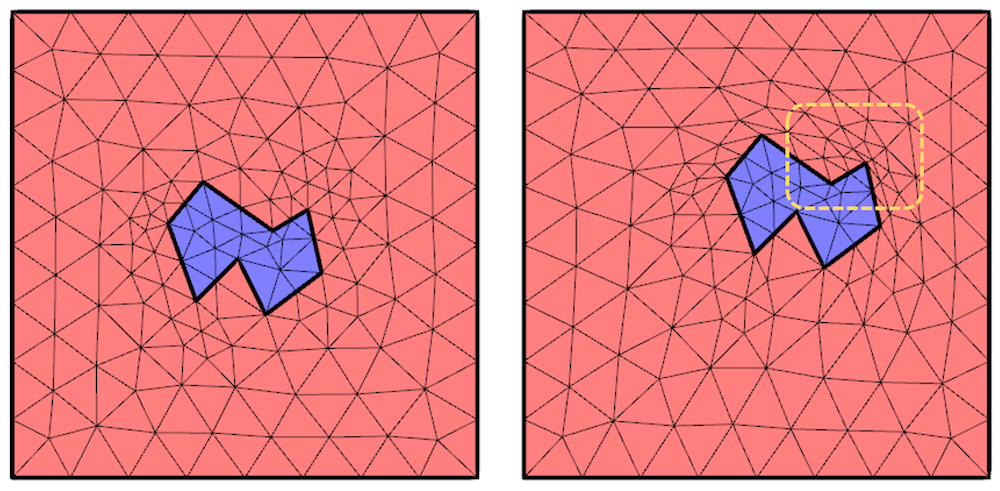
Original and deformed mesh. The region where the mesh gets highly distorted is highlighted.
In the above image, the deformation of the blue domain is completely described by its boundaries and can be prescribed. On the other hand, the deformation within the red region requires solving the above partial differential equation, and this leads to difficulties. What we want is an approach that allows us to model greater deformations while minimizing the mesh deformation.
How Can We Provide a Hint to Help the Mesh Deform?
If you have a mathematical background, you will recognize the above governing equation as Laplace’s equation and you might even know the solutions to it for a few simple cases. One of the simpler cases is the solution to Laplace’s equation on a Cartesian domain with Dirichlet boundary conditions that vary linearly along each boundary and continuously around the perimeter. For this case, the solution within the domain is equal to bilinear interpolation between the boundary conditions given at the four corners. As it turns out, you can use bilinear interpolation to find the solution to Laplace’s equation for any convex four-sided domain with straight boundaries.
The first thing that we have to do is subdivide our complicated deforming domain into convex four-sided domains with straight boundaries. One such possible subdivision is shown below.

Subdividing the domain so that the deforming region (red) is composed of four-sided convex domains.
The deforming domain is divided into convex quadrilateral domains. In fact, we could have also divided it into triangular domains since that would simply be a special case of a quadrilateral with two vertices at the same location — a so-called degenerate domain. We would only need to decompose the domain into triangles if it were not possible to split the domains into quadrilaterals.
Now that we have these additional boundaries, we need to completely define all of the boundary conditions for the deformation within the domain. The boundaries adjacent to the deforming domain are known and there is no deformation at the outside boundaries. But what about the boundaries connecting these? We have a straight line connecting two points where the deformation is known, so we could just apply linear interpolation along these lines to specify the deformation there as well.
And how can we easily compute this linear interpolation? As you might have already guessed, we can simply solve Laplace’s equation along these connecting lines!
A very general way of doing this is by adding a Coefficient Form Boundary PDE interface to our model to solve for two variables that describe the displacement along each of these four boundaries. This interface allows you to specify the coefficients of a partial differential equation to set up Laplace’s equation along a boundary. We know the displacements at the points on either end of the boundary, which gives us a fully defined and solvable boundary value problem for the displacements along the boundaries.
These new help variables completely define the deforming domains. The results are shown below and demonstrate that larger deformations of the mesh are possible. Of course, we still cannot move the object such that it collides with the boundary. That would imply that the topology of the domain would change; also, the elements cannot have zero area. We can, however, make the deformed domain very small and thin.
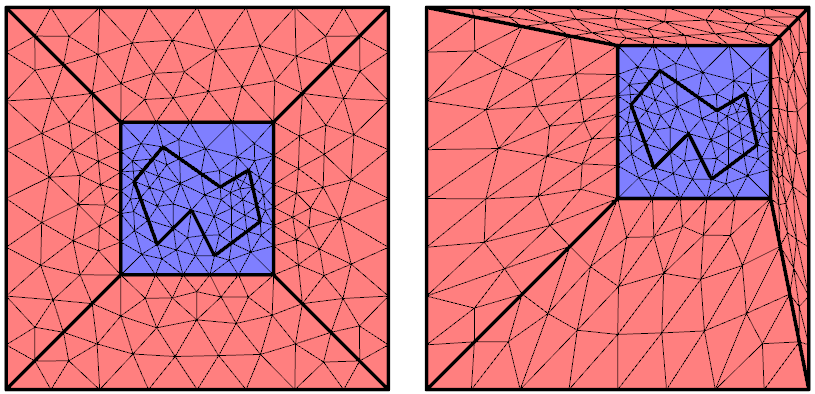
The undeformed and deformed mesh after adding the help variables for the Deformed Geometry along the interior boundaries.
You are probably thinking that the mesh shown above appears rather distorted, but keep in mind that all of these distorted elements still have straight-sided edges, which is good. In practice, you will often find that you can get good results even from what appear to be highly distorted elements.
However, we can observe that there are now very many small, distorted elements in one region and larger, stretched elements in other parts of our moving domain. The last piece of the puzzle is to use Automatic Remeshing, which will stop a transient simulation based on a mesh quality metric and remesh the current deformed shape.
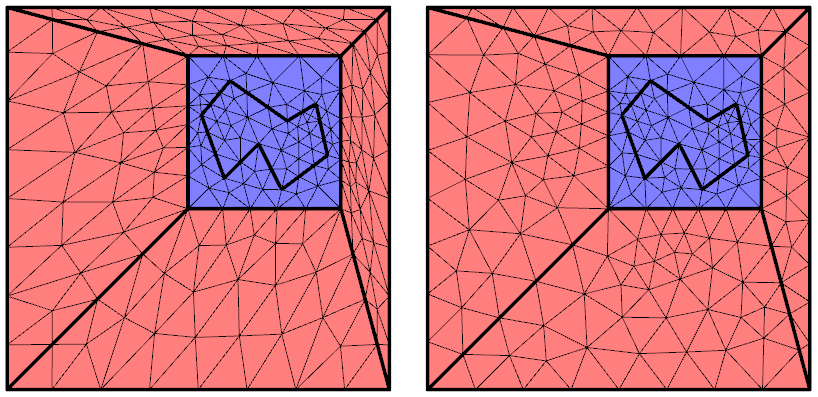
The deformed geometry immediately before and after the Automatic Remeshing step.
We can see from the above images that Automatic Remeshing leads to a lower element count in the compressed region and adds elements in the stretched region, such that the elements are reasonably uniform. This total number of elements in the mesh stays about the same. There is also an added computational burden due to the remeshing, so this step is only warranted if the element distortion adversely affects the accuracy of the results.
What if There Is Unknown Deformation?
We have looked at a case where we know exactly how our solid object will move around in our fluid domain. But what if there is an unknown deformation of the solid, such as due to some applied loads that are computed during the solution? A classic example of such a situation is a fluid-structure interaction analysis, where the deformation of the solid is due to the surrounding fluid flow.
In such situations, we can use the Integration Component Coupling operator, which makes the deformation at one point of a deforming solid structure available everywhere within the model space. The deformation of one or more points can then be used to control the deformation of the mesh. A good example of this technique is available in the Micropump Mechanism tutorial. The technique is visualized below.

When the actual deformation is unknown, an integration component coupling at a helper point can be used to control a helper line that defines the mesh deformation.
We can see in the image above that the modeling domain is actually not divided into convex quadrilaterals, and that the helper line is allowed to slide along the top boundary of the modeling domain. So this modeling approach is a little bit less strict, yet still allows the mesh to deform significantly. Hopefully it is clear that there is no single best approach to every situation. You may want to investigate a combination of techniques for your particular case.
Summary
We have described how to use the deformed mesh interfaces efficiently by decomposing the deforming domain into quadrilateral domains and introducing help variables along the boundaries. This approach makes the problem easier for the COMSOL Multiphysics software to solve. The addition of Automatic Remeshing is helpful if there is significant deformation. The approach outlined here can also be applied to 3D geometries. An example that uses both 2D and 3D cases is available here.
So far, we have only looked at translations of objects inside of relatively simple domains where it is easy to set up deforming domains. When we need to consider geometries that cannot easily be subdivided and cases with rotations of objects, we need to use a different approach. We will cover that topic in an upcoming blog post on this subject, so stay tuned!
Editor’s note: This blog post was updated on 6/25/2018 to correct an error in the section describing the Laplace smoothing approach.




Comments (9)
Brian Simonds
November 27, 2015Hi Walter, thank you for this explanation. I have no problem doing this in 2D, but getting the same concept to extent to 3D has been a problem. In both cases I have a very simple geometry. In 2D it is essentially an inner square moving along a larger square. The small inner square has a more fine mesh than the outer and “Deformed Geometry” + “Automatic Remeshing” works just fine. When I try to extend this to 3D, where you have a square moving within a larger square, I get problem where COMSOL cannot build the new meshes. Are there other techniques I could/should try? Thank you, Brian
Walter Frei
November 30, 2015 COMSOL EmployeeHello Brian, This is a question which you would want to contact COMSOL Support directly about, as it is a bit outside of the scope of this blog. Best Regards,
Parth Swaroop
July 17, 2016Dear Walter,
According to the reference manual :
To see how these smoothing methods differ, let x and y be the spatial coordinates of the spatial frame, and let X and Y be the reference coordinates of the material frame
If Laplace smoothing is selected, the software introduces deformed mesh positions x and y as degrees of freedom in the model. In the static case, it solves the equation
(∂^2 x)/(∂X^2 )+ (∂^2 x)/(∂Y^2 )
• If Winslow smoothing is selected, the software solves the equation
(∂^2 X)/(∂x^2 )+ (∂^2 X)/(∂y^2 )
Equivalently, X and Y satisfy Laplace equations as functions of the x and y coordinates.
Can you elaborate on this formulation? What is the difference between both the approach
I went through different types of frame of reference explanation before . As i understand, ALE methods uses tracking of the mesh coordinates, thus it separates it with other frame of reference.
Parth Swaroop
July 17, 2016Dear Walter,
According to the reference manual,
To see how these smoothing methods differ, let x and y be the spatial coordinates of the spatial frame, and let X and Y be the reference coordinates of the material frame
If Laplace smoothing is selected, the software introduces deformed mesh positions x and y as degrees of freedom in the model. In the static case, it solves the equation
(∂^2 x)/(∂X^2 )+ (∂^2 x)/(∂Y^2 )
• If Winslow smoothing is selected, the software solves the equation
(∂^2 X)/(∂x^2 )+ (∂^2 X)/(∂y^2 )
Equivalently, X and Y satisfy Laplace equations as functions of the x and y coordinates.
Further, i understand that, when I use deformed geometry interface, comsol introduces mesh frame of reference, which is different from material frame and geometry frame of reference. In ALE method, one would like to track this mesh coordinates of the deforming geometry. I don’t understand the above equations with respect to the above blog.
Can you elaborate more this?
Antoni Artinov
September 21, 2016Dear Walter,
thank you for this really interesting blog post and for the very good description. I am currently working on a something similar, but a bit more complex and in 3D. I studied your model these days and find out that for the zero time step t=0s we do not get the right solution, please see attachment. I solved the model just for the heat transfer without the deformed geometry and the coefficient form boundary PDE and got the right one. Actually, Comsol doesn’t solve for the zero time step, but just takes the initial values and the defined temperature on the boundaries, so I was wondering, what is the problem. Aside from that I saw that you use quadratic shape functions for the heat transfer, but as far as I know, these are not so good for heat transfer, could you say something about that.
Thanks in advance!
Best regards,
Antoni
Caty Fairclough
September 21, 2016Hi Parth and Antoni,
Thank you for your comments and for your interest in this blog post! For both of your questions, I suggest reaching out to our support team.
Online support center: https://www.comsol.com/support
Email: support@comsol.com
Best,
Caty
Antoni Artinov
June 23, 2018Dear Walter,
sorry if I am wrong, but I think the equation given in the blog post above is not correct. It should be written with respect to only one of the independent coordinate variables, e.g.:
(∂²x)/(∂X² )+ (∂²x)/(∂Y²),
and the same eq. will hold for y and z in the case of the Laplace smoothing approach. In the example btw. you solve a transient case, so I think you actually need to solve the following eq.:
(∂²(∂x/∂t))/(∂X² )+ (∂²(∂x/∂t))/(∂Y²),
In the case of the Winslow smoothing approach it will be:
(∂²X)/(∂x² )+ (∂²Y)/(∂y²),
equivalently for Y and Z.
Best regards,
Antoni Artinov
Walter Frei
June 25, 2018 COMSOL EmployeeDear Antoni,
Thank you for pointing this out, the blog has been corrected.
Best Regards,
Muhammad Roomi
June 7, 2021Hi Walter,
You have explained it very well.. Is there any tutorial which would illustrate that how would it be modeled in comsol. Thank you