
Piezoelectric valves are opened and closed by stacked piezoelectric actuators that are positioned above a seal. By applying a voltage to the stacked piezoelectric actuator, it can be made to expand or contract and the resulting deformation is used to open and close the valve. In this blog post, we feature a tutorial model of a stacked piezoelectric actuator in a pneumatic valve, new with COMSOL Multiphysics version 5.1.
Piezoelectric Valves and Stacked Actuators
Piezoelectric valves are common in medical and laboratory applications because they offer many advantages, such as energy efficiency, durability, and fast response times. To open and close the valve featured in this tutorial, there is a hyperelastic material with a piezoelectric actuator sitting on top of it. When a voltage is applied to the stacked piezoelectric actuator, it deforms in a way that either pushes the hyperelastic material against the opening of the valve to seal it or moves it away from the valve to open it.
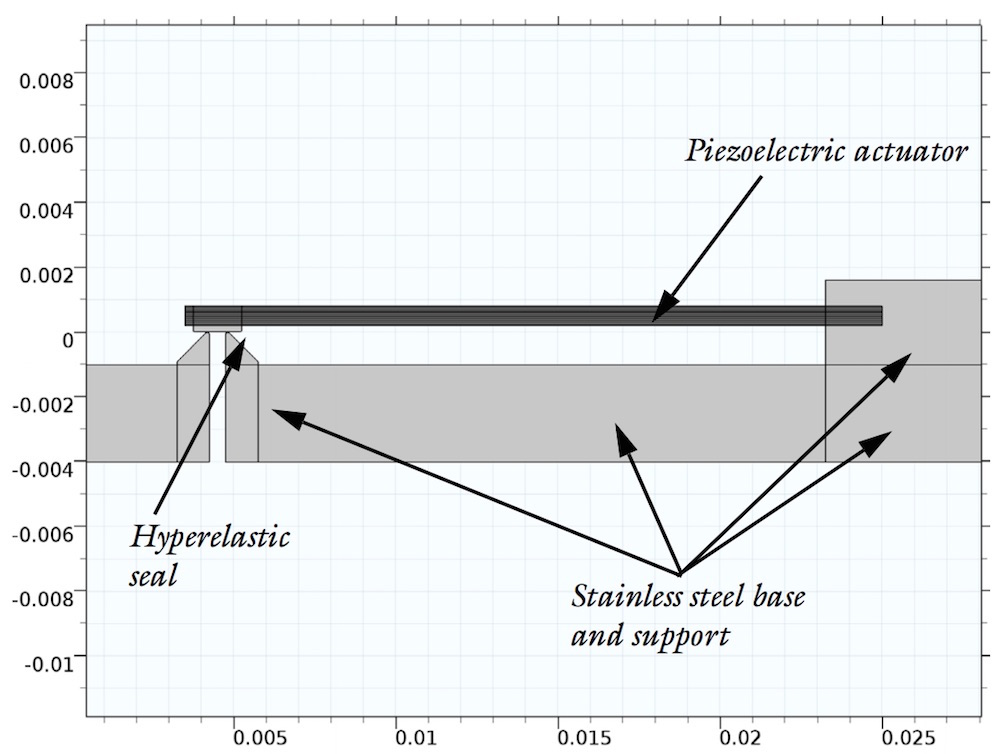
Valve, piezoelectric actuator, and seal.
Stacked piezoelectric actuators consist of two actuators stacked on top of each other. Each of the two actuators is made up of alternating layers of piezoelectric material, PZT, and very thin metal conducting layers between them. Every second metal layer is grounded, while every other layer receives an applied voltage. Similarly, the stacked PZT layers have alternating polarization directions.
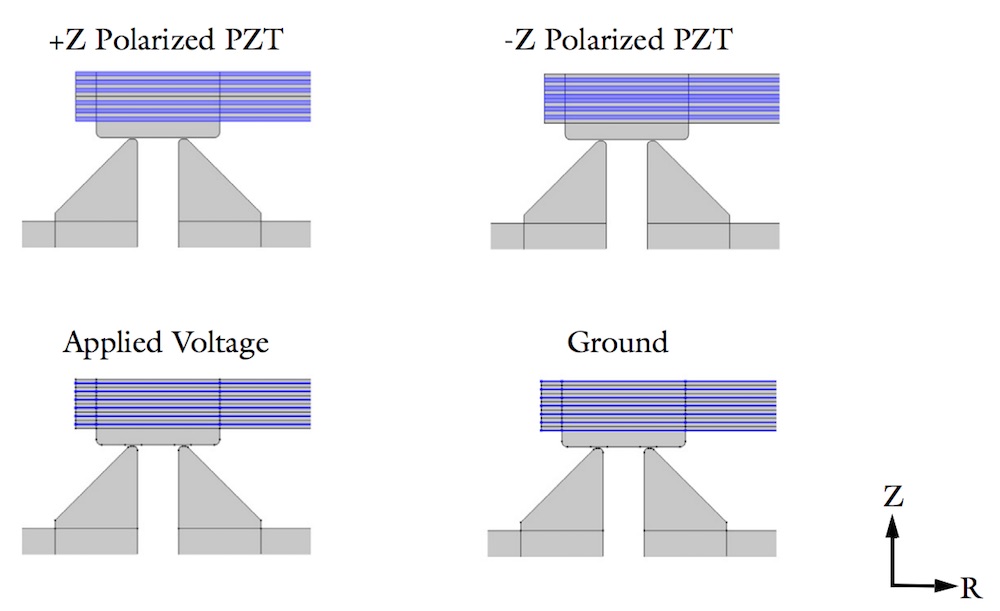
Close-ups of the actuator and seal with alternating layers of PZT and metal highlighted. The top images show the PZT layers of alternating polarization directions. The bottom images show the metal substrate with an applied voltage to every other layer and the others set to a ground.
The bimorph actuator under consideration can be thought of as two stacked actuators placed one on top of the other. For a positive applied voltage, the upper and lower actuators are designed to expand laterally and contract laterally, respectively. This results in a bending of the structure (in this case, a disc), such that the center of the disc arches downwards. This forces the hyperelastic seal into contact with the valve seat — closing the valve. In the surface plot below, the stress is indicated by the color scale.
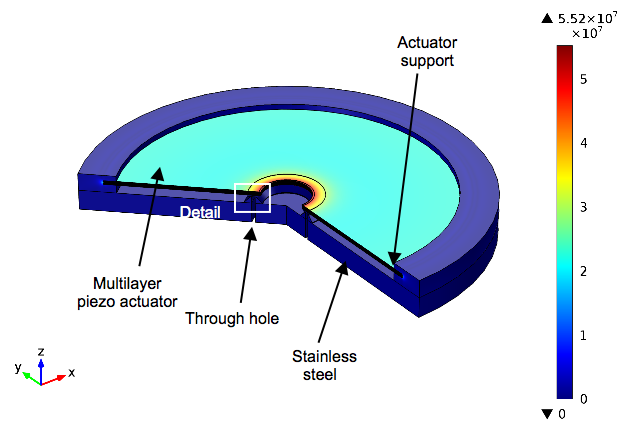
The von Mises stresses in a piezoelectric valve with a bimorph disc actuator.
Tutorial for Modeling a Stacked Piezoelectric Actuator in a Valve
The Piezoelectric Valve tutorial model, a new addition to the Application Gallery with COMSOL Multiphysics 5.1, demonstrates how to model a stacked piezoelectric bimorph disc actuator in a pneumatic valve. The MEMS Module and Nonlinear Structural Materials Module are used for this simulation.
The valve model consists of a multilayer stacked piezoelectric actuator, which in itself is a complex structure of stacked layers and electrodes. The model also includes a stainless steel substrate and a seal of hyperelastic material over the through hole of the valve.
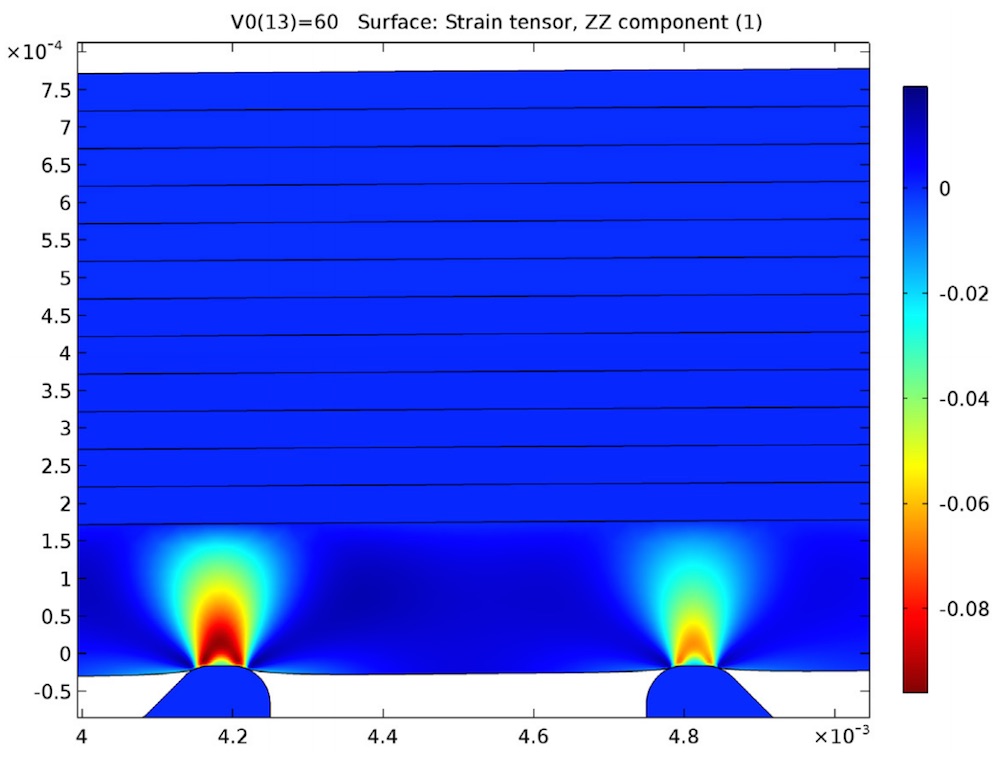
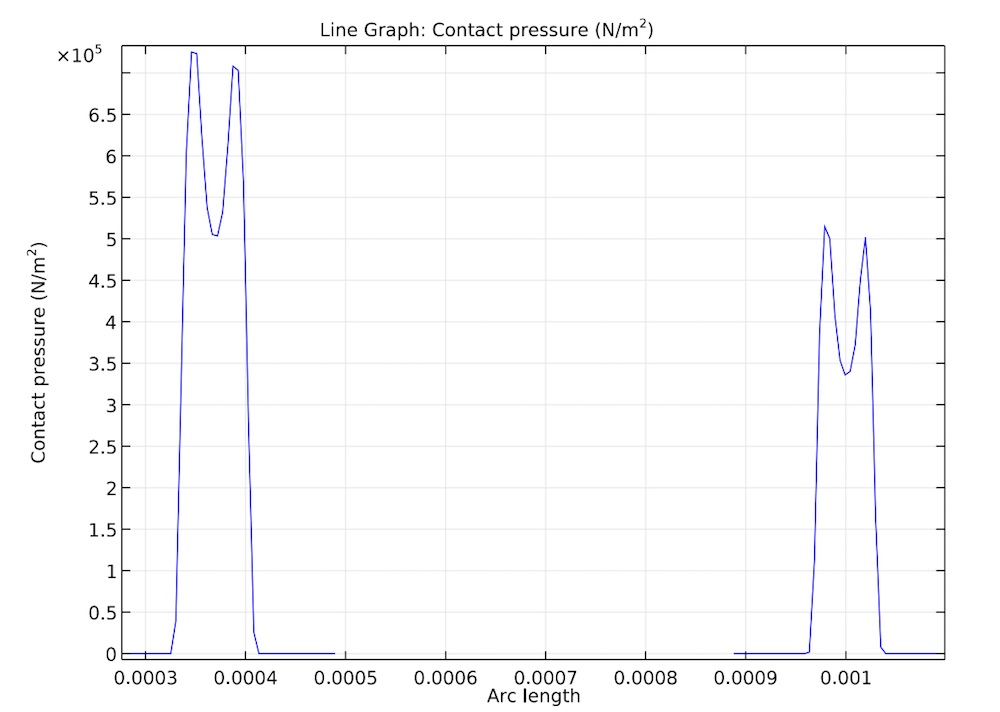
For the simulation, we apply 50 volts to the layers. The contact pressure is determined here at the two contact pressure points of the seal. We can see that deformation of the disc is greatest at the center, which compresses the hyperelastic seal against the valve’s opening and closes the valve.
Left: The strain at the two contact surfaces of the valve’s seal. Here, we can see that the deformation of the disc is greatest at the center, which closes the valve. Right: The contact pressure at the two surface points of the valve’s seal.
Modeling a piezoelectric valve allows us to analyze the operation of the stacked piezoelectric actuator and evaluate the stress and strain in the seal and the surrounding materials. The analysis could be extended to estimate the performance of the seal with different pressure differentials applied across the valve in the closed state.
Try It Yourself
- Tutorial Download: Piezoelectric Valve




Comments (0)