In chemical reaction engineering, simulations are useful for investigating and optimizing a particular reaction process or system. Modeling chemical reactions helps engineers virtually understand the chemistry, optimal size and design of the system, and how it interacts with other physics that may come into play. This is the first of a series of blog posts on chemical reaction engineering, and here we will have a look at the initial stages of modeling the application: the chemical reaction kinetics.
Why Model Chemical Reactions?
When developing chemical systems it’s of course important to gain a deep understanding of the chemical reaction process. Take the example of a monolithic reactor in a car’s exhaust system. You know that you need to reduce the noxious chemicals (in this case nitrogen oxide; NO) by a chemical (in this case ammonia; NH3) so that the gas that is emitted is less toxic. You may also know that you need enough ammonia to reduce the NO, but not so much that the ammonia goes to waste or is itself released to the atmosphere in unpleasant and even dangerous levels. Furthermore, ammonia can be depleted by oxidation — in a reaction parallel to the NO reduction.
NO reduction by ammonia:
4NO + 4NH3 + O2 → 4N2 + 6H2O
Parallel oxidation of ammonia:
4NH3 + 3O2 → 2N2 + 6H2O
The speed at which these two competing reactions occur is influenced by temperature and composition. What you don’t know — yet — is the ideal amount of ammonia to include in your system (and the size and shape of that system, more on that to come in a future blog post).
In order to figure out how much ammonia you need, to get just the right amount but not too much (the one that leaves Goldilocks smiling), you will need to study the reaction rates and the reaction kinetics associated with them. Reaction rate laws are based on hypotheses or (informed) assumptions about the chemical reaction mechanisms that in turn are supported by rigorous experiments performed under controlled circumstances. In this case “rigorous” and “controlled” are code for “time-consuming” and “difficult”. Now you tell me: would you rather do this by hand or on your computer?
Analyzing NO Reaction Kinetics in a Monolithic Reactor
Let’s suppose we are working on the NO reduction problem for a catalytic reactor, and have concluded that we need a 1:1 ratio of NH3 to NO as a lower limit based on stoichiometry. As we know from above, the ammonia is also consumed in the parallel reaction, so this ratio is bound to be higher. We’d like to analyze the reaction kinetics further and do so through selectivity, which is the ratio between the reaction rate of the NO reduction reaction and the NH3 oxidation reaction. Using COMSOL Multiphysics and the Chemical Reaction Engineering Module, we can run a series of studies to determine the optimal ratio of chemicals in our reactor.
|
|
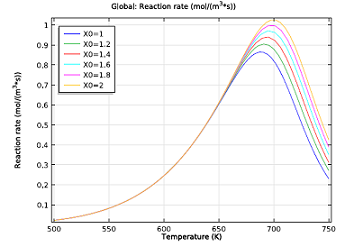
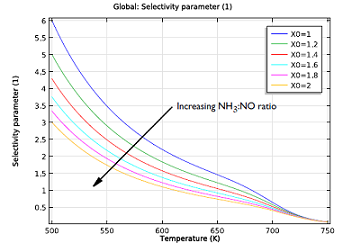
| Initial reaction rates of the NO reduction reaction, as a function of temperature. The NH3:NO ratio ranges from 1 to 2. | Selectivity parameter as a function of temperature. The reaction rate for reducing NO over oxidizing NH3 drops with both temperature and increasing the NH3:NO ratio. |
As you can see in the two figures above, the ideal working conditions would support the use of moderate temperatures, where selectivity is greater, and relatively low ratios of our two chemicals. So what’s the least amount of ammonia we need to reduce the NO in the exhaust gas?
To figure this out, we need a simple reactor model that accounts for changing reactant concentrations and temperature of the system. The figure on the left indicates that the ratio would have to be above 1.2, but could be less than 1.4. A nonisothermal plug flow reactor model will serve our purpose well here. If the exhaust gas in our example contains 41.1 mmol/m3 of NO, at a temperature of 523 K, and passes through the monolith reactor at a speed of 0.3 m/s, the model suggests an NH3:NO ratio of about 1.3 — a value that keeps the selectivity quite high. Anything less than 1.3 might lead to an ammonia shortage in our system. At 1.3, the ammonia leaving the system should also hardly be noticeable.
|
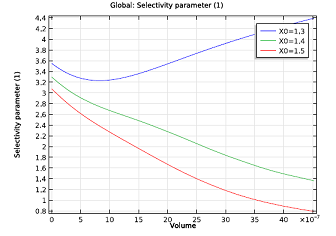
|
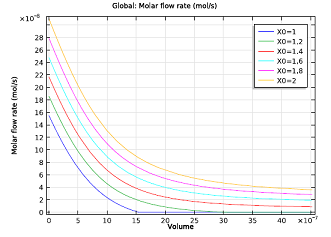
| Molar flow rate of NH3 as a function of channel volume. | Selectivity parameter as a function of channel volume. The NH3:NO ratio ranges from 1.3 to 1.5. |
Conclusion and Next Steps
As you can see here, the ideal ammonia dosage will be greatly influenced by temperature. Anyone who has designed a reactor before knows that the temperature distribution will vary from channel to channel. Therefore, our next step will be to create a full 3D model of our monolithic reactor. Stay tuned!







Comments (1)
VINAY CHANDRAKER
May 18, 2020In this problem how did you get the value of
F_O2_in 2.71e-6[mol/s] Inlet molar flow O2
F_N2_in 6.86e-5[mol/s] Inlet molar flow N2
F_H2O_in 7.34e-6[mol/s] Inlet molar flow H2O
These values are products molar flow and we know only F_NO and F_NH3 as inlet flow rates. So can you elaborate that how you found those values?