
High-intensity lasers incident upon a material that is partially transparent will deposit power into the material itself. If the absorption of the incident light can be described by the Beer-Lambert law, it is possible to model this power deposition using the core functionality of COMSOL Multiphysics. We will demonstrate how to model the absorption of the laser light and the resultant heating for a material with temperature-dependent absorptivity.
Editor’s note: For details about new functionality in this area, see our blog post “Modeling the Pulsed Laser Heating of Semitransparent Materials”.
The Beer-Lambert Law and Material Heating
When light is incident upon a semitransparent material, some of the energy will be absorbed by the material itself. If we can assume that the light is single wavelength, collimated (such as from a laser), and experiences very minimal refraction, reflection, or scattering within the material itself, then it is appropriate to model the light intensity via the Beer-Lambert law. This law can be written in differential form for the light intensity I as:
where z is the coordinate along the beam direction and \alpha(T) is the temperature-dependent absorption coefficient of the material. Because this temperature can vary in space and time, we must also solve the governing partial differential equation for temperature distribution within the material:
where the heat source term, Q, equals the absorbed light. These two equations present a bidirectionally coupled multiphysics problem that is well suited for modeling within the core architecture of COMSOL Multiphysics. Let’s find out how…
Implementation in COMSOL Multiphysics
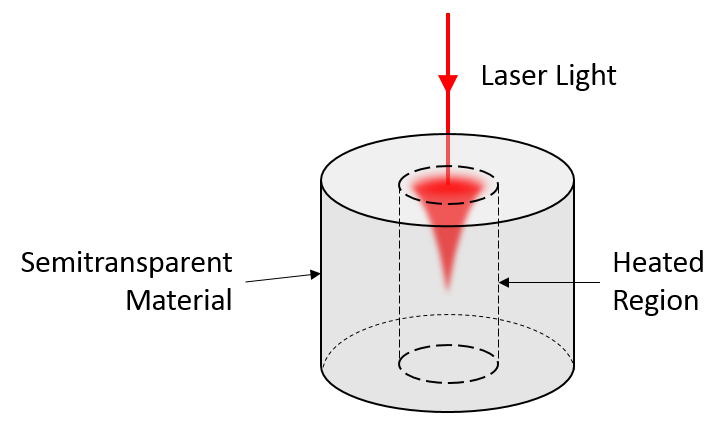
We will consider the problem shown above, which depicts a solid cylinder of material (20 mm in diameter and 25 mm in length) with a laser incident on the top. To reduce the model size, we will exploit symmetry and consider only one quarter of the entire cylinder. We will also partition the domain up into two volumes. These volumes will represent the same material, but we will only solve the Beer-Lambert law on the inside domain — the only region that the beam is heating up.
To implement the Beer-Lambert law, we will begin by adding the General Form PDE interface with the Dependent Variables and Units settings, as shown in the figure below.
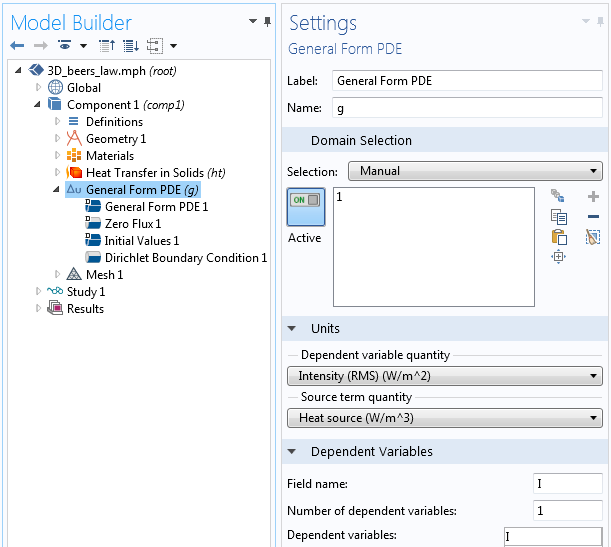
Settings for the implementing the Beer-Lambert law. Note the Units settings.
Next, the equation itself is implemented via the General Form PDE interface, as illustrated in the following screenshot. Aside from the source term, f, all terms within the equation are set to zero; thus, the equation being solved is f=0. The source term is set to Iz-(50[1/m]*(1+(T-300[K])/40[K]))*I, where the partial derivative of light intensity with respect to the z-direction is Iz, and the absorption coefficient is (50[1/m]*(1+(T-300[K])/40[K])), which introduces a temperature dependency for illustrative purposes. This one line implements the Beer-Lambert law for a material with a temperature-dependent absorption coefficient, assuming that we will also solve for the temperature field, T, in our model.
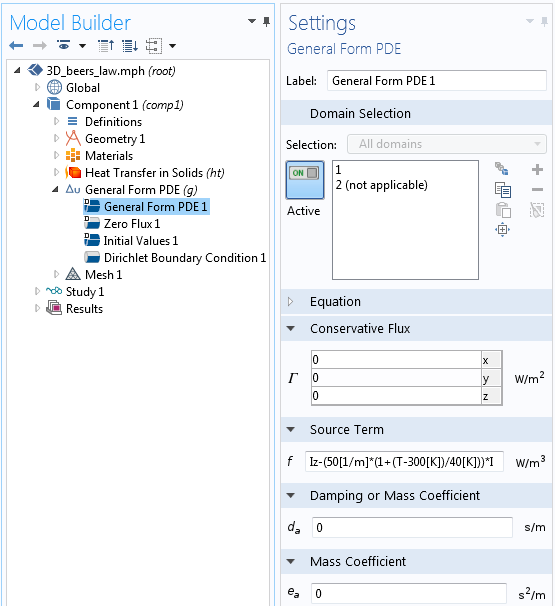
Implementation of the Beer-Lambert law with the General Form PDE interface.
Since this equation is linear and stationary, the Initial Values do not affect the solution for the intensity variable. The Zero Flux boundary condition is the natural boundary condition and does not impose a constraint or loading term. It is appropriate on most faces, with the exception of the illuminated face. We will assume that the incident laser light intensity follows a Gaussian distribution with respect to distance from the origin. At the origin, and immediately above the material, the incident intensity is 3 W/mm2. Some of the laser light will be reflected at the dielectric interface, so the intensity of light at the surface of the material is reduced to 0.95 of the incident intensity. This condition is implemented with a Dirichlet Boundary Condition. At the face opposite to the incident face, the default Zero Flux boundary condition can be physically interpreted as meaning that any light reaching that boundary will leave the domain.
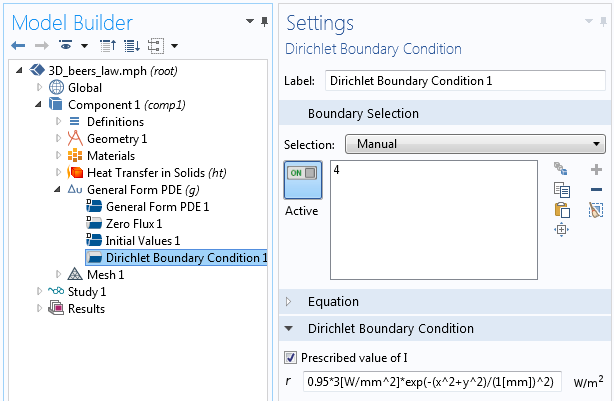
The Dirichlet Boundary Condition sets the incident light intensity within the material.
With these settings described above, the problem of temperature-dependent light absorption governed by the Beer-Lambert law has been implemented. It is, of course, also necessary to solve for the temperature variation in the material over time. We will consider an arbitrary material with a thermal conductivity of 2 W/m/K, a density of 2000 kg/m3, and a specific heat of 1000 J/kg/K that is initially at 300 K with a volumetric heat source.
The heat source itself is simply the absorption coefficient times the intensity, or equivalently, the derivative of the intensity with respect to the propagation direction, which can be entered as shown below.
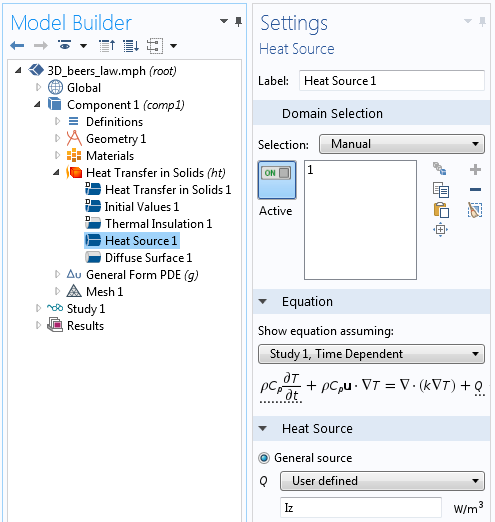
The heat source term is the absorbed light.
Most other boundaries can be left at the default Thermal Insulation, which will also be appropriate for implementing the symmetry of the temperature field. However, at the illuminated boundary, the temperature will rise significantly and radiative heat loss can occur. This can be modeled with the Diffuse Surface boundary condition, which takes the ambient temperature of the surroundings and the surface emissivity as inputs.
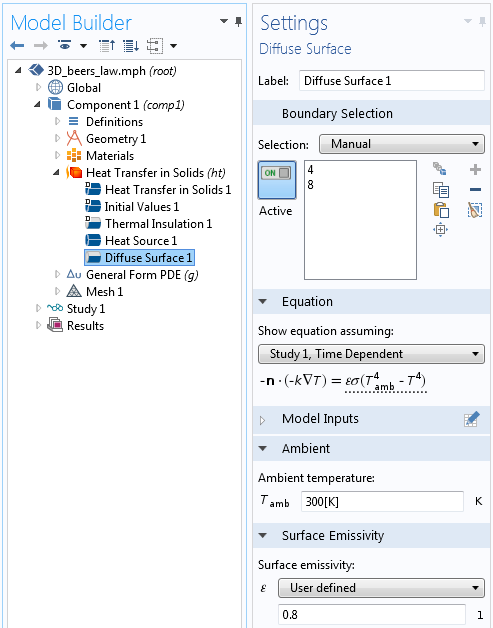
Thermal radiation from the top face to the surroundings is modeled with the Diffuse Surface boundary condition.
It is worth noting that using the Diffuse Surface boundary condition implies that the object radiates as a gray body. However, the gray body assumption would imply that this material is opaque. So how can we reconcile this with the fact that we are using the Beer-Lambert law, which is appropriate for semitransparent materials?
We can resolve this apparent discrepancy by noting that the material absorptivity is highly wavelength-dependent. At the wavelength of incident laser light that we are considering in this example, the penetration depth is large. However, when the part heats up, it will re-radiate primarily in the long-infrared regime. At long-infrared wavelengths, we can assume that the penetration depth is very small, and thus the assumption that the material bulk is opaque for emitted radiation is valid.
It is possible to solve this model either for the steady-state solution or for the transient response. The figure below shows the temperature and light intensity in the material over time, as well as the finite element mesh that is used. Although it is not necessary to use a swept mesh in the absorption direction, applying this feature provides a smooth solution for the light intensity with relatively fewer elements than a tetrahedral mesh. The plot of light intensity and temperature with respect to depth at the centerline illustrates the effect of the varying absorption coefficient due to the rise in temperature.
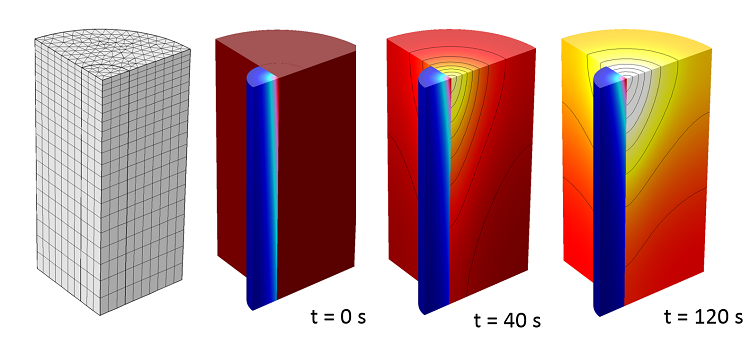
Plot of the mesh (on the far left) and the light intensity and temperature at different times.
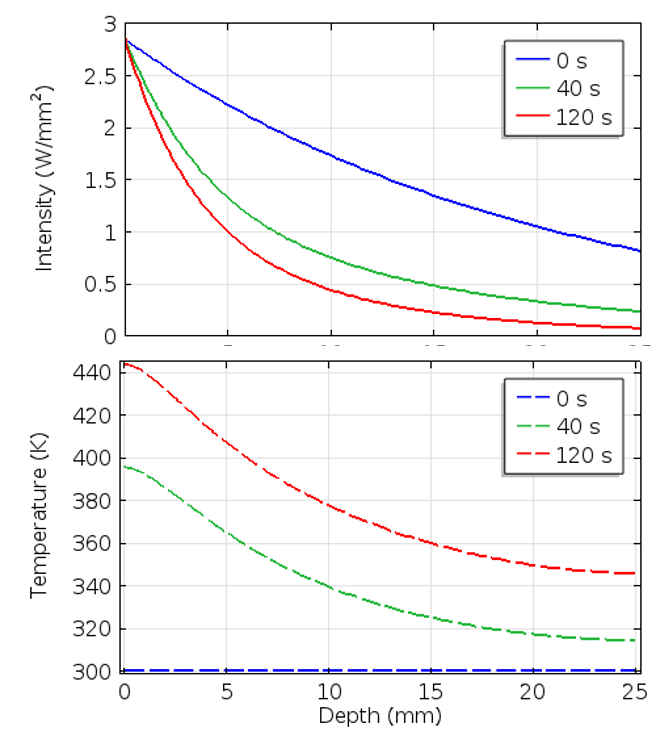
Light intensity and temperature as a function of depth along the centerline over time.
Summary and Further Refinements
Here, we have highlighted how the General Form PDE interface, available in the core COMSOL Multiphysics package, can be used for implementing the Beer-Lambert law to model the heating of a semitransparent medium with temperature-dependent absorptivity. This approach is appropriate if the incident light is collimated and at a wavelength where the material is semitransparent.
Although this approach has been presented in the context of laser heating, the incident light needs only to be collimated for this approach to be valid. The light does not need to be coherent nor single wavelength. A wide spectrum source can be broken down into a sum of several wavelength bands over which the material absorption coefficient is roughly constant, with each solved using a separate General Form PDE interface.
In the approach presented here, the material itself is assumed to be completely opaque to ambient thermal radiation. It is, however, possible to model thermal re-radiation within the material using the Radiation in Participating Media physics interface available within the Heat Transfer Module.
The Beer-Lambert law does assume that the incident laser light is perfectly collimated and propagates in a single direction. If you are instead modeling a focused laser beam with gradual variations in the intensity along the optical path then the Beam Envelopes interface in the Wave Optics Module is more appropriate.
In future blog posts, we will introduce these as well as alternate approaches for modeling laser-material interactions. Stay tuned!




Comments (56)
emma nkant
August 17, 2015Merci beaucoup.
Could I use this for 2 layers of material ? or I need special boundaries condition at the interface.
Thank you for your article.
Walter Frei
August 17, 2015 COMSOL EmployeeDear Emma,
Yes, you can use this approach for two layers of materials, simply add another “General Form PDE” interface and enter a different absorption coefficient in the different layers.
Best Regards,
Indika Perera
September 11, 2015Natan Padoin
October 5, 2015Is there a way to extend this approach to model beer-lambert law in x, y and z directions simultaneously?
Walter Frei
October 5, 2015 COMSOL EmployeeDear Natan,
If you have multiple incident beams, then you can add multiple General Form interfaces for different beam directions. If you are more generally trying to model reflection and scattering, then we suggest that you contact your COMSOL Support Team for a personalized discussion about your modeling needs.
Natan Padoin
October 5, 2015Thank you for your response. It does not work adding multiple General Form interfaces since a single domain is modeled. However, I will try another strategies.
Natan Padoin
November 11, 2015Dear Dr. Walter,
Just a remark: We got a solution to our question. Thank you!
Best regards,
Natan
nabil belghachem
January 7, 2016Dear All,
I am a beginner on COMSOL multiphysics, and concerning this tutorial I have some question , first of all I think in the Beer law is Iz=-alpha(T)* I which will give Iz+alpha(T)*I not minus; the second question is Iz is always negative so why Q=Iz and not Q=-Iz
finnally my last question why you used two different domains inside where the beam heats up and outside. I have tried it using only one domaine (the bigger cylinder) and the results were terrible
thank you for your fast reply
Best Regards,
Nabil BELGHACHEM
Walter Frei
January 7, 2016 COMSOL EmployeeDear Nabil, Yes, you are correct. One term that was assumed here that is that the beam is propagating in the negative z-direction.
Regarding your model: You would want to contact your COMSOL Support Team about this.
nabil belghachem
January 8, 2016Dear Dr Walter,
thank you very much for your fast reply. Now I understand, this make sens .
Best Regards,
Nabil BELGHACHEM
Caterina Gaudiuso
March 4, 2016Dear all,
I did not begin to use Comsol yet because I don’t know if this could be the right software to solve my problem. I would need to simulate the ultrashort laser pulses interaction with semicondutcor. To do it, I have two coupled equations for electron and lattice temperature evolution, a generalized Lambert-Beer law and an equation describing the evolution od electron density due to absorption processes. My problem is that the parameters in these equations depend on the electron and lattice temperature and on electron density (which are also dynamic variables). Do you suggest to use Comsol for this kind of problem and how?
Thank you.
Best regards.
Caterina
Walter Frei
March 4, 2016 COMSOL EmployeeDear Caterina,
What you’re describing certainly sounds like an interesting and doable problem. You may want to search on the usage of the two-temperature model in COMSOL.
If you’re looking to engage other COMSOL users, we would encourage you to post on the discussion forum:
http://www.comsol.com/community/forums/
And if you’d like to contact a COMSOL representative about purchasing a license for this type of work:
https://www.comsol.com/contact
Walter Frei
March 14, 2016 COMSOL EmployeeDear Caterina,
Briefly speaking, yes, what you are describing does all sound like a reasonable (albeit possibly quite complex) problem to solve. We would of course suggest that you investigate using COMSOL for this type of problem, yes.
Peter Woerner
May 24, 2016Walter how did you make those plots side by side. I was able to replicate your model easily enough, but not the post processing. Can you point me in the right direction?
Walter Frei
May 25, 2016 COMSOL EmployeeHello Peter, You can add a “Deformation” subfeature to any plot and specify that the plot be moved by a fixed quantity to pattern several different cases in one image. You may also find these resources helpful:
https://www.comsol.com/offers/Postprocessing-and-Visualization-Handbook-Part-1
https://www.comsol.com/offers/Postprocessing-and-Visualization-Handbook-Part-2
Bastian Geißler
September 7, 2016Hello,
thanks for the tutorial, this was very helpful. I have implemented now the Beer-Lambert-law, but now I would like to move the laser beam along a certain distance with a certain speed. How can I implement that in the existing model?
Thanks in advance,
Bastian
Walter Frei
September 7, 2016 COMSOL EmployeeHello Bastian,
Yes, you can move the location of the laser around on the surface of the part. Within the Dirichelet boundary condition simply make the expression for incident intensity a function of position and time. For an example model that shows you how to set up such time and space-dependent expressions, please see:
https://www.comsol.com/model/laser-heating-of-a-silicon-wafer-13835
Best Regards,
Bastian Geißler
October 6, 2016Hello Walter,
thanks for your help, I was able to implement the moving laser. Now I have another question:
I have two layers of material, the upper one has a low absorption coefficient, the lower one has a high absorption coefficient. The two parts have an ideal thermal contact. So basically a small amount (about 10-20%) of the laser energy is absorbed in the upper part (which has a thickness of 2 mm), the rest reaches the lower part and is absorbed in the first 100 microns of the material. Both material interactions are with beer-lambert law.
Is it possible to do this with one heat source?
At the moment I implemented simply two heat sources at the top of each layer and two dirichlet boundary conditions with the different absorptions coefficients. It would be nice to implement it in a way that if the heat reaches the lower material the beer-lambert law is calculated with the new absorption coefficient.
Thanks in advance!
Best regards,
Bastian
Walter Frei
October 10, 2016 COMSOL EmployeeHello Bastian,
What you could do, in the situation that you’re describing, is assume that the incoming light in incoherent (probably fair to do if your first layer is 2mm, and if we assume an effective wavelength of around 1um) Under those assumptions, you could implement a bi-directional Beer-Lambert law approach, solving for both forward- and backward-propagating light.
Bastian Geißler
November 3, 2016Dear all,
by the way is the equation for the gaussian intensity distribution correct? Because in literature I found the following equation: I_Gauss = I_max*exp((-2*(x^2+y^2))/r_g^2), where I_max is the maximum intensity at r = 0, and r_g is the radius of the gaussian beam. I_max is then defined as I_max = (2*P)/(pi*r_g^2), where P is the power of the laser.
Thansk in advance
Marcela Mercado Montoya
October 4, 2022Hello Bastian,
I think you are right! I replicated the model and had to adjust this parameter to have results closer to what is shown in this blog by the amazing Walter Frei. I am not getting exactly the same plots, so I suspect other parameters need to be tuned.
Great blog, thank you Walter
SEN WANG
November 17, 2016Hi Walter,
I am a beginner with comsol multiphonics. I am trying to model sunlight absorption in side a 50 micro layer of material using beer Lambert’s law. Is it appropriate to use beer Lambert’s law in my case?
My second question is about the heat source. Is it always Iz, the differential form? regardless of having the general form PDE or not? I have created a 2 D model , I don’t have the general form PDE, can the software still solve the differential form equation?
Thanks
Sen
Ciprian Plostinar
February 6, 2017Hello,
Thank you for the blog! The model appears listed in the Application Gallery but cannot be downloaded due to an html error which redirects to the current web page. Please, could you make it availbale there? Cheers!
Walter Frei
February 7, 2017 COMSOL EmployeeHello Ciprian,
This should now be addressed.
Best Regards,
Ciprian Plostinar
February 8, 2017Hello again Walter, and thank you for making the model available. It is not clear for me yet where does the 40[K] come from in the expression of the absroption coefficient. Would you clarify it for us, please? Many thanks! Ciprian
Walter Frei
March 1, 2017 COMSOL EmployeeHello Ciprian,
The 40[K] term is merely there to demonstrate a temperature dependence of the absorption coefficient. It is arbitrary, and meant just for demonstration purposes.
George Aloyan
March 20, 2017I have a question. Downloaded the model from a given link, but when I look at heat source equation, I only can choose Q=Q0, but not the one that in on the screenshot. What don’t I understand?
Thanks in advance,
George Aloyan
Caty Fairclough
March 20, 2017Hi George,
Thanks for your comment! For questions related to your modeling, please contact our support team.
Online support center: https://www.comsol.com/support
Email: support@comsol.com
Best,
Caty
George Aloyan
March 20, 2017Thank you for response.
And question about this model – why Iz is used, but not I?
Thanks in advance,
George Aloyan
Caty Fairclough
March 22, 2017Hi George,
Thank you for your additional comment. When you contact our support team, they can help address this question as well.
Best,
Caty
Saurabh Singh
May 3, 2017Hello,
This model is provided in the application gallery but the version is 5.2a. Can you please provide it in older version?
Caty Fairclough
May 15, 2017Hi Saurabh,
Thanks for your comment.
For your question, please contact our Support team.
Online Support Center: https://www.comsol.com/support
Email: support@comsol.com
Hank
August 1, 2018Hello Walter,
Thank you for the good example of laser-matter interaction with Beer-Lambert law.
I have two questions. Can a pulsed laser be applied in this example? If yes, could you please elaborate it? Also, I have the same question as Bastian has but I don’t understand what you mean by bi-directional Beer-Lambert law. Could you please also illustrate it? Thanks.
Walter Frei
August 2, 2018 COMSOL EmployeeHello Changmu,
Yes, of course, you can pulse any source. See, for example:
https://www.comsol.com/blogs/modeling-a-periodic-heat-load/
https://www.comsol.com/blogs/implementing-a-thermostat-with-the-events-interface/
Also, please note that the Heat Transfer Module (https://www.comsol.com/heat-transfer-module) now includes a “Radiative Beam in Absorbing Media” interface that will simplify this type of modeling.
Best Regards,
Sushil Kumar
September 15, 2018Hi Walter,
Thank you for the post ! I’ve some doubts please try to help me.
1. How one can used this model for multi-layer semiconductor (say 3 layer) without
considering symmetry in structure ?
2. In “General Form PDE 1” and “Dirichlet Boundary Condition” node,
“Source Term: Iz-(50[1/m ]* (1+(T-300[K])/40[K]))*I (W/m^2)” and
“Intensity Term: 0.95*3[W/mm^2]*exp(-(x^2+y^2)/(1[mm])^2)”, how and at what basis
they define like this ?
benchikh hanane
May 19, 2019Hello,
I am a biginner on comsol, i want to help me for calculate of transmitted , reflected and absorbed fraction of incident solar radiation on
benchikh hanane
May 19, 2019hello,
i am a biginner on comsol , i want to help me to caculate of transmitted , reflected and bsorbed fraction of incident solar radiation on a flat glass,
Best Regards,
Maria Ignacia Devoto Acevedo
November 8, 2019Dear Walter, would you say that this approach can be used when, instead of a monochromatic beam, I apply an electromagnetic spectrum?. I would like to calculate the temperature distribution of a stack of layers of different materials when the surface of the upper layer is exposed to solar irradiance. In my case the absorption coefficient for each material/layer will only depend on the wavelength but constant under temperature changes.
There are maybe other physics interfaces that are easier to use when the problem is wavelength dependent? I was also thinking in “Radiative Beam in Absorbing Media” but I do not know if this addresses the spectrum of radiation.
Best wishes.
Ignacia.
Massimiliano Benetti
February 28, 2020Dear Walter,
if I understand correctly to model two layers, I have to add another “General Form PDE” interface and enter a different absorption coefficient in the different layers. I guess I have to consider another Dirichlet Boudariy Codition at the bounday between the two layers. I’m not sure which value is more appropriate to assign to this Dirichlet Boudariy Codition: I? How can I model the reflection of this boundary?
Thanks
Meijun Chen
April 21, 2020Hi everyone,
Just a simple question: where is I defined? I do not see it in Parameters or anywhere, and I am confused about how the whole thing work without knowing how much I is. Is it in Dirichlet Boundary Condition?
Thanks if anyone gives me a hint!
Yours,
Meijun
Yateendra Sihag
October 2, 2020Yes it is defined in the Dirichlet Boundary Condition.
Walter Frei
April 21, 2020 COMSOL EmployeeHello,
Please note that the Heat Transfer Module (https://www.comsol.com/heat-transfer-module) now includes a “Radiative Beam in Absorbing Media” interface that will simplify this type of modeling. There is no longer a reason to follow this example.
Yateendra Sihag
October 2, 2020Dear Walter,
Could you please tell me what is the spot size of gaussian laser beam you have considered here, I am unable to find it in the given gaussian equation.
Walter Frei
October 2, 2020 COMSOL EmployeeHello Yateendra,
The Dirichlet Boundary Condition sets the incident light intensity, and contains an expression in terms of x and y that defines the profile of the beam intensity.
ramesh sanga
December 7, 2020hello walter,
Can i use this approach for spectroscopy application of beer lambert’s law.
Farzaneh Ab.
October 30, 2020Dear Walter,
Thanks for the nice blog post!
In the blog, there is a paragraph discussing on why we still account for the surface-to-ambient radiation even if the medium is transparent, and it say “when the part heats up, it will re-radiate primarily in the long-infrared regime. At long-infrared wavelengths, we can assume that the penetration depth is very small, and thus the assumption that the material bulk is opaque for emitted radiation is valid.”
The material that I’m interested to model is ZnSe glass which is still transparent at the long-wave infrared regime ranges from 8 μm to 12 μm. The laser wavelength in my example is operating at 10.6 um (CO2). Do you have any suggestion to how to modify Surface-to-ambient radiation for this kind of material?
Mohamad Barekati Goudarzi
November 30, 2020Dear Walter, Is there any video recording of the problem modeling that we can use as tutorial?
Julian Anaya
January 26, 2021I know that this is an old post, but for other reasons I found this work published elsewhere…
https://www.intechopen.com/books/modern-spectroscopic-techniques-and-applications/analysis-of-the-absorption-phenomenon-through-the-use-of-finite-element-method
Quite interestingly they have just copied all your words, even the material properties given in your toy model are used for “alpha brass…” I think it is plagiarism at its worst.
Anyway, I’ve noted that the solution stated here for the PDE is OK for this case, but when the coefficient of absorption varies in depth the solution becomes worse. If the coefficient of absorption is defined as 0 if Z>10mm, Alpha if Z<10 mm, then the solution makes no real sense, right? Just a warning in case someones copies this in another paper/chapter without checking that range of validity…
Walter Frei
January 26, 2021 COMSOL EmployeeHi Julian,
Thank you for the comment. Perhaps (at least for us) it is best to say that “imitation is the sincerest form of flattery” and leave it to the peer review process to sort out.
You’re correct in that one needs to be very careful in understanding the regime of validity of this equation. This equation is the unidirectional Beer-Lambert law and assumes a “slowly-varying” absorption and no (or minimal) change in permittivity and/or permeability. If there is a step change in these properties, then one would need to apply the Fresnel Equations (by hand) to compute the intensity of reflected/refracted energy at the interface.
With the new (actually not-so-new) “Radiative Beam in Absorbing Media” interface within the Heat Transfer Module, it is easily possible to account for an arbitrary number of different beam directions, which would make this simpler to do. A follow-up article on that is likely warranted.
For the case you describe, there is actually an even better simplification. If the absorption coefficient is zero, then don’t solve for this equation at all, since the intensity profile will not change. Insert a boundary into the modeling domain that describes where the loss starts to be non-zero. That is at least one approach that springs to mind.
Julian Anaya
January 26, 2021Thanks Walter.
The thing is that the absorption goes is T dep and there is a region of absorption in the middle, so I cannot really use those tricks…
Kind regards,
Julian
Walter Frei
January 26, 2021 COMSOL EmployeeHi Julian, Yes, we should also cover the cases where the Beer-Lambert law does not hold. In that case, one would need to look to the Ray Optics (most likely start here) or Beam Envelope, or even the Full-Wave Electromagnetic approach (the full-wave is the most expensive). An overview of these is given here:
https://www.comsol.com/blogs/modeling-laser-material-interactions-in-comsol-multiphysics/
sijin wang
April 10, 2021Hi, in the equation (50[1/m]*(1+(T-300[K])/40[K])) is the T here refers to the temperature at the local mesh or the average temperature of the whole object? Or in other words, is absorption coefficient defined uniformly for the material or it is non-uniform depending on the local temperature?
sijin wang
April 11, 2021Hi, I am new to COMSOL Multiphysics. I used this model to simulate a single pulse laser beam on a silicon wafer with 0.1mJ pulse length 100ns and 1065ns wavelength. In reality one pulse is large enough to melt the silicon but in COMSOL the temperature is not high enough. I did compensate the temperature change for absorption coefficient. I am wandering can this model handle the very short pulse like 100ns?
Runnan Lou
October 7, 2024Dear Frei,
Thanks for your example. But I think you should firstly work on the model from “Temperature rise induced by a laser beam” by M.Lax, in order to convince people your model setup is correct. Since I got completely different results based on your setup and the value mention in that paper.
Walter Frei
October 7, 2024 COMSOL EmployeeHello Runnan,
That certainly is an interesting observation, and bears a philosophical response: How would you work to convince people that the setup of a model that you have built is correct? What are all the possible conclusions that a reader could arrive at when you make the statement that your are not getting the expected results, and how would you address those?
Runnan Lou
October 7, 2024Sorry, no offense. Firstly, this paper in question has been cited 810 times, and I have tested its results with several other models, all of which show consistent outcomes. Currently, I am attempting to replicate the results using COMSOL, but I have encountered discrepancies. I believe this may be due to the assumption of a semi-infinite geometry, where allows heat diffuses without limitation. I think I have figured out the correct boundary conditions. Again thanks for your example. My point is it is better to build up a model with well-known references so people can easily follow.