Modeling of Materials in Wave Electromagnetics Problems

Whenever we are solving a wave electromagnetics problem in COMSOL Multiphysics, we build a model that is composed of domains and boundary conditions. Within the domains, we use various material models to represent a wide range of substances. However, from a mathematical point of view, all of these different materials end up being handled identically within the governing equation. Let’s take a look at these various material models and discuss when to use them.

What Equations Are We Solving?

Here, we will speak about the frequency-domain form of Maxwell’s equations in the Electromagnetic Waves, Frequency Domain interface available in the RF Module and the Wave Optics Module. The information presented here also applies to the Electromagnetic Waves, Beam Envelopes formulation in the Wave Optics Module.

Under the assumption that material response is linear with field strength, we formulate Maxwell’s equations in the frequency domain, so the governing equations can be written as:

This equation solves for the electric field, \mathbf{E}, at the operating (angular) frequency \omega = 2 \pi f (c_0 is the speed of light in vacuum). The other inputs are the material properties \mu_r, the relative permeability; \epsilon_r, the relative permittivity; and \sigma , the electrical conductivity. All of these material inputs can be positive or negative, real or complex-valued numbers, and they can be scalar or tensor quantities. These material properties can vary as a function of frequency as well, though it is not always necessary to consider this variation if we are only looking at a relatively narrow frequency range.

Let us now explore each of these material properties in detail.

Electrical Conductivity

The electrical conductivity quantifies how well a material conducts current — it is the inverse of the electrical resistivity. The material conductivity is measured under steady-state (DC) conditions, and we can see from the above equation that as the frequency increases, the effective resistivity of the material increases. We typically assume that the conductivity is constant with frequency, and later on we will examine different models for handling materials with frequency-dependent conductivity.

Any material with non-zero conductivity will conduct current in an applied electric field and dissipate energy as a resistive loss, also called Joule heating. This will often lead to a measurable rise in temperature, which will alter the conductivity. You can enter any function or tabular data for variation of conductivity with temperature, and there is also a built-in model for linearized resistivity.

Linearized Resistivity is a commonly used model for the variation of conductivity with temperature, given by:

where \rho_0 is the reference resistivity, T_{ref} is the reference temperature, and \alpha is the resistivity temperature coefficient. The spatially-varying temperature field, T, can either be specified or computed.

Conductivity is entered as a real-valued number, but it can be anisotropic, meaning that the material’s conductivity varies in different coordinate directions. This is an appropriate approach if you have, for example, a laminated material in which you do not want to explicitly model the individual layers. You can enter a homogenized conductivity for the composite material, which would be either experimentally determined or computed from a separate analysis.

Within the RF Module, there are two other options for computing a homogenized conductivity: Archie’s Law for computing effective conductivity of non-conductive porous media filled with conductive liquid and a Porous Media model for mixtures of materials.

Archie’s Law is a model typically used for the modeling of soils saturated with seawater or crude oil, fluids with relatively higher conductivity compared to the soil.

Porous Media refers to a model that has three different options for computing an effective conductivity for a mixture of up to five materials. First, the Volume Average, Conductivity formulation is:

where \theta is the volume fraction of each material. This model is appropriate if the material conductivities are similar. If the conductivities are quite different, the Volume Average, Resistivity formulation is more appropriate:

Lastly, the Power Law formulation will give a conductivity lying between the other two formulations:

These models are all only appropriate to use if the length scale over which the material properties’ change is much smaller than the wavelength.

Relative Permittivity

The relative permittivity quantifies how well a material is polarized in response to an applied electric field. It is typical to call any material with \epsilon_r>1 a dielectric material, though even vacuum (\epsilon_r=1) can be called a dielectric. It is also common to use the term dielectric constant to refer to a material’s relative permittivity.

A material’s relative permittivity is often given as a complex-valued number, where the negative imaginary component represents the loss in the material as the electric field changes direction over time. Any material experiencing a time-varying electric field will dissipate some of the electrical energy as heat. Known as dielectric loss, this results from the change in shape of the electron clouds around the atoms as the electric fields change. Dielectric loss is conceptually distinct from the resistive loss discussed earlier; however, from a mathematical point of view, they are actually handled identically — as a complex-valued term in the governing equation. Keep in mind that COMSOL Multiphysics follows the convention that a negative imaginary component (a positive-valued electrical conductivity) will lead to loss, while a positive complex component (a negative-valued electrical conductivity) will lead to gain within the material.

There are seven different material models for the relative permittivity. Let’s take a look at each of these models.

Relative Permittivity is the default option for the RF Module. A real- or complex-valued scalar or tensor value can be entered. The same Porous Media models described above for the electrical conductivity can be used for the relative permittivity.

Refractive Index is the default option for the Wave Optics Module. You separately enter the real and imaginary part of the refractive index, called n and k, and the relative permittivity is \epsilon_r=(n-jk)^2. This material model assumes zero conductivity and unit relative permeability.

Loss Tangent involves entering a real-valued relative permittivity, \epsilon_r&#39, and a scalar loss tangent, \delta. The relative permittivity is computed via \epsilon_r=\epsilon_r&#39(1-j \tan \delta), and the material conductivity is zero.

Dielectric Loss is the option for entering the real and imaginary components of the relative permittivity \epsilon_r=\epsilon_r&#39-j \epsilon_r&#39&#39. Be careful to note the sign: Entering a positive-valued real number for the imaginary component \epsilon_r&#39&#39 when using this interface will lead to loss, since the multiplication by -j is done within the software. For an example of the appropriate usage of this material model, please see the Optical Scattering off of a Gold Nanosphere tutorial.

The Drude-Lorentz Dispersion model is a material model that was developed based upon the Drude free electron model and the Lorentz oscillator model. The Drude model (when \omega_0=0) is used for metals and doped semiconductors, while the Lorentz model describes resonant phenomena such as phonon modes and interband transitions. With the sum term, the combination of these two models can accurately describe a wide array of solid materials. It predicts the frequency-dependent variation of complex relative permittivity as:

where \epsilon_{\infty} is the high-frequency contribution to the relative permittivity, \omega_p is the plasma frequency, f_k is the oscillator strength, \omega_{0k} is the resonance frequency, and \Gamma_k is the damping coefficient. Since this model computes a complex-valued permittivity, the conductivity inside of COMSOL Multiphysics is set to zero. This approach is one way of modeling frequency-dependent conductivity.

The Debye Dispersion model is a material model that was developed by Peter Debye and is based on polarization relaxation times. The model is primarily used for polar liquids. It predicts the frequency-dependent variation of complex relative permittivity as:

where \epsilon_{\infty} is the high-frequency contribution to the relative permittivity, \Delta \epsilon_k is the contribution to the relative permittivity, and \tau_k is the relaxation time. Since this model computes a complex-valued permittivity, the conductivity is assumed to be zero. This is an alternate way to model frequency-dependent conductivity.

The Sellmeier Dispersion model is available in the Wave Optics Module and is typically used for optical materials. It assumes zero conductivity and unit relative permeability and defines the relative permittivity in terms of the operating wavelength, \lambda, rather than frequency:

where the coefficients B_k and C_k determine the relative permittivity.

The choice between these seven models will be dictated by the way the material properties are available to you in the technical literature. Keep in mind that, mathematically speaking, they enter the governing equation identically.

Relative Permeability

The relative permeability quantifies how a material responds to a magnetic field. Any material with \mu_r>1 is typically referred to as a magnetic material. The most common magnetic material on Earth is iron, but pure iron is rarely used for RF or optical applications. It is more typical to work with materials that are ferrimagnetic. Such materials exhibit strong magnetic properties with an anisotropy that can be controlled by an applied DC magnetic field. Opposed to iron, ferrimagnetic materials have a very low conductivity, so that high-frequency electromagnetic fields are able to penetrate into and interact with the bulk material. This tutorial demonstrates how to model ferrimagnetic materials.

There are two options available for specifying relative permeability: The Relative Permeability model, which is the default for the RF Module, and the Magnetic Losses model. The Relative Permeability model allows you to enter a real- or complex-valued scalar or tensor value. The same Porous Media models described above for the electrical conductivity can be used for the relative permeability. The Magnetic Losses model is analogous to the Dielectric Loss model described above in that you enter the real and imaginary components of the relative permeability as real-valued numbers. An imaginary-valued permeability will lead to a magnetic loss in the material.

Modeling and Meshing Notes

In any electromagnetic modeling, one of the most important things to keep in mind is the concept of skin depth, the distance into a material over which the fields fall off to 1/e of their value at the surface. Skin depth is defined as:

where we have seen that relative permittivity and permeability can be complex-valued.

You should always check the skin depth and compare it to the characteristic size of the domains in your model. If the skin depth is much smaller than the object, you should instead model the domain as a boundary condition as described here: “Modeling Metallic Objects in Wave Electromagnetics Problems“. If the skin depth is comparable to or larger than the object size, then the electromagnetic fields will penetrate into the object and interact significantly within the domain.

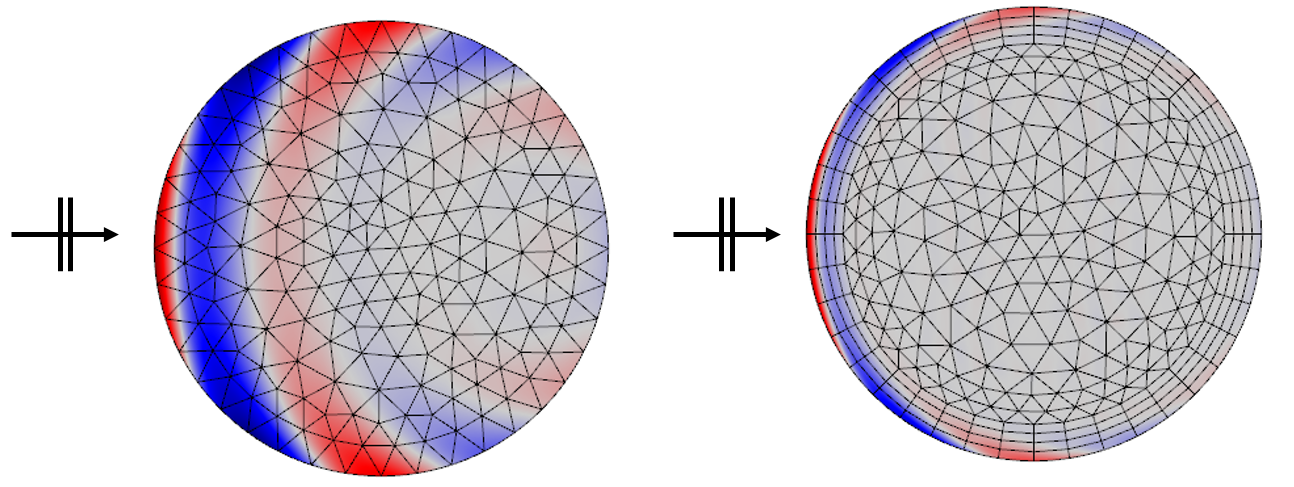
A plane wave incident upon objects of different conductivities and hence different skin depths. When the skin depth is smaller than the wavelength, a boundary layer mesh is used (right). The electric field is plotted.

If the skin depth is smaller than the object, it is advised to use boundary layer meshing to resolve the strong variations in the fields in the direction normal to the boundary, with a minimum of one element per skin depth and a minimum of three boundary layer elements. If the skin depth is larger than the effective wavelength in the medium, it is sufficient to resolve the wavelength in the medium itself with five elements per wavelength, as shown in the left figure above.

Summary

In this blog post, we have looked at the various options available for defining the material properties within your electromagnetic wave models in COMSOL Multiphysics. We have seen that the material models for defining the relative permittivity are appropriate even for metals over a certain frequency range. On the other hand, we can also define metal domains via boundary conditions, as previously highlighted on the blog. Along with earlier blog posts on modeling open boundary conditions and modeling ports, we have now covered almost all of the fundamentals of modeling electromagnetic waves. There are, however, a few more points that remain. Stay tuned!