
Grind grain into flour, then add water and pressure to make dough, and then cut it up and boil it; pasta seems like pretty basic stuff. And yet, something about it seems to inspire creativity, and not just in the kitchen. We like telling tales about it, too. Did you ever hear that Marco Polo discovered pasta in 13th-century China and then introduced it to Italy? It’s not true, as wheat-based pasta was already being eaten in ancient Rome and Greece (Ref. 1).
Here’s another dubious tale, this one a lesson from my childhood on not believing everything we hear: According to one of my grade school teachers, “Italian mamas” would test pasta’s doneness by pulling some from the pot and throwing it at the wall to see if it stuck. Really? In all nine years of my life, I had never seen my Italian–American grandmother toss even a single noodle!
What makes such slippery narratives so in-grained? Could it simply be that pasta, like people, is more complex than it may seem on the surface? Read on as we untangle the facts about making pasta, with help from a tutorial model of a commercial pasta extruding machine.
The Balancing Act of Pasta Rheology
Art and science, flour and water, aglio e olio; whether we’re manufacturing noodles or making them into dinner, we must balance tensions among complementary elements. The grains from which pasta flour is made contain both starches and proteins. To make dough, we add water to the flour and then agitate it with our hands or tools. The added moisture and stresses of this process will turn a wet powder into a sticky, stretchy blob.


At left: Women making pasta in an Italian illustration from the 15th century. Image in the public domain via Wikimedia Commons. At right: A man hand-pulling noodles in Dalian, Liaoning, China. Photo by CEphoto, Uwe Aranas, licensed under CC BY-SA 4.0 via Wikimedia Commons.
Raw pasta dough may look uniform, but its constituent starches and proteins aren’t evenly distributed. These variegated molecules help define the pasta dough’s rheology, which describes how it flows and deforms in response to applied moisture, mechanical stress, and heat. Whether it ends up as chow fun or campanelle, the dough’s rheology is affected by how it’s handled at every stage of production.
How Extruders Turn Ingredients Into Noodles
When we make pasta from scratch, we can adjust our dough based on how it looks and feels; add a little more water here, then do some kneading there. When pasta is made on an industrial scale, such hands-on rheological adjustment is no longer an option. A noodle factory uses machines, such as extruders, to mix and knead raw pasta dough. Below is an example of a typical pasta extruder design:
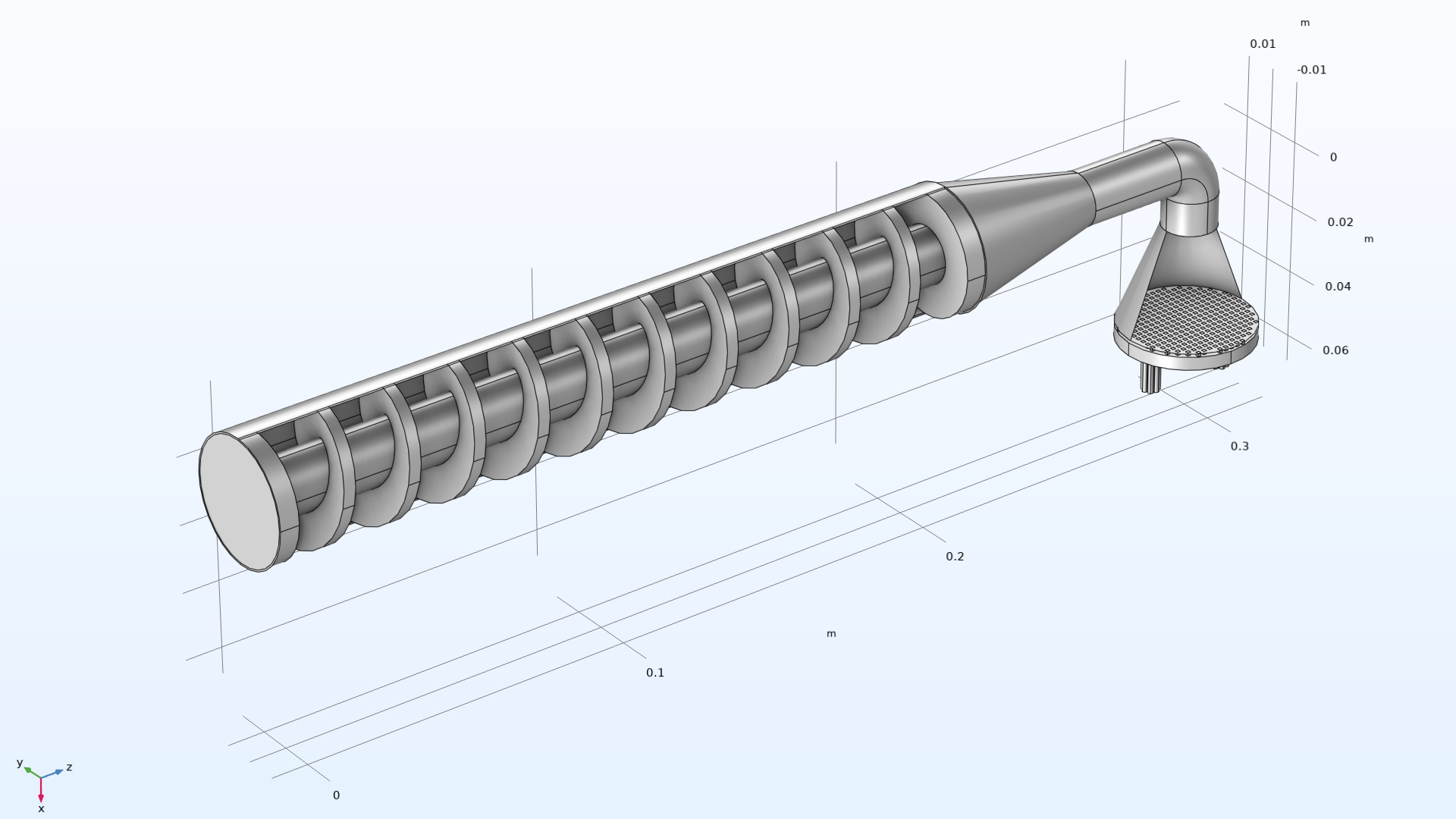
An illustration of the components inside a pasta extruder, as rendered in a tutorial model.
The heart of an extruder is the extrusion screw or worm, which is a rotating shaft combined with a screw-like blade. (It sort of looks like a giant fusilli noodle!) Water and flour are fed into the left side of the pictured extruder design. As the extrusion worm turns, it forces the ingredients toward the right. The heat, movement, and pressure generated by the worm’s motion convert the mixture into dough, which is then pushed through holes in the pictured outlet nozzle on the right side of the machine. Attachments can be fitted to the outlet to create various noodle shapes, and other devices will cut and dry the final product.
The Potential Problems of the Extrusion Process
Even though pasta has been made by similar machines for hundreds of years, the technology is still far from perfect. A study by researchers at the University of Naples (Ref. 2) notes that the extrusion process involves complex “polymerization phenomena, driven by a combination of pressure and temperature.” Problems that can occur inside the extruder include:
- Incomplete mixing of flour and water
- Uneven pressure distribution and extrusion velocity
- Poor circulation of dough, which can allow mold to form
These problems can affect how the final product looks and tastes, or even make it unsafe to eat. To help predict conditions that could cause such issues, we can model the pasta extrusion process using the COMSOL Multiphysics® software.
Modeling the Uneven Distribution of Heat and Velocity
A tutorial model available as of COMSOL Multiphysics version 6.0 shows how to model the nonisothermal flow of dough through a pasta extruder. The model can be used to predict how conditions inside the extruder may affect the final product.
Due to increasing temperature, generated by mechanical agitation, the viscosity of the pasta dough will decrease as it moves through the extruder.
Note: The moisture level is assumed constant in the model for simplicity, and is not described here.
The Nonisothermal Flow, Laminar Flow interface, which provides a coupling between the Creeping Flow and Heat Transfer in Fluids interfaces, enables us to account for this dissipation in viscosity. The movement of the extrusion screw is captured inside a rotating domain at an angular velocity of 20 rpm. A frozen rotor analysis provides a memory- and time-efficient approximation of the screw’s action and the resulting flow field of the dough.
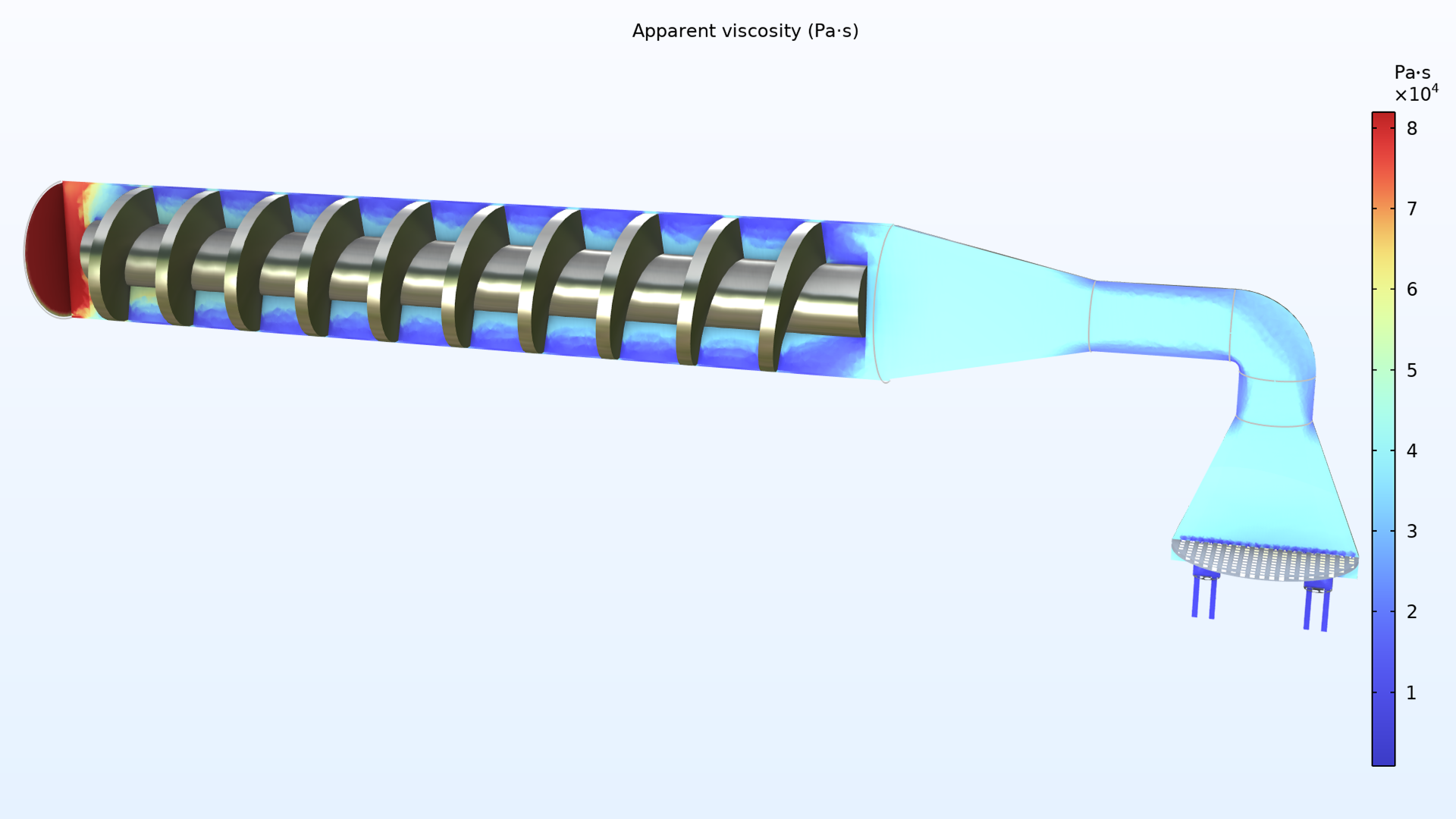
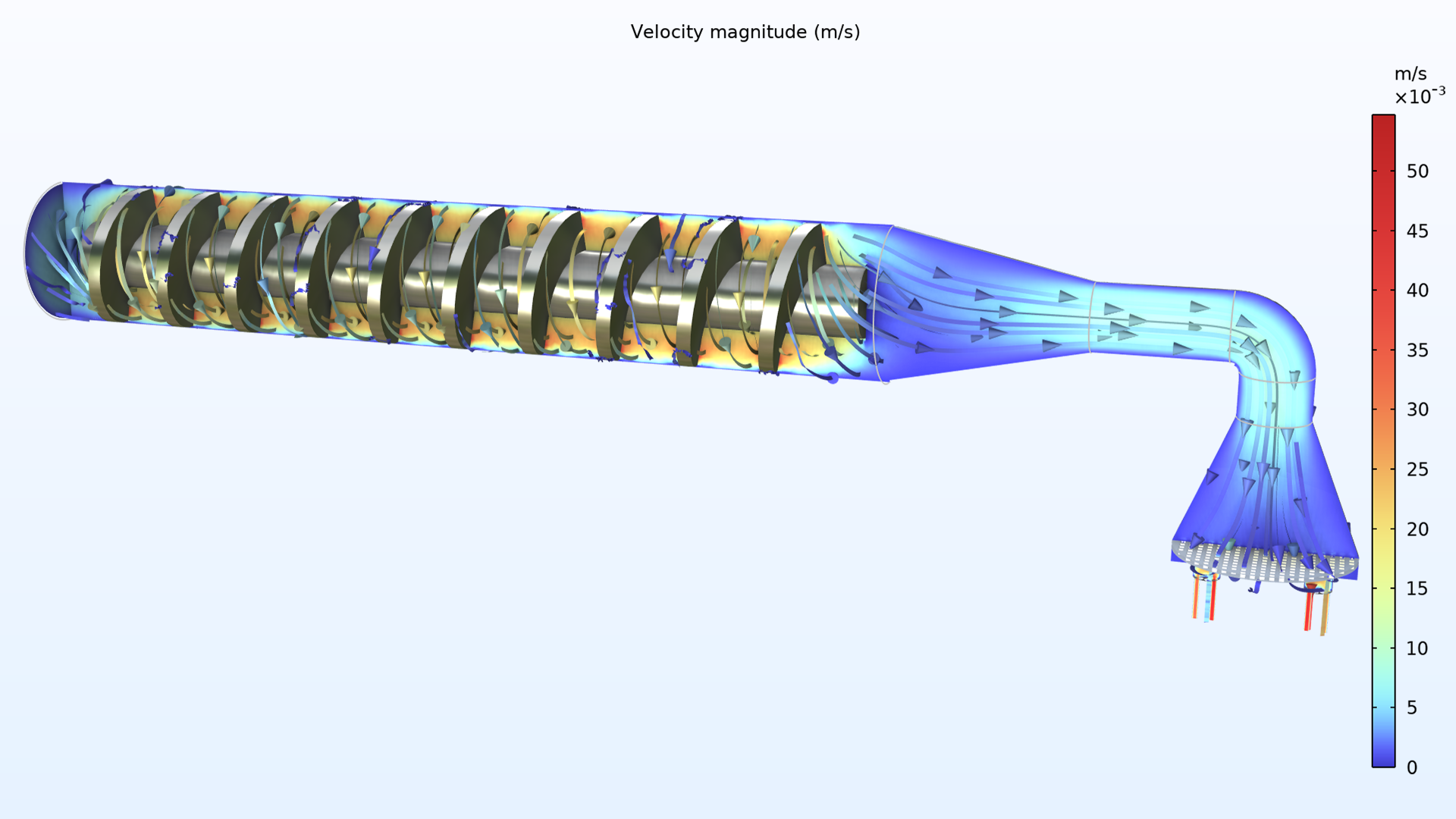
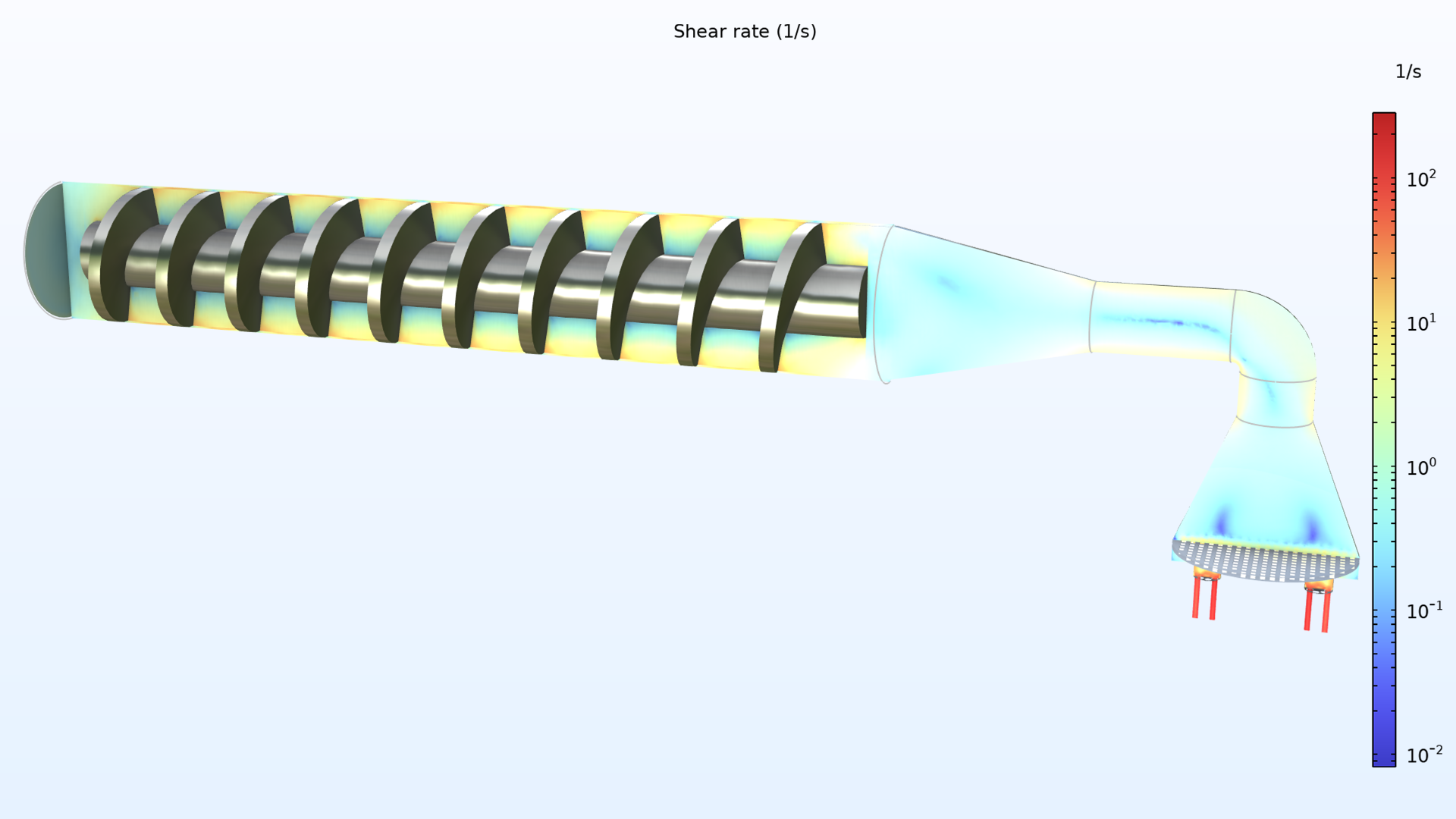
Simulation results from the extruder model show the combined effects of heating and shear stress on the dough. Viscous heating is greatest where the shear rate is greatest, which occurs where the screw surface meets the outer wall. The heat generated near the wall is continuously advected in a helical path toward the extrusion outlet. Since the dough is shear thinning, the viscosity decreases as the shear rate increases. Viscosity also decreases as the temperature increases. These nonuniformly distributed effects lead to a variation of nearly an order of magnitude in viscosity. Parts of the dough close to the middle of the blade, where the shear rate is low, rotate almost like a rigid body. This can lead to very poor mixing perpendicular to the flow, resulting in uneven dough quality.
Simulated temperature profile (left) and apparent viscosity (right) inside the pasta extruder model.
In addition, the dough’s temperature is nonuniform close to the outlet. These simulation results suggest that thermally insulating the extruder would result in a more uniform temperature at the outlet of the screw section, thus ensuring more uniform dough properties before the dough reaches the nozzle.
Simulated velocity profile (left) and shear rate (right) inside the pasta extruder model.
Serve Up Your Own Pasta Simulation
While my grandmother’s pasta might not be available for you to try, the pasta extruder model described above sure is. Download it and try your own simulation via the link below — but if all this pasta talk made you hungry, maybe have some spaghetti first!
Hungry for More Food Science?
Check out these posts that also address the behavior of foods:
- The Science Behind Cooking Caramel
- Finding the Best Way to Make Crêpes with Fluid Dynamics Research
- Can a Wine Cooler Actually Keep Your Beverage Cold?
References
- S. Marchetti, “Chinese Noodles Not The Inspiration for Pasta, Historians Say, Its Roots Are in Ancient Greece — And They Have The Texts to Prove It”, South China Morning Post, 23 Apr. 2020; https://www.scmp.com/lifestyle/food-drink/article/3080891/chinese-noodles-not-inspiration-pasta-historians-say-its-roots
- F. Sarghinia, A. Romano, and P. Masi, “Experimental Analysis and Numerical Simulation of Pasta Dough Extrusion Process”, Journal of Food Engineering, vol. 176, pp. 56–70, May 2016; https://doi.org/10.1016/j.jfoodeng.2015.09.029





Comments (4)
Sohan Birla
February 21, 2022Allan : Great example of using COMSOL for real complex problem. It would be more useful if we can have co-rotating twin screw model
Alan Petrillo
February 22, 2022 COMSOL EmployeeHello Sohan,
Thank you for your comment! I will pass your suggestion on for consideration.
Saeid Kheirandish
March 5, 2022Finally, there is an example in the application gallery featuring an elaborate extruder model. That is great news, especially that here in addition to using a non-Newtonian fluid model under non-isothermal conditions, the flow is not only simulated in the screw region, but also through the die. This is almost as general as an extruder example can be, and it can clarify many questions (regarding e.g. the choice of mesh elements or how to implement the temperature dependence of viscosity) for an interested user.
However, in case of polymer or rubber extrusion, there are certain features of the example that look unfamiliar. Food engineers (who, I assume, are the primary audience for this paper) have a justified obsession with temperature as it has a significant effect on the quality (that is to say, taste, smell, color and the consistency) of whatever they are processing into finished products. If anything goes wrong, they will know immediately because the customers will tell, and this example successfully shows how to predict the development of temperature along the screw and in the die to avoid over- (and possibly) under-heating. The choice of boundary conditions for this example, however, may seem odd to polymer and rubber engineers: the solution to the classical (isothermal) extruder problem dates back to the work of Boussinesq in the 19th century [1] and the first solutions to the non-isothermal case were offered by Griffiths [2] and Zamodits [3]. Countless works have followed ever since to either validate the predictions of these early works with experimental data or attempted to introduce minor modifications to the methods, but the boundary conditions have always remained the same:
(1) fixed mass throughput (or alternatively, given velocity profile) at the entrance to the screw channel
(2) constant wall velocity coming from the rotational speed of the screw, and
(3) zero pressure at the exit
In trying to reproduce the results of a paper on pasta extrusion [4], this example drops the first boundary condition and assumes an open boundary at the inlet with a fixed pressure of 20 bar. This pressure, according to the paper, has been seen to be the experimental threshold for transition from “powdery hydrated semolina” to dough (boundary conditions 2 & 3 remain similar to the classical example and the thermal boundary conditions are also similar to those of literature). Being partial to measuring what can be measured and modelling what can’t, I would rather imagine an extruder operator standing at the die outlet and collecting extrudate samples (then weighing them at known time intervals, then calculating the mass flow rate) than measuring pressure at the point where powder turns into dough.
Another minor peculiarity is the anomalous temperature dependence of the power law exponent: it drops, rises, then drops again with temperature rising from 35°C to 80°C. With polymers, the temperature needs to be high enough to give a melt but not too high to start degradation, and the good news is that, absent any unwanted reactions that are triggered with temperature, the viscosity monotonously decreases with increasing temperature. The authors of Ref. [4] attribute this to complex interactions among dough ingredients at various temperatures. This may of course be a plausible explanation in pasta or cereal production but will remain an abnormality in the broader extruder universe. And yet, perhaps inadvertently, this manages to demonstrate the ease with which temperature dependence of material parameters can be considered in a non-isothermal CFD model, which is just one of numerous unique strengths of COMSOL.
[1] M. J. Boussinesq, J. Mathematique Pures et Appliquees. 13:377-424 (1868).
[2] R. M. Griffith, Ind. & Eng. Chem. Fund. 1:180-187 (1962).
[3] H. J. Zamodits and J. R. A. Pearson, Trans. Soc. Rheol. 13: 357-385 (1969).
[4] F. Sarghini, A. Romano and P. Masi, J. Food Eng. 176:56-70 (2016)
Alan Petrillo
March 7, 2022 COMSOL EmployeeHello Saeid,
Thank you for reading, and for your informative comment! I’m sure other modelers will find it insightful and helpful as well.
Alan