
The acoustic diffusion equation is the quickest and easiest way to model high-frequency acoustics. In fact, this method of acoustical analysis proved particularly helpful in planning the layout of my parents’ future home. I will introduce the topic of acoustic diffusion by sharing my own personal experience, while highlighting the assumptions behind this modeling approach, as well as its strengths and weaknesses.
A Home for Living
My parents love each other to death, but their habits can sometimes clash. My mom enjoys watching late-night television talk shows, while my dad prefers a good night’s sleep whenever he gets the chance. As they will eventually need to downsize, I decided to help them plan a home where they could stay friends.
From past experience, I knew there was no sense in trying to optimize the location of every plant, rug, or bookcase. My dad is constantly moving furniture around to, as he says, “feel the space.” My mom, meanwhile, tends to pull the couch closer and closer to the television rather than admitting that she needs glasses.
In short, they are bound to mess around with the input data and thereby remove digit after digit from the precision of any a priori sound level estimate. Luckily, accuracy was not a primary concern. I just needed to establish that my dad would get his beauty sleep.
Acoustic Diffusion in COMSOL Multiphysics
The obvious start for a “quick and dirty” model of the acoustics in an apartment is the Acoustic Diffusion Equation interface. This interface is very easy to use and, in most situations, it is a lot faster than the more accurate Pressure Acoustics or Ray Acoustics interfaces.
For my simulation, I created a simple drawing of the relevant rooms and included the larger pieces of furniture. With the drawing complete, I set out to create my first acoustic diffusion model. This was a breeze — two power sources representing the stereo speakers connected to the television, absorption coefficients assigned to the walls and the furniture, and…that was it.
Approximate absorption coefficients for common materials are easy to find online. If you want to be more thorough, you can use different values in different frequency bands, or even specify them as arbitrary functions of the frequency. I selected a constant low value for the walls (including the floor and the ceiling) and a higher one for the soft parts of the furniture. To compensate for the lack of carpets and the relatively sparse decoration, I then nudged the wall coefficient slightly in the upward direction. If you decide on a similar time-saving measure, I suggest that you be open about it. My parents understand that acoustic diffusion is not an exact science, and they appreciate my honesty.
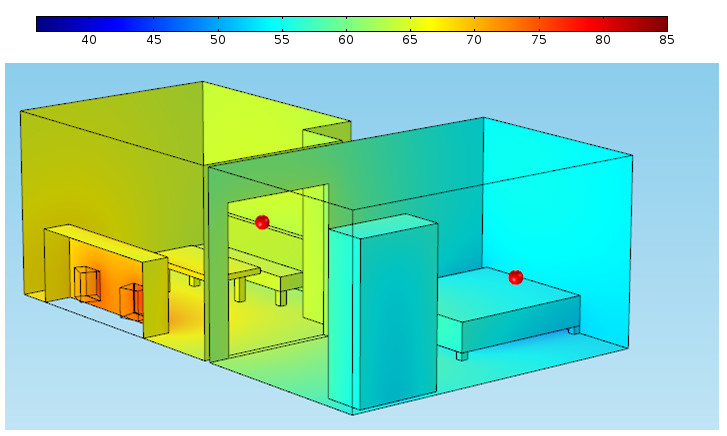
Distribution of the sound pressure level (dB) without a door between the rooms. The red dots indicate my mom’s viewing position and my dad’s head while he is trying to sleep.
A Door and Direct Sound
My first solution shows a sound pressure level decreasing by a quite modest 11 dB between the living room couch and the bedroom. Luckily, two important elements that would increase the difference were still missing.
The first element is a door between the rooms. If your door manufacturer cites a transmission loss in dB, make sure to check whether it concerns only transmission through the door itself, or if it was measured with the door in its frame. This makes a difference because a significant amount of sound may sneak through the space between the door and the floor unless you install a fitting. If you have access to a drawing of the door and know the material that was used to make it, you can, of course, run an acoustic-structure interaction analysis to get a second opinion. It is trivial to include a door with a specified transmission loss in an acoustic diffusion simulation.
The second element is the direct sound. The acoustic diffusion equation only deals with the part of the sound that has already struck the walls or the furniture and has become diffuse. With my mom sitting directly in front of the television, there is also a significant direct sound reaching her. By approximating the sound sources as points and neglecting shadowing from the table, it is quite simple to add the direct sound as an analytical expression in terms of the emitted sound power and the local coordinates.
In my second — and final — simulation, I added the direct sound hitting the couch and put up a door between the rooms. The total loss between the couch and the bed was now a much more acceptable 23 dB. I provided my parents with a nice printed report and gave them the thumbs up to move into the home.
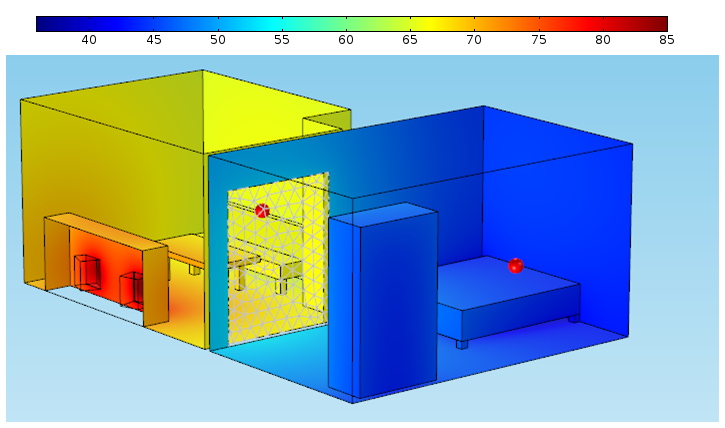
Sound pressure level distribution (dB) with a door added and an approximation of the direct sound included in the living room.
The Acoustic Diffusion Equation
Diffusion is often discussed as a description of the motion of particles in a gas. The particles travel in straight lines except when, at random intervals, they bounce off the gas molecules. The diffusion coefficient is a function of the mean free path between two consecutive collisions.

Mean free path between collisions in a gas (left) and for sound particles in a room (right).
The acoustic diffusion equation deals with conceptual “sound particles”, with a density proportional to the local sound energy. These particles do not bounce on the air molecules, but rather on the walls of the room. The mean free path \lambda and, with that, the diffusion coefficient D relate to the proportions of the room. It holds that \lambda = 4V/S, where V is the volume of the room and S is the total surface area of the room’s walls, floor, and ceiling. In turn, D=\lambda c/3, where c is the speed of sound.
The implementation of the acoustic diffusion equation in COMSOL Multiphysics is
The equation is solved for the acoustic energy density w, from which you can derive the sound pressure level and other important measurables. If you drop the time derivative, you get the stationary form. The volume absorption coefficient m_a accounts for the air dissipation, which is often negligible but sometimes important in very large spaces. D_t = D is the diffusion coefficient and q is an optional volumetric sound source. With the alternative formulation
you can also include an averaged description of the furnishing. Here, \alpha_f is the average absorption coefficient of the furniture (the fittings). The diffusion coefficient D_f and the mean free path \lambda_f derive from the number density and the average cross section of the furniture.
Say, for example, that my parents had wanted to invest in a furniture store. In that case, I would have used this formulation rather than draw each individual item.
The boundary conditions include various ways of specifying the local absorption coefficient and applying sound sources. Point sources are also available.
Strengths and Weaknesses of Diffusion Acoustics
Like ray acoustics, the acoustic diffusion equation does not account for low-frequency behaviors, such as standing waves or diffraction around corners. These are chiefly important below the Schroeder frequency, which you can learn about more in the blog post “Modeling Room Acoustics with COMSOL Multiphysics“. In my parents’ new living room and bedroom, the Schroeder frequencies are 167 Hz and 183 Hz, respectively.
For events to turn into statistics, you need to monitor your system for a while. When compared to ray acoustics, the main limitation in the acoustic diffusion equation is that it does not include early sound. This means that it will systematically underestimate the sound pressure level in the vicinity of the sound sources — the case for my mom’s viewing position right in front of the television. You can take my approach and often at least partially compensate for this limitation by calculating the direct sound analytically and adding it to the diffuse solution. It can, however, become rather difficult or impossible to do so if there are obstacles near the sources acting to reflect or absorb the sound.
While it can be argued that acoustic diffusion is the least accurate of the three acoustics analysis methods available in COMSOL Multiphysics, acoustic diffusion is easier to set up and is often orders of magnitude faster to solve than other methods. The solution time required to produce the plots presented here was approximately 2.5 seconds on a regular desktop computer. For a ray tracing model with a high number of rays, obtaining good statistics would take at the very least a few minutes — and possibly hours — to solve. Pressure acoustics is the only game in town for the low-frequency, resonance-dominated range. But, for frequencies much greater than the Schroeder frequency, this approach would be out of the question due to the quickly increasing solution time and memory usage.
At the end of the day, if your parents ask you for an opinion on the sound environment in their living quarters, I’d wholeheartedly recommend that you run an acoustic diffusion simulation for them. Alternatively, if you are in the early stages of designing a concert hall or an office space, acoustic diffusion can still be a great tool for obtaining an initial assessment of the high-frequency sound distribution. You can then add ray acoustics to predict the early sound and get a more accurate result, as well as pressure acoustics to investigate the low-frequency behavior.
Tutorial Downloads
The simulation referenced in this blog post is available for download here. To learn more about room acoustics, I also encourage you to download the One-Family House Acoustics tutorial from our Application Gallery.



Comments (0)