
Electroplating is commonly used for surface finishing due to its effectiveness across the automotive, electronics, corrosion protection, aerospace, and defense industries. Since WWII, the number of patents claiming to achieve “perfect plating” has increased exponentially. The focus of the narrative surrounding electrochemical plating has also shifted from complex chemical reactions toward perfecting operating conditions. In this blog post, we show how to achieve smoother metal surfaces during reverse pulse plating (RPP) using the COMSOL Multiphysics® software and add-on Electrodeposition Module.
What Is Reverse Pulse Electroplating?
Electroplating involves immersing metal electrodes in an electrolyte bath and then applying an external current over the electrodes. At the cathode, we obtain a reduction of the ions in the bath, forming a metal coating. The anode can either be a dimensionally stable anode, where oxygen evolution or chlorine evolution occurs, or an electrode that dissolves anodically (which is also known as stripping), where the electrode is oxidized so that the metal goes into the solution as ions.

A model of decorative electroplating on a furniture fitting.
In electroplating, typically either a direct current (DC) or current pulse(s) can be applied. Pulsed-current techniques involve the application of a forward current for a certain time interval with either a short, high-current reverse pulse or zero-current periods interposed. These current pulses are also known as duty cycles. For the RPP process, current pulses of equal or varying amplitude, duration, and polarity are used to combine electroplating and stripping.
RPP is composed of a forward duty cycle (t_{fwd}), at which a cathodic current is applied and the deposition of metal takes place (plating), and reverse duty cycle (t_{rev}), during which the plating current is reversed for the dissolution of metal ions to take place (stripping). In each direction (forward and reverse), the duty cycle is defined as a ratio of the plating/dissolution time to the total time of the applied current. The average current density with respect to the duty cycle is given by:
where t_{fwd} and t_{rev} are the forward and reverse duty cycles and hold the relation t_{rev}+t_{fwd}=1.
By optimizing both the electroplating and the stripping processes, through controlling the duty cycles, RPP allows the preparation of smooth coatings. For a constant average current density (i_{avg}) and dissolution current density (i_{rev}), the plating current density i_{fwd} can be defined as:
Quantifying the Current Distribution
According to IUPAC definitions, secondary current distribution is valid when the influence of the activation overpotential cannot be neglected but concentration overpotentials are negligible. When the activation overpotential is included, a high local current density introduces a high local activation overpotential at the electrode surface, which causes the current to naturally become more uniform. (For more information, you can read these blog posts on the theory of current distribution and on how to choose between the current distribution interfaces.)
The secondary current distribution is often analyzed in terms of the Wagner number (Wa), a dimensionless quantity given by:
where \kappa is the conductivity of the electrolyte bath; d\eta/di is the slope of the overpotential-current curve under the above conditions; and \ell is a characteristic length of the system (for instance, the length of the electrode). The Wagner number can thus also be seen as the ratio between primary current distribution effects (via \kappa/\ell, which is influenced by the geometry and electrolyte properties) and secondary current distribution effects (via d\eta/di, the kinetic polarization).
At the Tafel limit or high (anodic or cathodic) overpotentials, Wa becomes inversely proportional to the current density for the process:
where \beta is the Tafel slope.
A higher Wagner number essentially means that the primary current distribution effects are superseded by the secondary current effects, resulting in a more uniform current distribution. Alternatively, for geometries with peaks and recesses, a leveling effect could be achieved by using the primary current density distribution around the working electrode. In the following case, we will see how to use RPP to achieve a better surface finish at a geometry with a given protrusion.
Modeling RPP with COMSOL Multiphysics®
The Pulse Reverse Plating model in the Application Gallery uses the Secondary Current Distribution interface to account for activation overpotentials (reaction kinetics) together with primary current distribution effects (geometric effects and electrolyte conductivity).
We set up a simple 2D geometry with a small protrusion that acts as a site of interest for the shape evolution when subject to different applied current forms (see the image below). The 2D model simulates a copper substrate with a protrusion exposed to an electrolytic bath of finite conductivity. It is assumed that the electrochemical cell consists of a well-stirred electrolyte with constant conductivity (with no concentration gradients); electrodes; and an anode and cathode, where the ohmic losses are neglected.
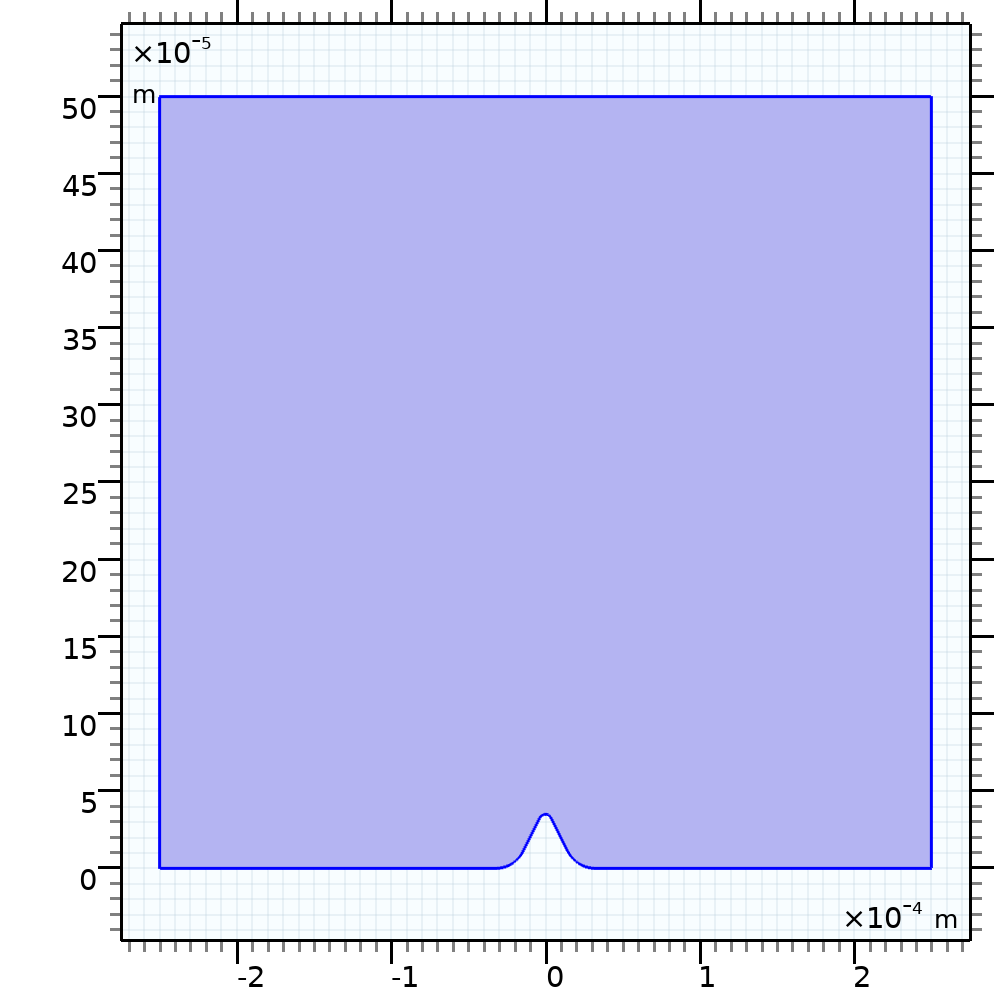
2D geometry used to set up the electroplating model.
To act as a reference for the RPP process, we first set up and solve a model for DC plating.
The electrolyte bath has the conductivity \sigma_l and is set to a domain where Ohm’s law dictates the current density in accordance with:
At the electrode-electrolyte interface, the local current (i_{loc}) is given by:
where i_{loc} is given by the Butler-Volmer equation:
where i_0 is the exchange current density; \alpha_{a,c} is the transfer coefficient; \eta is the overpotential; F is Faraday’s constant; R is the gas constant; and T is the temperature.
The above equation defines the charge transfer kinetics at the interface. When these two processes are accounted for, namely Ohm’s law and the charge transfer kinetics, the analysis is referred to as secondary current distribution.
Current is applied to the boundary surface for the counter electrode. At the plating surface, a redox reaction with known kinetic parameters (reaction rate constants) takes place. The local growth velocity on the electrode surface is then based on the time-averaged sum of the local current densities during the forward and reverse pulses. At any instant during the plating process, each point of the electrode surface advances proportionally to the local current density and in the direction normal to the electrode surface:
where M_{\textrm{Cu}} is the molar mass, R_{\textrm{Cu}} is the rate of mass deposition, \rho_{\textrm{Cu}} is the density, and \nu_{\textrm{Cu}} is the stoichiometric coefficient of the deposited copper.
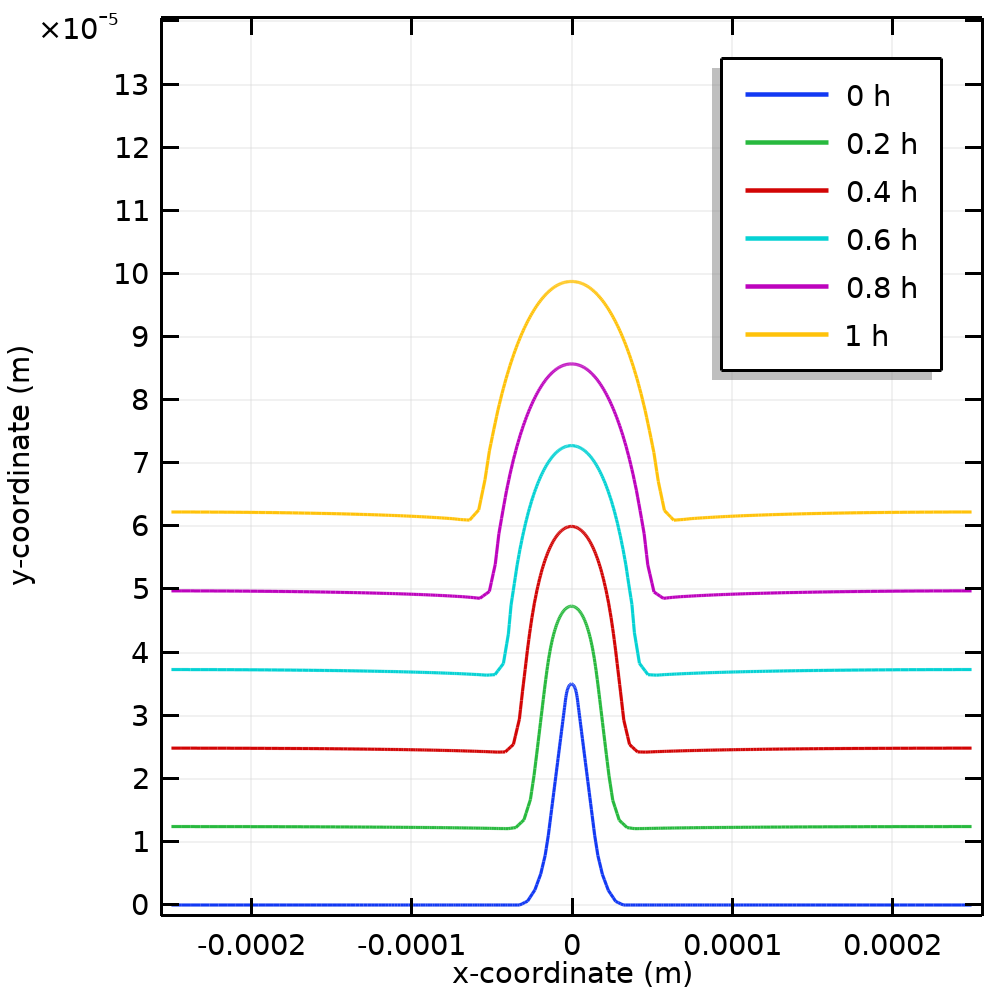
Surface profile evolution versus arc length when using a DC pulse for electroplating.
A time-dependent study is set for an hour to observe the electrode shape evolution for the prescribed current distribution conditions in the DC plating scenario. The figure above shows how the protrusion becomes deeper and wider during the DC plating process.
How Does a Reverse Pulse Benefit the Electrochemical Plating Process?
In RPP, operational parameters such as the current density and the pulse width are crucial to achieving desirable results. The average current density at the working electrode is related to the ratio of duty cycles via Eq. 1. Thus, the plating process can be fine-tuned through the choice of operating cycle parameters. We now proceed to compare the results for the DC and the RPP mode.
We set up the model for RPP by modifying the Electrolyte Current node in the existing study to i_{fwd} (to define the forward pulse for plating) and by introducing an additional Secondary Current Distribution node to define the superimposed reversed pulse for dissolution (stripping). In the second Secondary Current Distribution node, we set the electrolyte current as i_{rev} for the reverse pulse while keeping the kinetic parameters identical to those of the previous study.
The average electrolyte current is kept constant while only varying the pulse width using t_{fwd}; i.e., the forward duty cycle. The plating current densities at the cathode surface are then predicted via Eq. 2 and influence the shape evolution via Eq. 8. We compute the time-dependent study for an hour to get the surface profile for a pulse-reversed current.
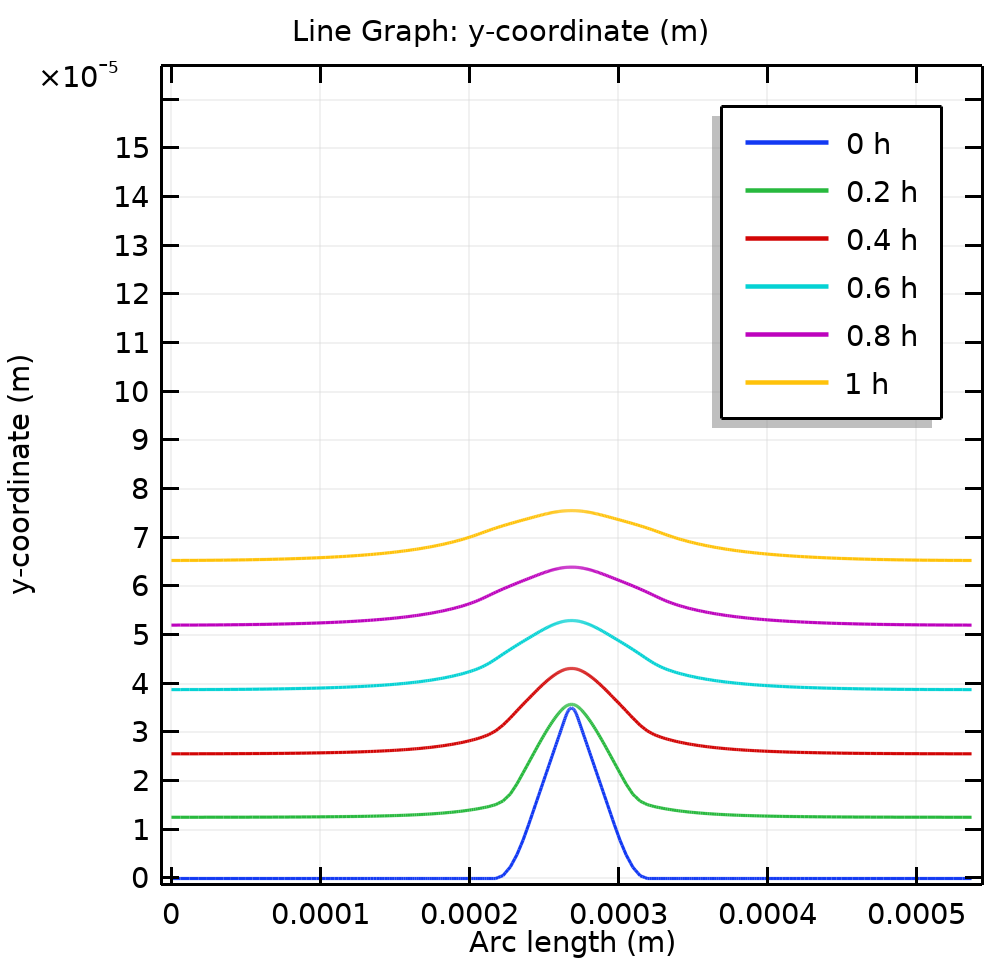
Surface profile evolution versus arc length using RPP for a duty cycle of 0.85.
As shown above, the surface profile shows a more buffed metal surface than for the DC plating using the same average electrolyte current. The study illustrates the application of pulsed currents to achieve the optimal current distribution around the electrode surface. Using a pulsed current density at the electrode surface gives a smoother surface profile without using any electrolytic bath additives, thus reducing the cost and toxicity associated with additional chemical additives.
The Wagner number ( Wa) for a plating process is always smaller when using a pulse-reversed process than with DC, as we get higher instantaneous plating current densities (see i_{fwd} in Eq. 2). This indicates sensitivity to the geometrical features; hence, the localization of the current distribution is enhanced while using pulsed-reversed current. We now try to exploit local current distribution to yield a leveled surface by tuning the ratio of forward and reverse pulse.
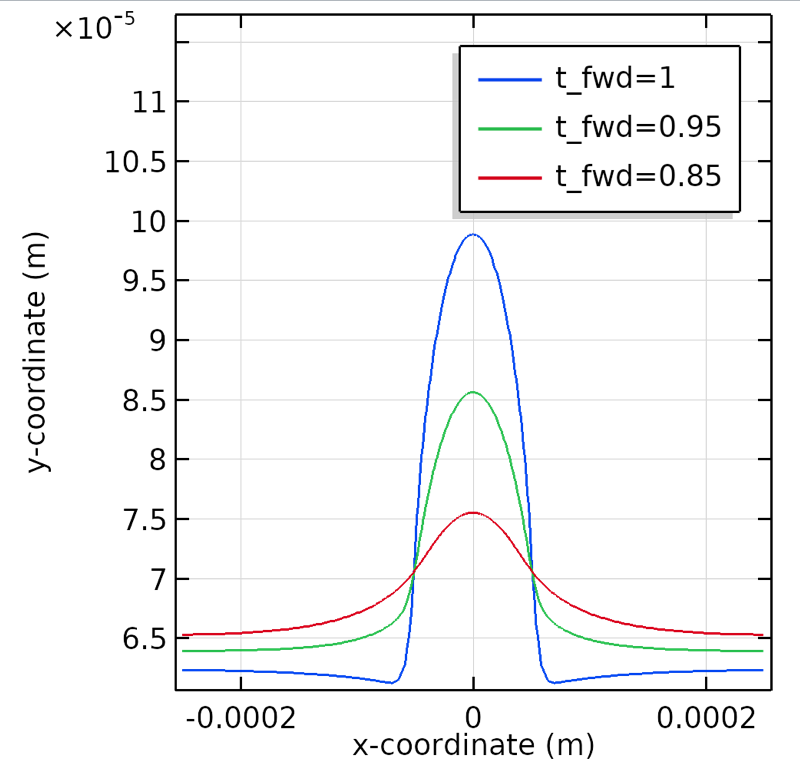
Surface profile evolution versus arc length using RPP for different duty cycles.
In the plot above, we see the continued furbishing effect of attenuating the ratio for the forward and reverse duty cycles for reverse-pulsed current. For RPP, increasing the reverse duty cycle (t_{rev}) increases the dissolution time and the overall current distribution becomes more uneven, leading to different plating rates on the evolving surface profile. During this increased dissolution period, the peak is recessed due to a prolonged dissolution reaction at a higher current density, as ohmic effects dominate the dissolution process. As we decrease t_{fwd}, the ohmic losses become larger relative to the activation losses during both the plating and reverse cycles, leading to a geometry-sensitive, instantaneous current density distribution. This current density distribution, obtained via varying the duty cycles, makes the surface smoother and yields geometric leveling of the protrusion relative to the thickness of the plating.
Concluding Remarks
We have discussed the role of using current pulses instead of additional chemical additives to seek operating conditions for the plating current in order to make the plated surface as smooth as we can afford. For a system with known kinetic parameters, the Wagner number is inversely proportional to the current density and can be adjusted accordingly to achieve the desired plating on a surface. If we want to fill out the crevices or recess the peaks, we should aim for a system with a lower Wagner number, as in this case. When a uniform coating thickness is required on the surface, we should have high Wagner numbers for the plating process. Current pulses with the smaller forward duty cycle used for RPP result in a lower Wagner number, hence buffing out small protrusions and defects. This is the art in the science of electroplating: to tune the operating conditions without really affecting the chemical composition of the electrolytic bath and eliminating the need for chemical additives.
The model demonstrates the following features:
- Smoother surface profiles are obtained for RPP than for the DC plating process
- The choice of pulse width in RPP can significantly alter the current distribution at the working electrode
- Smoother finishes can be obtained by tuning the ratio of forward and reverse duty cycles
By tuning the operational parameters, simulation can help us understand the advantage of using an RPP technique with respect to DC plating for identical electrolytic baths. Simulation thus provides a tool to minimize the use of chemical additives, toxicity, cost, and maintenance. RPP offers better metal distribution and leveling effects than DC plating for chemically equivalent electrolytic baths.
Next Steps
Learn more about how to simulate the RPP process in COMSOL Multiphysics. Click the button below, which will take you to the Application Gallery with the MPH file.
You can also check out the Electrochemical Polishing model, which is defined using the Electric Currents interface for a 2D geometry.




Comments (3)
Larry Mickelson
November 19, 2018Thanks for this excellent blog post showing the how and why of reverse pulse plating. I especially appreciated understanding that as I’ve worked in similar areas before. Two comments:
1) I think a small math error crept into your equation 2 as i_fwd is shown on both sides of the equation and i_avg is missing
2) Depending on the duration of the pulses, capacitive effects (such as double-layer charging) may or may not consume a significant portion of the total current. Is there a way to incorporate capacitive effects into such a model?
Thanks,
Larry Mickelson
Shruti Srivastav
November 22, 2018 COMSOL EmployeeThanks Larry for your comments. Its always great to see that content we post is helpful to our readers. Regarding your comments:
1) Thanks for pointing out the typographical error. We have corrected it.
2) We understand that double layer is an intrinsic part of all electrified interfaces. You can always incorporate the double layer effects in COMSOL for all Electrochemistry modules. You simply have to right click on the domain features like Porous Electrode or boundary features like Electrode Surface and add the double layer contribution. Hopefully this is useful for you. If you need further assistance with this, please write to us at the support.
Best Regards,
Shruti
Nguyen Kim Thanh Phong
February 25, 2023Thanks for posting your valuable thoughts with us.