
Finland is the home of the sauna; in fact, the word “sauna” is Finnish and is used in English and other languages for what is typically a small room designed as a place to experience heat. In addition to being popular in Finland, saunas are enjoyed in many parts of the world. Classical saunas provide a dry heat that may reach or exceed 100°C (212°F) using an electrical or wood-fired stove. In this blog post, we will explore the heating and temperature distribution in such a sauna using a model created with the COMSOL Multiphysics® software.
The Physics of a Sauna
When using a dry sauna, a stove heats up a small room that is most often covered in wood (aspen, cedar, or pine, for example) and equipped with at least two wooden benches at different heights. Because heated air expands, its density is lower, so the hottest parts of the sauna are close to the ceiling. If you want to experience a more moderate heat, you can use one of the lower benches so that you are closer to the floor.

A classical sauna.
The top of the stove is typically covered with stones (sauna rocks), which increase in temperature and radiate heat to the room. The stones play an important role, absorbing and keeping the heat. You can also add water to the hot stones (as is common in Nordic countries), thereby releasing steam. This increases the humidity and causes an intense heat sensation for a short period of time on the human skin, which stays at a temperature below the dew point. However, it’s only possible to enjoy really hot saunas (up to and beyond 100°C) for more than a couple of minutes if the heat is dry. With dry heat, more moisture can evaporate from the skin, preventing the body from overheating.
The physical phenomena occurring inside of a sauna primarily involve heat transfer and fluid dynamics: heat transfer occurs by convection and radiation, and the heat convection is driven by the movement of the air caused by ventilation and buoyancy forces. A sauna room typically contains air inlets and outlets for the air to circulate. In a wet sauna, moisture content and the humidity are also important physical properties, but in this blog post we will focus on a dry sauna and its heating and temperature distribution.
There are many different types and sizes of sauna stoves, their use depending on the size of the sauna room, for example. Their power typically varies between about 5 kW for use in small home saunas and up to 20 kW for large commercial saunas. In some cases, a wood-fired sauna stove can produce a higher heating power than an electrical sauna stove. However, the actual heating power of a wood-fired sauna stove depends on the quantity, type, and quality of the wood that you use for the fire. Modern electrical sauna stoves include thermostats so that the temperature can be kept at an ideal value.

A sauna stove.
The following properties of the heating process are of interest:
- The time it takes from when the sauna stove is turned on or lit, up to the point where the sauna reaches the desired temperature. If you know how long it will take, then you will know how much time you have to get ready for the sauna experience.
- The heat distribution in the sauna room, especially at the bench levels. This makes it possible for users of the sauna to find a temperature that is pleasant.
Modeling the Heating of a Sauna
As the baseline for the model, we have made some measurement for the blog author’s home sauna, which happens to have a wood-fired stove and no thermostat. It usually takes about 35 to 40 minutes after lighting the wood fire (at normal room temperature) until the temperature reaches about 70°C (158°F) at the top bench.
The Sauna Model
A physical model of the heat transfer in a sauna is a multiphysics model in nature. It includes the following types of physics in the model domain (the air inside the sauna, the sauna stove, and the sauna walls):
- Heat transfer in the fluid (air): This is the temperature field in the air inside of the sauna. It includes the main physical quantity for the model, the air temperature.
- Turbulent flow: This is the air moving inside the sauna. It’s the driving force for the convective heat transfer. It computes the velocity field for the air using a turbulence model.
- Surface-to-surface radiation: This is the thermal radiation from the stove and the sauna walls (that is, transfer of heat by electromagnetic waves), contributing to the overall temperature in the sauna. This computes the surface radiosity, which is the heat radiation from a surface in W/m2 (SI units).
The following boundary conditions are also included:
- An air outflow. For ventilation, saunas usually include a small outflow of air to the outside of the building.
- An air inflow. Saunas also include some air inflow from ventilation or some opening to a surrounding room.
- Heat flux through the walls. The heat flux through the walls will vary depending on the type of wall and the surrounding temperatures. Most often, sauna walls are covered with wooden panels, but part of it can also be pure concrete walls. Sometimes, at least one wall is an external wall, where the air on the outside can be significantly colder (for example, during winter months in Nordic countries). In this model, separate Heat Flux — Outside and Heat Flux — Inside nodes are used to take the colder external temperature (10°C; 50°F) into account. The inside temperature is set to 20°C (68°F).
- A boundary heat source at the top of the heater (sauna stove), where a 10 kW heating power is used, but with a heater startup time of 10 minutes. The expression for this boundary accounts for a thermostat that will turn off the heater if the average temperature at the ceiling reaches 100°C, but in this sauna model, and in reality, such a high temperature is not reached.
The model will have to take all of these physics into account, using material properties and knowledge about the properties of the sauna stove, the dimensions and placement of the overall sauna interior, and the stove and benches. When that information is available, you can start setting up a sauna model using COMSOL Multiphysics and the Heat Transfer Module, which is needed for modeling turbulent flow and surface-to-surface radiation.
Creating the Model in COMSOL Multiphysics®
Setting Up the Model
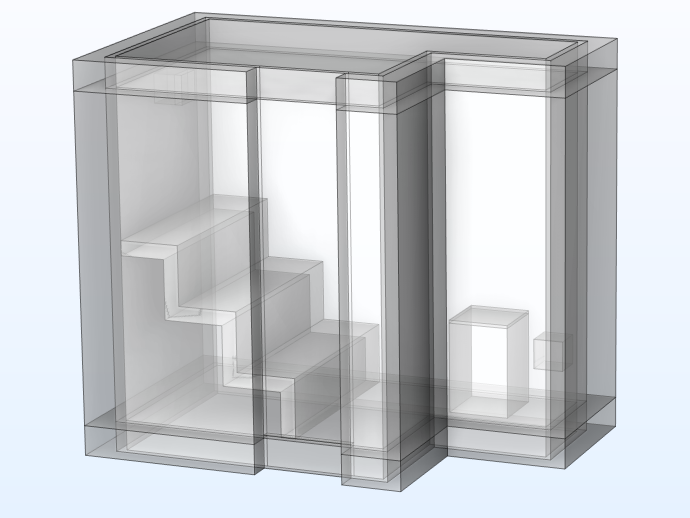
The first step is to create a 3D geometry representing the interior of the sauna and the surrounding walls, i.e., the outer bounds of the model. The 3D sauna geometry with the sauna stove, benches, and air inlet and outlet looks like this:
The sauna geometry with the ceiling and door hidden from view. The heater and inlet are located to the right, and the benches and the outlet to the left. The left wall is an outside wall; the other walls are internal.
A Domain Point Probe feature is defined at a point on the back wall, where a sauna thermometer is located, to visualize the rise in temperature at the position of the thermometer during the transient simulation.
Interfaces
The COMSOL Multiphysics model must implement all the abovementioned physics. This is accomplished with three physics interfaces. The first is the Heat Transfer in Solids and Fluids interface, used for including the heat transfer by convection in the sauna, where the walls are solids and the air inside the sauna is the fluid.
The second interface, used to account for the turbulent flow of air inside the sauna, is the Turbulent Flow, Algebraic yPlus interface. It uses the algebraic y+ turbulence model, an algebraic turbulence model based on the distance to the nearest wall. The algebraic y+ turbulence model uses Prandtl’s mixing-length theory and is suitable for modeling internal flows.
Lastly, the Surface-to-Surface Radiation interface should be used to implement the radiative heat transfer between the stove and wall boundaries (the interior air does not significantly participate in the radiative heat exchange).
Nodes and Materials
Two multiphysics feature nodes take care of the coupling between the air flow and the heat transfer (nonisothermal flow) and the coupling between surface-to-surface radiation and the heat transfer in the air. One is the Nonisothermal Flow node. This node connects the Turbulent Flow, k-ε and Heat Transfer in Fluids interfaces to model fluid flows where the fluid properties depend on temperature. The other node is Heat Transfer with Surface-to-Surface Radiation. It connects the surface-to-surface radiation from the walls and the convective heat transfer in the air in cases where you want to account for heat transfer by radiation on boundaries and where the surrounding medium does not participate in the radiation.
In addition, the following four materials are used in the model:
- Air, which contains temperature- and pressure-dependent material properties for the air (and is included in the built-in material library)
- Concrete, which is the material used in the sauna walls
- Wood (pine), which is the material that covers the interior parts of the sauna walls, and is also the material used for the benches
- Radiating walls, which is an extra user-defined material that is used to define the surface emissivity on the boundaries
Outflow and Inflow nodes are added to represent the inflow and outflow of heat, respectively. Also, a Heat Flux node is active on the wall boundaries for adding a heat flux defined by the external temperature and the heat transfer coefficient. Finally, the sauna stove is modeled using a Boundary Heat Source node. To model the heating process, an expression is used, which includes a thermostat that turns off the heater if the temperature exceeds 100°C and a smooth startup phase that lasts around 10 minutes. The expression used for the boundary heat source is 10[kW]*flc2hs(100[degC]-aveop1(T),10)*flc2hs(t-t_heater/2,t_heater/2), where the first factor, 10[kW], represents the nominal heating power of the stove. The second factor uses the built-in function flc2hs, which is a smoothed Heaviside function with a continuous second derivative without overshoot, to ensure that the heater turns off if the average ceiling temperature approaches 100°C. In the example given, this temperature is not reached, so the second factor is equal to 1. Finally, the third factor, flc2hs(t-t_heater/2,t_heater/2), provides a smooth startup around t_heater, with the smoothing lasting t_heater/2 before and after the start time. The following plot shows the heat power versus time:
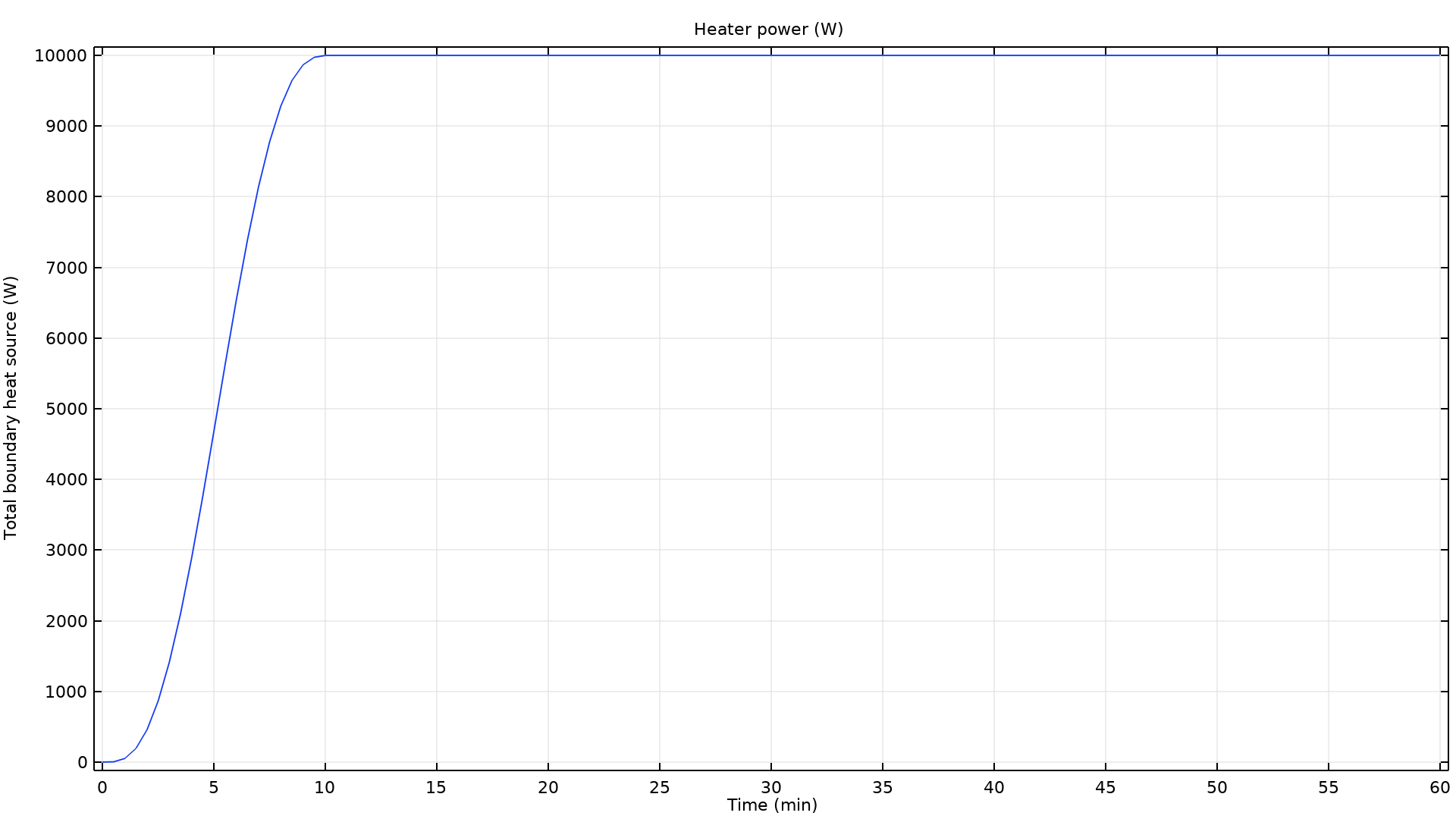
The heater power rises from zero to its nominal value of 10 kW in about 10 minutes.
Studies
There are three studies for the model. The first is a stationary study with initialization. It includes a Wall Distance Initialization study step, used with turbulent flow for computing the reciprocal wall distance, as well as a Stationary study step, which computes a stationary starting solution for the air flow. The Heat Transfer in Solids and Fluids and Surface-to-Surface Radiation interfaces are not active in this step.
The second study contains the main Time Dependent study step. This includes the three physics interfaces and two multiphysics couplings mentioned previously. In the settings for the Time Dependent study step, minutes are used as the time unit, and the output times are set to range(0,0.5,60), a COMSOL Multiphysics expression for outputting the solutions every 30 seconds for one hour. (The actual time steps taken by the solver are controlled by tolerances and are independent of the chosen output times.) Rather than starting from a zero velocity, the computation starts with the velocity field obtained from the first study, which calculated the initial velocity field caused by ventilation. This study step takes about 45 to 55 minutes to compute on a good computer. During this time, you can monitor the airflow and temperature in the domain as well as the temperature at the position of the sauna thermometer using the plot-while-solving and probe functionality in COMSOL Multiphysics.
The third study is added as a convenience. It contains two Study Reference nodes, one referring to Study 1 and the other to Study 2. So, by running the third study, you run the first two studies in a sequence.

The three studies in the sauna model: the first for the wall distance initialization; the second for the time-dependent simulation; and the third for conveniently running both of them.
Temperature Distribution Results
The main result we are looking at is the changes in the sauna’s temperature after 60 minutes. The results can be seen in the slice plot below:
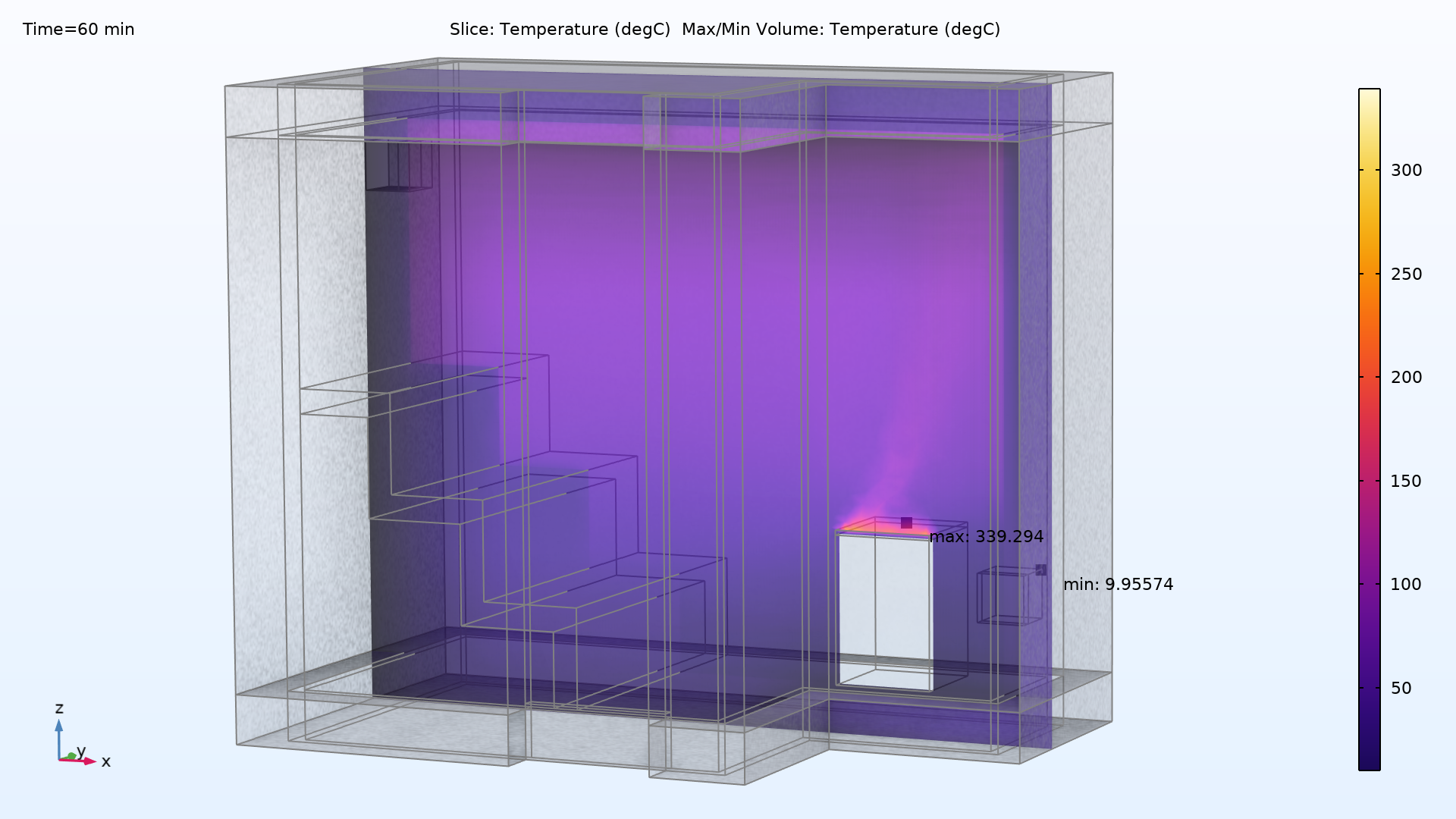
The temperature distribution in the sauna after 60 minutes of heating. The maximum temperature, 339°C (642°F), is at the top of the heater, whereas the air inlet remains at the outside temperature of 10°C.
To get a better view of the vertical temperature differences in the sauna, you can limit the data and color ranges to only show temperatures between 10 and 100°C. The following plot shows that there is a significant temperature gradient from the floor to the top bench:
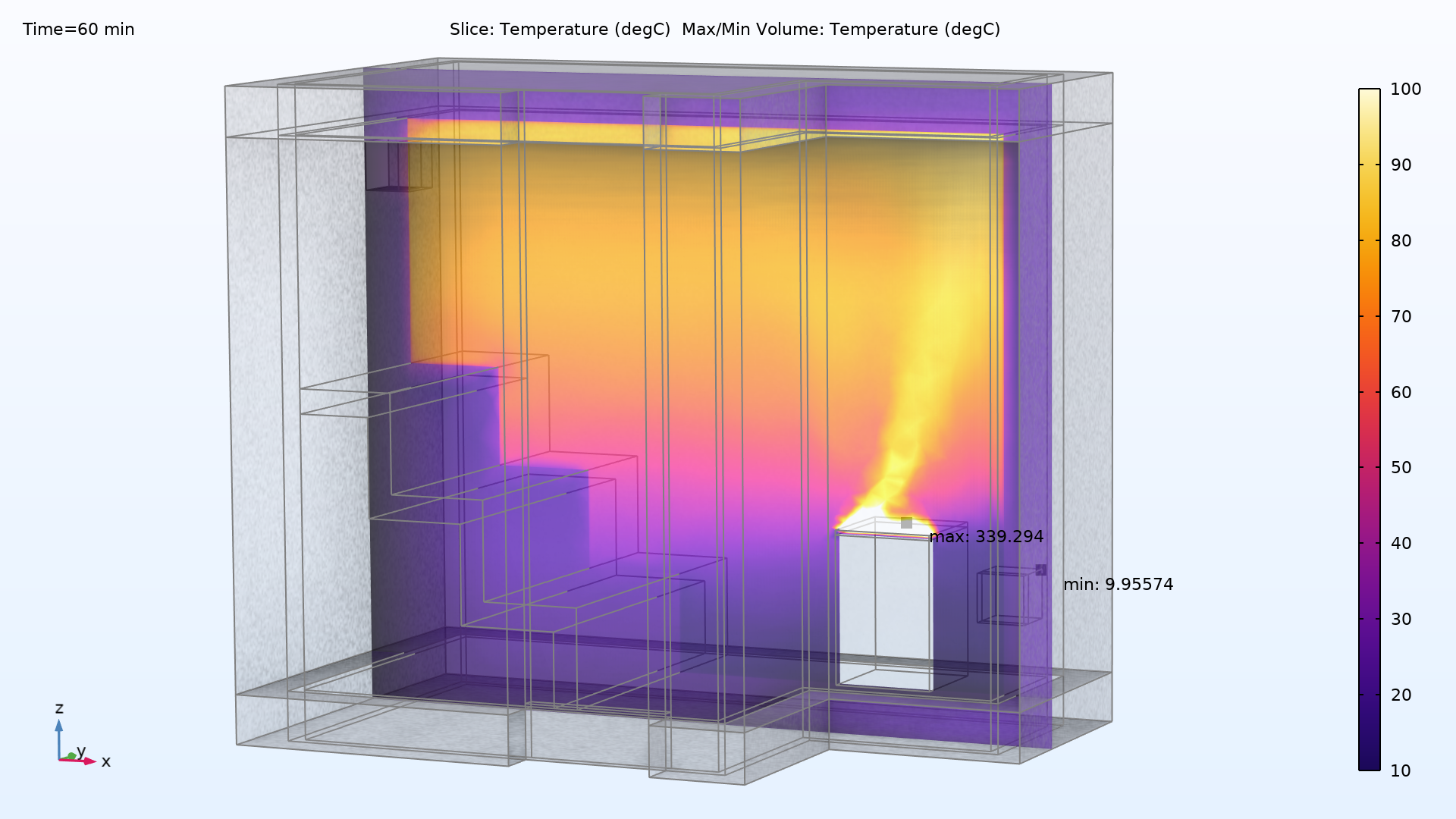
This plot shows that the temperature is around 70°C at the top bench, but only 30–40°C (86–104°F) at the bottom bench, so you can avoid excessive heat by moving to a lower position, if you want.
A line graph of the temperature from the Domain Point Probe feature shows how the temperature increases at the point where a sauna thermometer is mounted:
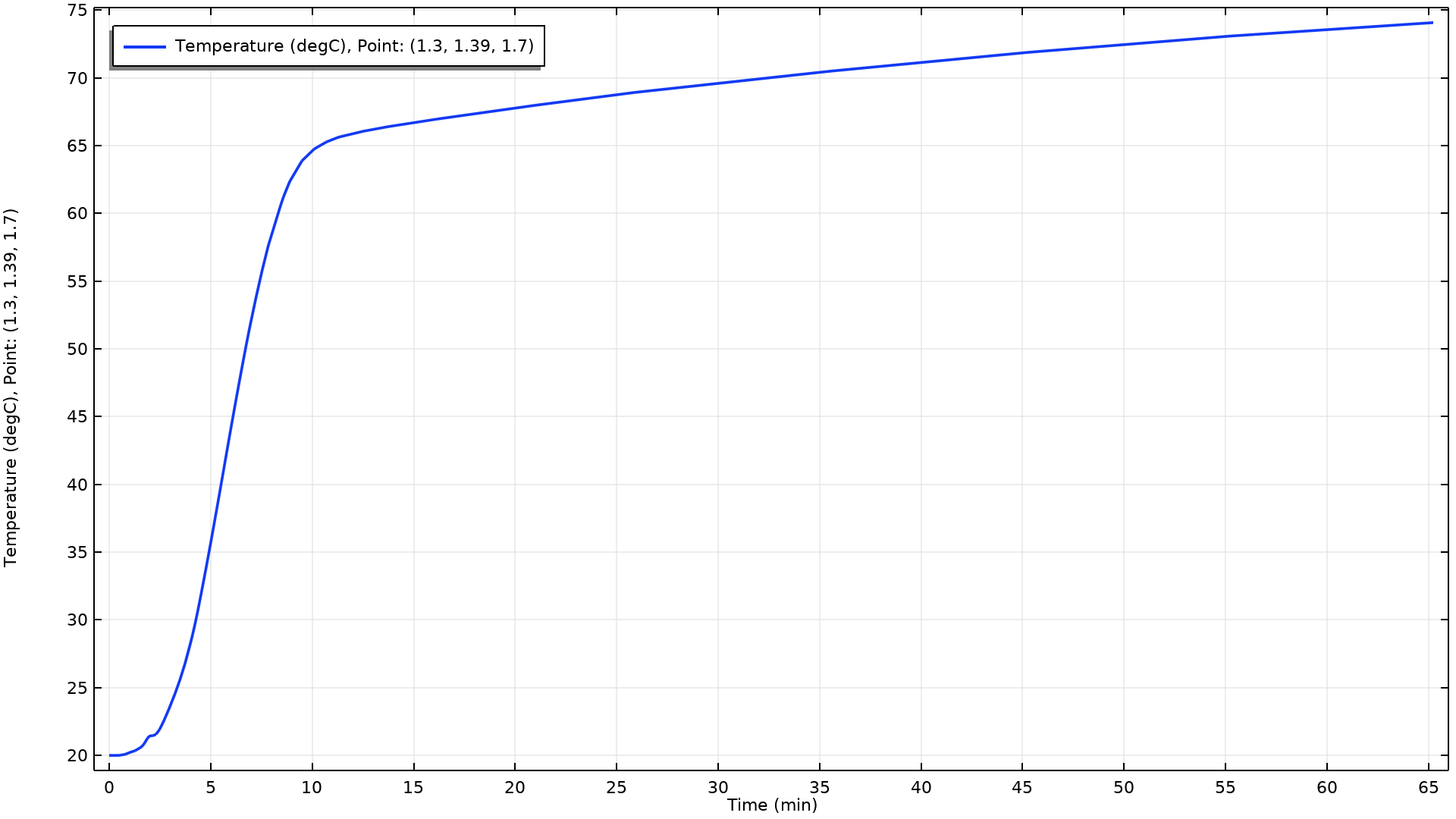
The temperature versus time at the location of the sauna thermometer. The temperature rises fairly quickly, but if you want to have a temperature of 70°C before enjoying the sauna bath, you will have to wait more than 30 minutes, which matches the author’s own experience.
To further explore this multiphysics model, you can experiment with varying stove heating power, ambient temperatures, material properties, bench locations, and other parameters that can influence the heating and temperature distribution in a sauna.
Concluding Remarks and Further Reading
This blog post demonstrates how COMSOL Multiphysics models can be used to explain and explore the heating of a sauna. Similar types of models can also be used for heat and moisture transport (HAM) modeling to improve and optimize the heating of buildings in general and for other heating applications. Take a look at the following examples of building heat-based models using COMSOL Multiphysics and the Heat Transfer Module:
- Heat Transfer in a Room with a Stove: This model shows the intensity of stove radiation on different surfaces of the room.
- Thermal Bridges in Building Construction — 3D Structure Between Two Floors: This example corresponds to case 3 described in the European standard EN ISO 10211:2007 benchmark case for thermal bridges in building constructions.
- Condensation Risk in Wood-Frame Hall: This 2D stationary model computes HAM transport in a wall composed of different hygroscopic materials.
- Heat and Moisture Transport in a Semi-Infinite Wall: The HAM model is defined as a benchmark case in norm 15026:2007 annex A.





Comments (4)
Muhammad Kashif
January 10, 2024Hi Magnus,
Thank you for a wonderful blog about heat transfer!. Is it possible to get the COMSOL file for this simulation?
Best
Kashi
Magnus Ringh
January 11, 2024 COMSOL EmployeeHi Kashi,
Thank you for your kind words. Please contact your local COMSOL office about getting a model file.
Best regards,
Magnus
Ilkka Veuro
March 1, 2024The sauna room is quite a small for 10 kW heating power. And the sitting benches should be open as in picture “the classic sauna”. In wood warmed saunas there is no thermostat and 10 kW electrical stove is too much for this small sauna room.
Magnus Ringh
March 4, 2024 COMSOL EmployeeHi Ilkka,
Thank you for your feedback. It’s hard to say what a correct power would be here. It’s easy to make parametric studies to vary the power and modify the geometry if desired.
Best regards,
Magnus