
Multiphysics applications are all around us. Consider, for example, a setting where science may be the last thing on our minds: a music concert. You might be enjoying the slight sinusoidal variations in atmospheric pressure we call sound waves, or music, but those pressure variations must come from somewhere. In fact, they are due to a multiphysics effect where sinusoidal structural vibrations in an object disturb the surrounding air, causing pressure variations in the air that then propagate outward and create the sound waves your ears recognize as music. When it comes to tuning an orchestra to produce perfect sound, we can get help from a multiphysics simulation.
Tuning an Orchestra
In order to determine the sound produced by an object, you must know all of the structural qualities of that object. Conversely, in order to understand the structural behavior of an object, you must take into consideration the properties of the fluid (such as air or water) surrounding the object and the sound waves produced in that fluid. The load (or pressure) of the air on the structure will also affect the ability of the structure to vibrate. That’s where COMSOL comes in, making such a coupling between the structural mechanics and acoustic aspects of an object easy to simulate and analyze.
One application where this acoustic-structural interaction analysis is applicable in music is in the design of a tuning fork. A tuning fork is used to tune instruments in an orchestra to a pitch of exactly 440 Hz, which is the note A above middle C, in musical terms. When a tuning fork is struck against an object or surface, its two prongs, or tines, vibrate at their resonant frequencies and create sound waves that should correspond exactly to 440 Hz. An incorrectly designed tuning fork would cause instruments tuned with the device to be out of tune with other instruments, creating unwanted clashes in the harmonies you hear during a concert.
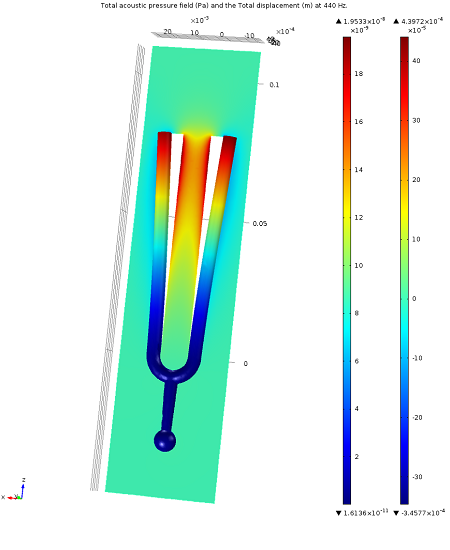
Vibrating tuning fork geometry showing the acoustic pressure field and displacement of the fork’s prongs.
Analysis of a Tuning Fork
Let’s take a look at an example of an analysis of a tuning fork in COMSOL (note that you can download this tuning fork model file below). This model has two basic steps of analysis:
- First, in Study 1 of the model, we analyze how the fundamental eigenfrequency of this particular shape of tuning fork changes as we vary the length of the prongs. We plot both the shape of the deformation of the fork as it vibrates, and we also plot the frequency the fork will naturally vibrate at when it is struck, based on the length of the prongs. You will see in this plot how the eigenfrequency drops as the prong length increases. The relationship between these two parameters is quite sensitive; an increase of only 1 mm in prong length corresponds to a decrease of about 10 Hz for the resonant frequency. This eigenfrequency vs. prong length plot below (left) shows us that the ideal prong length for this tuning fork is approximately 7.906 cm.
- Now that we have determined our desired prong length, we want to investigate the interaction between the acoustics and the structural components of the fork to analyze the sound that will be radiating from the tuning fork out to the orchestra. We use a Frequency Domain study type to see the characteristics of the sound produced for a harmonic structural load on a prong of the tuning fork that varies over frequency. From this analysis we are able to verify that the resonant frequency of this tuning fork is indeed at 440 Hz. This is depicted in the figure below (right). Note that only the relative levels are of interest here (their absolute values are inaudible), as we have simply applied a unit load in this example. We can also calculate the magnitude of the sound we would expect to hear from the tuning fork based on different magnitudes of applied structural loads. This study corresponds to finding the frequency response of the fork; that is, the Fourier components of the response. In practice, a tuning fork starts to vibrate when it is struck with another object, and from this object it receives an impulse consisting of several Fourier components. In this study we are also able to create plots of the radiation pattern of sound coming from the fork. This analysis gives us an accurate picture of how these two physics are working together to produce the tone heard by musicians while tuning their instruments in an orchestra.
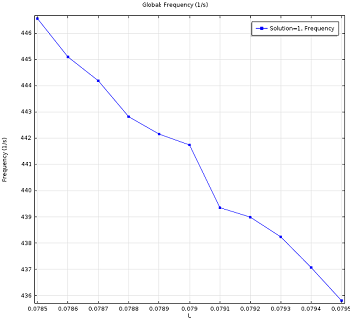
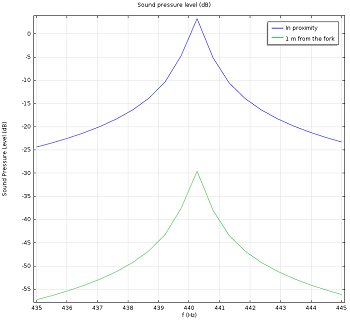
The left figure shows the fundamental vibrating frequency of the tuning fork as a function of the prong length L. The right figure depicts the sound pressure level measured in the proximity of the tuning fork (blue line) and measured at 1 m away from the fork (green line) at 440 Hz. Only the relative value is of interest as the fork is actuated by a unit load (right). Click to view larger images.
Theoretical Solutions Sometimes Come up Short
Note that a theoretical solution exists that relates the resonate frequency of an “ideal” tuning fork to the other parameters of the fork, such as the fork material’s Young’s modulus, the material’s density, the radius of the prong cross sections, and the length of the two prongs. However, this theoretical solution assumes that the prongs of the fork are perfect cantilever beams, where in reality the bending stiffness of the prongs increases near the base of the fork where the prongs meet. Therefore, you should use COMSOL Multiphysics to explicitly model applications like the tuning fork where the real device you want to model doesn’t match up perfectly with the assumptions made by known theoretical solutions.
We find in this model that using theory alone we would arrive at a tuning fork with prongs of length 7.8 cm, but our COMSOL model has shown us that the real length needed for this particular tuning fork design is 7.906 cm. If we would have designed this tuning fork with the theoretically-determined prong length, our tuning fork would create a tone at about 430 Hz, which is nearly a quartertone away from the desired note A at 440 Hz. This difference would be very noticeable to the average listener and would create quite an undesirable clash of harmonies within the orchestra.
Model Download
- Download the Tuning Fork with Acoustics model from the Model Gallery
- Or download the pure structural mechanics model of a the tuning fork geometry




Comments (0)