
We’ve blogged about how you can save time setting up your electromagnetic models by using symmetry, anti-symmetry, and periodic boundary conditions. Today, we’ll show you a model that takes advantage of axisymmetry — a conical horn antenna model.
Saving Time with a 2D Axisymmetric Model
Although it is possible to set up and solve a 3D model of a conical horn antenna, such a model would require a relatively large amount of computational resources to solve. We can solve for the electromagnetic fields much more quickly by exploiting the symmetry of the structure. Because we are dealing with a cone, our model is structurally symmetric around its axis, i.e., it’s axisymmetric.
Now, although the structure is axisymmetric, the electromagnetic fields will have some variation around the azimuth of the axis, that is, the fields have an azimuthal variation. The RF Module and the Wave Optics Module allow you to model axisymmetric structures with different azimuthal mode numbers.
We can exploit this feature; by building a 2D axisymmetric model and solving for several different azimuthal mode numbers, we can build a model that solves much quicker and uses less memory than a full 3D model. I like the sound of that. But first, a quick note on horn antennas.
General Note on Horn Antennas
There are various types of horn antennas in terms of both overall shape and pattern of the inside. These attributes determine the antenna’s beam profile, bandwidth, and cross-polarization.
Cross-polarization means that the electromagnetic fields are polarized opposite to what is intended. For example, we want the fields to be polarized vertically, but they are instead polarized horizontally.
The funnel part of the antenna is connected to a waveguide, which feeds electromagnetic waves into the antenna. The shape of the horn will dictate what application it’s suited for. For example, sectoral horns (labeled b and c in the image below) are typically used for wide search radar antennas.
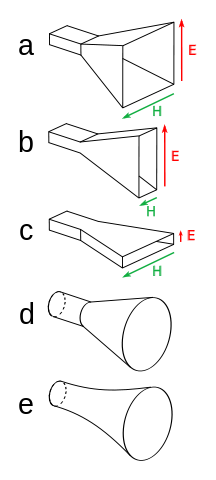
Various horn antenna shapes: a) pyramidal; b) sectoral, E-plane; c) sectoral, H-plane; d) conical; e) exponential. “Horn antenna types” by Chetvorno — Own work. Licensed under Creative Commons Zero, Public Domain Dedication via Wikimedia Commons.
Corrugated Conical Horn Antenna Model
The antenna in our case is both shaped like a cone (labeled d in the image above) and has a corrugated surface inside; it’s a corrugated conical horn antenna fed by a circular waveguide. The waveguide passes the excited TE mode through the corrugated funnel, which, in turn, generates a TM mode. Due to the corrugated surface throughout the cone, the modes are mixed, leading to a lower cross-polarization at the aperture than the original excited TE mode.
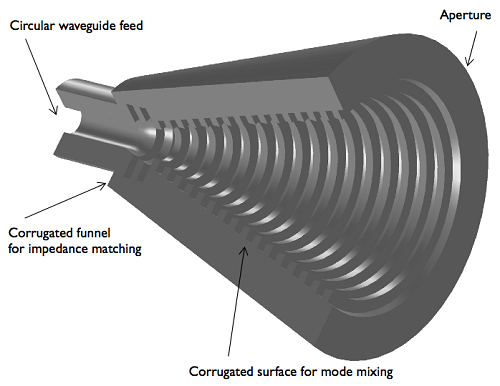
Conical horn antenna: A visualization in 3D based on a 2D axisymmetric model. The waveguide feeds the antenna with the TE1m mode (m = ±1), which mixes with the TM1m mode as it propagates through the antenna.
Above, I mentioned what cross-polarization is, but why would we want to reduce it? Well, if we have a lot of cross-polarization, our signal may interfere with other channels nearby, if they have alternating vertical and horizontal polarization. We wouldn’t want that.
Investigating Cross-Polarization in the Horn Antenna
To investigate the cross-polarization, we can use COMSOL Multiphysics and the RF Module to set up a model. As we learned earlier, we can save time by solving this as a 2D axisymmetric model instead of in 3D. We can do that by using the Electromagnetic Waves, Frequency Domain interface.
I will skip over the step-by-step model set-up and head straight to the fun stuff — the results. If you want to reproduce the plots shown here, feel free to download the model documentation and MPH file from the Model Gallery.
First, we can see what the directive beam pattern of the antenna is:
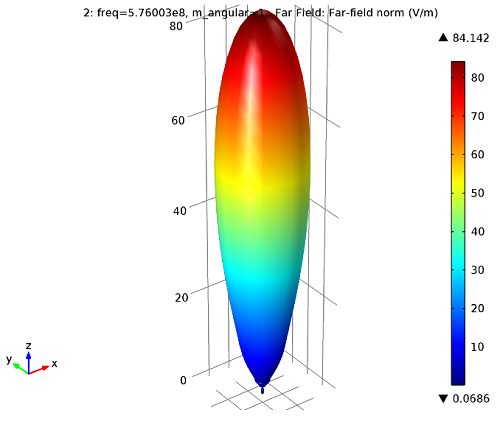
Far-field plot: The directive beam pattern of the antenna.
Next, we can analyze the electric field at the antenna’s entrance and exit. By solving the model for both m = +1 and m = -1, we can compare the linear polarization in the x– and y-direction at the exit.
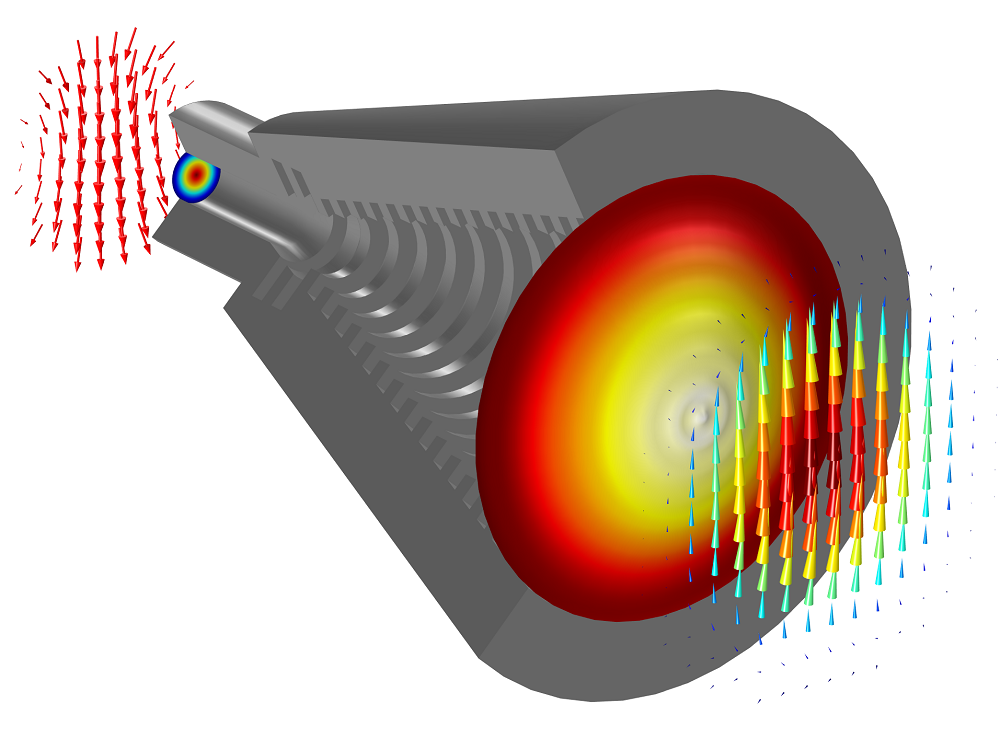
Electric field at the entrance and exit of the antenna for the linear superposition of m = +1 and m = -1.
At the waveguide feed, the field is mostly in the x-direction, but not linearly polarized. At the aperture, the field is very nearly linearly polarized. To quantify the polarization in both directions, we can evaluate the integral of the absolute value of each field component over the conical horn antenna’s entrance and exit. Doing so, we’ll find that the ratio is roughly 5:1 at the entrance and about 40:1 at the exit. In other words, we have reduced the cross-polarization by approximately a factor of 8.




Comments (0)